Гармония золотых пропорций 7 страница

Центр матрицы 1'	Центр матрицы 2'
1,414 1,272	2 1,618
10,899	1 0,809

Основу структуры русской матрицы 3 составляет двойная крестовая последовательность записи чисел, при которой центр матрицы образует базисная 1 (единица), и в одной с ней строке находятся цифры горизонтального ряда, а перпендикулярно ей вертикальный (базисный) ряд, формирующий числовое поле матрицы, начинающийся с рационального или иррационального числа. По диагонали через 1 снизу вверх слева направо - диагональный ряд, начинающийся либо с золотого числа Ф либо с Ф в степени, либо степень от Ф. Числовое поле матрицы распространяется в бесконечность во все направления. Плоскую матрицу формируют три числа (объемную - четыре):

базисная 1, находящаяся в центре матрицы и наличествующая во всех матрицах, иногда в виртуальном виде;

золотое число, следующее по диагонали от1, как в виде Ф, так и Ф в степени или степень от него;

рациональное или иррациональное число над 1 (кроме Ф).

Плоскость числового поля матрицы образуется как бы невидимыми квадратиками-клетками, в которые вписываются числа. Приведем фрагмент русской матрицы 3:

Матрица 3

9,609	8,643	7,774	6,992	6,289	5,567	5,088	4,576	4,116	3,702	3,330
6,795	6,111	5,497	4,944	4,447	4,000	3,598	3,236	2,911	2,618	2,355
4,804	4,31	3,887	3,496	3,145	2,828	2,544	2,288	2,058	1,851	1,665
3,397	3,056	2,748	2,472	2,224	2,000	1,799	1,618	1,455	1,309	1,177
2,402	2,161	1,943	1,748	1,572	1,414	1,272	1,144	1,029	0,925	0,832
1,699	1,528	1,374	1,236	1,112	1,000	0,899	0,809	0,727	0,654	0,588
1,201	1,080	0,972	0,874	0,786	0,707	0,636	0,572	0,514	0,463	0,416
0,849	0,769	0,687	0,618	0,535	0,500	0,449	0,404	0,364	0,327	0,294
0,601	0,540	0,487	0,437	0,399	0,354	0,318	0,286	0,257	0,231	0,208
0,425	0,382	0,344	0,309	0,278	0,250	0,225	0,202	0,182	0,164	0,147
0,300	0,270	0,243	0,218	0,196	0,177	0,159	0,143	0,129	0,116	0,104

Матрица 3, как и другие русские матрицы, имеет объемную слоистую структуру. Так, числа 1,414..., 1,272..., 1,144... и т.д., образует ряд чисел, называемый также слоем, и заполняют слоями не только клетки вертикальной, видимой нами плоскости, но и те, которые существуют за ними и за данной плоскостью не наблюдаемы. За ними находятся пропорциональные им числа другого слоя-плоскости, еще дальше третьего и так далее в бесконечность.

Перед ними, т.е. в нашу сторону, виртуально, продолжается такое же бесконечное поле взаимосвязанных и связанных с числами плоскости матрицы 3 числовых плоскостей. Их можно представить и по-другому, проведя через базисную 1 и другие числа горизонтального ряда горизонтальную плоскость-слой. Эта плоскость будет разграфлена такими же клетками, как и вертикальная плоскость и в каждой клетке будут находиться числа, пропорциональные числам вертикального слоя и Ф. То же произойдет и с горизонтальной плоскостью проведенной через числа 1,414, 1,272, 1,144 и т.д.

В результате клетки каждого слоя объемной матрицы как бы образуют единичные кубические объемы-ячейки, содержащие по одному иррациональному и редко рациональному числу. И все числа бесконечного объема матрицы оказываются связанными между собой определенной числовой зависимостью, а следовательно, базисная единица является невидимой составляющей каждого числа. Далее речь пойдет в основном о вертикальных слоях матриц. Отмечу основные особенности структуры русских матриц:

основу каждой матрицы составляет базисная 1;

плоскость матрицы имеет двойную крестовую структуру расположения чисел с центром - базисной 1(фрагмент матрицы 3);

числовое поле матрицы объемно и бесконечно во все стороны;

все члены любой части числового поля матрицы индивидуальны, иррациональны, взаимосвязаны, но каждое число не равно никакому другому числу и по другую сторону базисной 1, оно имеет свой обратный аналог;

числовое поле плоской матрицы формируется тройкой чисел, а объемной матрицы - четверкой чисел. Количественные величины этих четырех чисел позволяет образовывать бесчисленное количество матриц со свойствами золотых пропорций;

базисная диагональ с числом, пропорциональным Ф, образуется только по структуре аналогичной русскому или египетскому ряду;

крестовая форма между столбцом и строкой матрицы обусловливает возможность использовать их как координатные системы для нахождения места любого числа ее множеств по показателю степени строки или столбца;

базисный ряд может начинаться с любого числа как рационального, так и иррационального, но не может начинаться с Ф.

То, что матрица 3 имеет сакральную структуру, не приходится даже доказывать. Она – формальное математическое целое. Она, как и все матрицы аналогичной структуры, базируется на том же русском числовом ряде и потому включает в себя сакральную структуру. В центре матрицы - базисная 1, на которой, с любой стороны, заканчивается одно качество числового ряда и начинается другое. Все бесконечное количество чисел поля аналогичных матриц связано друг с другом через базисную 1 и, следовательно, имеет частичку ее качества. (Все, опять же, по Библии.) Все они связаны всеобщей инвариантной зависимостью, составляя взаимообусловленное числовое «население» матриц. И можно констатировать: как текст Нового Завета пронизан Божественностью Христа, его учением, и жизнью апостолов, так и все содержание динамической геометрии базируется на вещественности мира, на системе 1\12, всеобщем движении и качественном изменении (деформации). И так же как жизнь Христа доказывает существование Бога-Отца, так и структура и взаимосвязи русской матрицы подтверждают то же в опосредственной форме, становясь математическим подтверждением существования Бога.

Но вернемся к числовому полю матриц. Перед нами как бы необъятно расширенный вариант русского ряда, структура которого обладает множеством новых свойств. Вот некоторые из них.

Все последовательные тройки диагональных чисел матрицы 3 повторяют свойство русского ряда «плести гирлянду» подобных треугольников.

Если в матрице 3 все числа каждой клетки возвести в квадрат, то получим матрицу 4, главная диагональ которой структурирована египетским рядом.

Тот же результат достигается и в том случае, если, начиная от базисной 1, и по горизонтали и по вертикали вычеркиваем через один столбец слои, начиная с числа 1,272..., и через строку, начиная с 1,414..., и оставшееся поле матрицы «сплачиваем», сдвигая слои к базисной 1 (матрица 4). Если же вычеркивать слои и столбцы через строку, начиная с крестовины базисной 1, и сплотить оставшееся поле матрицы, то получим матрицу, обладающую теми же свойствами, но с виртуальной 1.

Последовательность диагональных чисел матрицы 4 после сплочения из матрицы 3, «теряет» способность образовывать «гирлянды» треугольников, но у них ярко проявляется достаточно скрытая в других формах матриц качество матричной «вязи», заключающееся в возможности получения методом сложения или вычитания из одних чисел других, находящихся в том же поле.

Матрица 4

35,42	28,66	23,08	18,67	15,11	12,22	9,888	8,00	6,472	5,236	4,236
17,71	14,33	11,54	9,337	7,554	6,114	4,944	4,00	3,236	2,618	2,118
8,854	7,164	5,771	4,668	3,777	3,058	2,472	2,00	1,618	1,309	1,059
4,427	3,582	2,885	2,334	1,888	1,528	1,236	1,00	0,809	0,654	0,529
2,214	1,791	1,449	1,167	0,944	0,764	0,618	0,50	0,404	0,327	0,264
1,107	0,895	0,721	0,583	0,472	0,382	0,309	0,25	0,202	0,163	0,132
0,553	0,448	0,361	0,292	0,236	0,191	0,154	0,125	0,101	0,082	0,066
0,277	0,224	0,180	0,146	0,118	0,095	0,077	0,062	0.051	0,041	0,033
0,138	0,112	0,090	0,073	0,059	0,048	0,039	0,031	0,025	0,020	0,016
0,069	0,056	0,045	0,036	0,029	0,024	0,019	0,016	0,013	0,010	0,008
0,034		0,022	0,018	0,014	0,011	0,009	0,007	0,006	0,005	0,004

Приведем несколько примеров матричной вязи, опираясь на известное на сегодня правило сложения и вычитания Фибоначчи. Напомним его и покажем еще некоторые из них на примере числового поля, окружающего базисную 1, отметив, что в примерах она не принимается за базисную, поскольку по той же конфигурации могут складываться любые числа поля [23].

Получаем 1, соблюдая правило Фибоначчи, когда сумма двух последовательных нижних чисел по диагонали слева направо снизу вверх равна верхнему числу. Те же числа находятся при диагональном вычитании из верхнего любого из двух нижних чисел:

0,382 + 0,618 = 1.

Складывая по диагонали вверх три числа подряд, получаем в результате число, стоящее в таблице над последним слагаемым:

0,382 + 0,618 + 1 = 2.

Берем число 0,191, стоящее в таблице под 0,382. И складываем его методом единицы (движение по полю матрицы как бы выписывает единицу) с числом 0,809, находящимся от него через два числа вверх, вправо по диагонали. Результат сложения находится слева от числа 0,809:

0,191 + 0,809 = 1.

Используем метод двойного хода “шахматного коня”: с поля 0,236 “переступаем” через число 0,472, а от числа 0,944 движемся направо к 0,764 и складываем его с первым:

0,236 + 0,764 = 1.

“Шаги” через числа могут быть и более длинными. Например, возьмем число 0,056 на главной диагонали. Через пять чисел вверх на числе 1,783 повернем вправо и через два числа найдем 0,944. Сложим их, сделав один шаг наверх и два вправо, находим 1:

0,056 + 0,944 = 1.

Или, по тем же правилам, от числа 0,118 пройдем к числу 2 и, сделав ход вверх и два вправо, имеем:

0,118 + 2 = 2,118.

Или по главной диагонали:

0,0213 + 0,0344 + 0,0902 + 0,236 + 0,618 = 1.

Количество слагаемых может возрастать. Например, суммируя от 0,146 по главной диагонали, двигаясь через число 0,382, к 1 и от него, тоже через число влево, можно получить результат 1,528:

0,146 + 0,382 + 1 = 1,528,

оставаться последовательным:

0,146 + 0,382 + 0,472 = 1,

становиться фрактальным:

0,1803 + 0,236 + 0,5836 = 1,

или образовывать различные комбинации из них:

0,08514 + 0,1114 + 0,146 + 0,2755 + 0,382 = 1 и т.д.

Количество примеров, и не только сложения, но и всех действий арифметики, можно множить и множить. Правила их использования относятся ко всем числам поля и в совокупности со степенными числовыми рядами образуют матричную «вязь», охватывающую все числовое поле как матрицы 3, так и матрицы 4. Матричная вязь есть следствие отдельности каждого элемента числового поля, и отображает принадлежность его к числовому полю как к целому. Именно матричная «вязь» обеспечивает корректность операций между золотыми числами полей этих матриц.

Русскую матрицу можно образовать, заполнив ее не иррациональными числами, а их отображениями в угловых единицах (в градусах). В такой матрице 5 необычная система углов представляет, по-видимому, некую величину поворота относительно базисной единицы. Хотя не исключена иная, еще не выявленная взаимосвязь.Немаловажно так же и то, что в матрице 5 наряду со значениями целых и дробных углов, например, 30^о, 60^о, 72^о, проявляется число p с точностью как минимум до десятого знака (как cos 72^o). И можно показать, что между золотым числом и коэффициентом p имеется взаимосвязь, отображаемая формулой:

1/Ф = (1 - Ö5)/2 = 2 cos72^о = 1∕2 sin(90^о − 36^о)

Матрица 5

15,11	12,22	9,888	8,00	6,472	5,236	4,236
7,554	6,114	4,944	4,00	3,236	2,618	2,118
3,777	3,058	2,472	2.00	1,618
			90о 0¢	36о 0¢	49о 9¢	58о 4¢
19о 16¢	40о 11¢	51о 50¢	60о 0¢	66о 10¢	70о 55¢	74о 41,5¢
61о 50¢	67о 32,5¢	72о 0¢	75о 31¢	78о 24¢	80о 37¢	82о 25¢
76о 21¢	78о 59¢	81о 8,5¢	82о 49¢	84о 12¢	85о 18¢	86о 13¢

Приведем еще один вариант матрицы, связанный как с древнерусскими саженями, так и с размерностью физических уравнений. Начнем с саженей. Оказалось, что длины древних саженей были извлечены из числового поля матрицы, в которой число, задающее шаг базисного столбца, является малой темперированной секундой музыкального ряда, равной 1,05945... и получается извлечением корня двенадцатой степени из 2, главная диагональ кратна Ф, а сама матрица имеет гармоническую структуру, относящуюся не только к музыке, но и самым непосредственным образом к физике. Числа базисного ряда гармонической матрицы 6 являются качественными коэффициентами физической размерности (КФР) свойств тел, составляя основу теории размерности. КФР позволяет принципиально по-иному подходить к этой теории и к формализации физических уравнений (ниже метод КФР будет разобран подробнее). Приведем фрагмент матрицы 6.

Следует отметить, что корень двенадцатой степени из 2 появился не случайно. Он следствие перенесения на базисный столбец рациональных чисел отображающих деление динамического отрезка на 12 физически одинаковых частей. То есть здесь имеет место почисловое отражение русского ряда на вертикальный базисный ряд матрицы.

В матрице 6 древнерусские сажени располагаются, начиная с 350-й строки, под базисной 1 и заканчиваются 418 строкой. А по столбцам начиная с 60-й и заканчивая 70 столбцом [23]. Отмечу, что величина саженей подобрана таким образом, что получается ступенчатая последовательность расположения значащих чисел (их длин с точностью до четвертого знака), которая обеспечивает, посредством 12 последовательных умножений на 1,05946, удвоение каждого числа. Это очень удивительная структура, определяющая некую «иерархически соподчиненную» взаимосвязь чисел матрицы

6. В ней величина длин саженей оказывалась «выше» по значимости, чем расположенные под ними 10 «промежуточных» чисел. Эти промежуточные числа в столбцах можно «убрать», проведя операцию «свертывания» промежуточных чисел и подтягивания в одну строку оставшихся значащих чисел. Последнее не меняя структуру матрицы, увеличивает шаг базисного столбца и изменяет ее числовое поле, а, следовательно, и ранг чисел, переводя их из «соподчиненных» в смежные, убирая физическую гармонику базисного ряда, а с ним «укрывая» и качественную обусловленность взаимосвязи всех физических свойств.

Матрица 6

0,1670	0,2550	0,3895	0,5949	0,9085	1,387	2,119	3,236	4,942
0,1576	0,2407	0,3676	0,5615	0,8575	1,309	2,000	3,054	4,665
0,1488	0,2272	0,3470	0,5300	0,8094	1,236	1,888	2,883	4,403
0,1404	0,2146	0,3275	0,5002	0,7639	1,167	1,782	2,721	4,156
0,1325	0,2024	0,3091	0,4721	0,7211	1,101	1,682	2,568	3,923
0,1251	0,1911	0,2918	0,4456	0,6806	1,039	1,587	2,424	3,703
0,1181	0,1804	0,2754	0,4296	0,6324	0,981	1,498	2,288	3,496
0,1114	0,1702	0,2599	0,3970	0,6063	0,926	1,414	2,160	3,296
0,1052	0,1607	0,2464	0,3747	0,5723	0,874	1,335	2,039	3,113
0,0993	0,1516	0,2316	0,3537	0,5402	0,825	1,260	1,924	2,939
0,0937	0,1431	0,2186	0,3339	0,5099	0,779	1,189	1,816	2,774
0,0885	0,1361	0,2063	0,3151	0,4812	0,736	1,122	1,714	2,618
0,0835	0,1275	0,1948	0,2974	0,4542	0,694	1,059	1,618	2,471
0,0788	0,1204	0,1838	0,2807	0,4282	0,655	1,000	1,527	2,332
0,0744	0,1136	0,1735	0,2650	0,4047	0,618	0,944	1,441	2,201

Выбор размеров древнерусских саженей оказался далеко не случайным, хотя таким он кажется на первый взгляд. Если, начиная с 1 сосчитать количество строк - 351 до численного размера наименьшей из саженей – 1,345 м. и, возвести основание 1,05946... в степень 351, то получим, с точностью до 0,1% модуль радиуса земного шара – 6384,5 км. Более точное целое число получается, если разделить радиус Земли, равный 6378 км, на длину царской сажени 1,974 м или на ту же меньшую сажень 1,345 м. Результат поразителен для чисел из четырех значащих цифр. Получаем целые до шестого знака числа: 323100 в первом случае и 474200. Эта интересная «случайность» обусловливает объектам, возводимым по древней методике получение объемов сооружений, квантованных пропорционально структуре Земли (подробнее [23]).

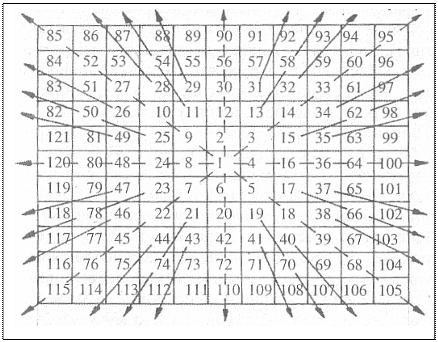
И, наконец, еще одна важная для понимания естественной структуры реального пространства особенность формы русской матрицы. Из всех клеток-ячеек матрицы уберем числа, оставив только базисную 1, проведем нумерацию их, начиная с этой 1, и поставим в верхнюю клетку цифру 2. Далее двигаясь по часовой стрелке, получим удивительную и странную полуматрицу (матрица 7), сводящую динамическую геометрию с геометрией золотых пропорций и отображающую их квантованное единство.

Рассмотрим фрагмент этой полуматрицы из 121-й клетки-ячейки.

Матрица 7.

Образующаяся полуматрица интересна сама по себе и заслуживает отдельного исследования. Таблица названа полуматрицей, поскольку в нее входят и взаимосвязанные и степенные числа, изменяющиеся на одну и ту же величину.

Всеобщая связь между каждым числом, похоже, отсутствует. Например, все клетки базисного «креста» горизонтального и вертикального слоев заполнены четными числами, что свидетельствует о качественном отличии базисной 1 от других чисел матрицы. Но главное достоинство полуматрицы в том, что на ее примере можно наглядно демонстрировать образование лучей-спиц, но не снаружи внутри, как на рис. 33, а изнутри наружу. Иначе говоря, структура этих двух моделей аналогична. И аналогия эта, во-первых, подтверждает единство геометрий, а во-вторых, позволяет проследить процесс образования ячеистой системы лучеиспускания на плоскости. Процесс сохраняется и при построении объемной ячеистой структуры (в ней клетки превращаются в кубики-ячейки).

Итак, первые четыре луча 2-90; 4-100; 6-110; 8-120 исходят от границ базисной ячейки и образуют крест. В своем движении наружу они «засвечивают» все встречающиеся ячейки. Следующие четыре луча (9-85; 3-95; 5-105; 7-115) исходящие из центров нечетных ячеек, «засвечивают» все диагональные ячейки, образуя диагональный крест. Далее количество ячеек удваивается, и лучи испускают ячейки 11, 13, 15, 17, 19, 21, 23, 25. Эти ячейки с нечетной нумерацией по очертанию начинают приближаться к окружности, образуя фигуру наподобие кольца (сферы в объеме). Испускаемые ими лучи двигаются наружу как бы от центра базиса «засвечивая» ячейки через одну. Лучи исходят из смежных, относительно центральной единицы, ячеек в противоположных направлениях. Например, луч из ячейки 11, пропуская одно кольцо ячеек, «засвечивает» 54, далее 129 и т.д. Противоположный луч из ячейки 19 через ячейку 70, 153 и т.д.

При переходе от плоской матрицы к объемной, эффект сферы лучеиспускания усиливается и с каждым новым слоем ячеек объем сферы возрастает, а плотность исходящих лучей превращается в некоторый аналог «ежика» следов, входящих в сферу как на рис. 33.

Уже говорилось,что символом непроявленного «движения» чисел в ячейках может считаться образование числового поля в матрицах неопределенными числами. Неопределенными потому, что их точное цифровое значение неизвестно. Невычисляемо, а следовательно, и непостоянно, подвижно, причем самоподвижно.

Теперь, имея представление о русских матрицах и опираясь на их числовые поля, попробуем рассмотреть возможность построения квантованной физической геометрии на основе числовых полей матриц 2 и 4 и той пространственной зависимости, которая скрывается за ними.

Еще раз вернемся к уравнению (3.12) и отметим странное заблуждение, чуть ли не эйфорию, охватившую ученых после введения Минковским времени и скорости света в уравнение системы взаимнопересекающихся плоскостей евклидовой геометрии. Получившемуся квадратичному уравнению

0 = c² t² − x² − y² − z², (5.6)

качественно не изменившему евклидовости пространства, поскольку в квадратичном уравнении Евклида один размерный индекс был заменен на другой и только, Минковский, без каких либо оснований, приписал ранг четвертого измерения. То есть нового качественного состояния - четырехмерной объемности, а, следовательно, и неевклидовости.

И, как это ни удивительно, но сначала физики, а затем и математики поверили в «четырехмерность» полученного квадратичного уравнения и, более того, стали получать аналогичные «пятимерные» (Калуца), «шестимерные»..., «одинадцатимерные»..., «двадцатипяти...» [33] и т.д. мерные квадратичные уравнения. Как то забылось, что х² - есть плоскость (не объем), разделяющая (а не образующая) пространство на две части, а координата х - след-линия пересечения этой плоскости с другой ортогональной ей, у² - тоже плоскость, но в ином ортогональном направлении. И, наконец, z² - такая же плоскость, ортогональная двум другим. И объем не образуется этими тремя взаимнонезависимыми, не связанными между собой плоскостями, а заключается между ними. И в этом объеме с²t² - еще одна плоскость, проходящая ортогонально одной из них в стык двух других.

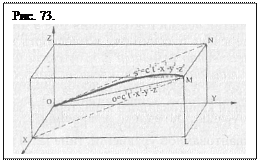
Введение в уравнение (3.9) неравенства и дополнительной координаты s не меняет качества уравнения, поскольку s² - тоже плоскость неопределенной ортогональности. или искривленная линия, если считать, что (5.6) аналог (3.12) С появлением этой индексации в евклидовой геометрии не изменилось ничего, кроме названия. Модель решения уравнения (3.12) получена Ф. Канаревым [34] и показана на рисунке 47, на котором путь от О к М отмечен и по уравнению (3.11) и по уравнению (5.6). Разница понятна и без пояснения.

Что касается с²×t², то его появление в уравнении (3.12) нарушило пространственную соразмерность параметров х, у, z и потому превратило однозначность решения уравнения Пифагора в многозначность даже без учета того, что время как естественная категория в природе отсутствует [2], к тому же плотность евклидова пространства изотропна, а матричного пространства - анизотропна. Именно «выпрямляя» анизотропность, искривляют пространство члены уравнения (3.12) в «знаменитой» теории ОТО. И из решения уравнения (3.12) могут быть получены как корректные (случайно), так и полностью некорректные (регулярно) результаты.

Но элементы псевдо-евклидовой геометрии русского ряда золотой пропорции (3.9) совер- шенно иначе «реагируют» на введение других членов. Они не могут содержать «лишних» членов и форма неравенства (3.10¢) для них невозможна. Неравенство предполагает расширение количества членов, а ряд такого расширения не допускает. Поэтому неравенство (3.10¢) «выводит» взаимосвязи между членами (3.10) за рамки отдельного ряда в плоскость матрицы, когда у_о оказывается не равной z: у_о ¹ z, допуская введение в (3.10) новых членов, первым из которых и становится s².

Таким образом, заменив равенство в (3.10) на неравенство и введя равноправный член s² в уравнение (3.12), математики не в евклидовой, а в квантованной геометрии произвели не одно действие, а два (так же как и при делении в крайнем и среднем отношении). Превратили «самостоятельный» ряд в диагональ матрицы 1 переведя русский ряд в плоскость матрицы. Качественно изменив, таким образом, форму связи членов уравнения (3.9) с линейной, между членами одного ряда, на плоскостную − между числами поля всей матрицы, но не изменив квантованного характера их зависимости.