Теоретическое введение. Значимость решения задачи по определению коэффициентов активности сложно

Значимость решения задачи по определению коэффициентов активности сложно переоценить, т.к. используя значения активности можно решать широчайший спектр прикладных задач в металлургии. К таким задачам можно отнести:

1. Определение прочности оксидов исходя из значения кислородного потенциала по формуле с последующим определением безокислительных условий обжига из условий равенства кислородного потенциала атмосферы и системы Me_xO_y - Me:

p₀ (Me_xO_y) = DG_(MexOy) + (2 / y) * R*T*ln a_(MexOy) - (2*x / y)*R*T*ln a_[Me], (1)

где: p₀ (Me_xO_y) – кислородный потенциал в системе Me_xO_y - Me

DG_(MexOy) - изменение энергии Гиббса для данного оксида

R – универсальная газовая постоянная (8,31)

T – температура, К

a_(MexOy) - активность оксида в шлаке

a_[Me] – активность металла в металлической фазе

2. Определение температуры начала восстановления оксида твердым углеродом по формуле:

Т_н.в. = (М₂ – М₁) / ( N₁ – N₂ + 38,81*( 1/y * ln a_(MexOy) – x/y* ln a_[Me] – lg P)), (2)

где: М₂ , М₁ , N₁ , N₂ - эмпирические коэффициенты в уравнении Гиббса для реакции окисления металла и углерода

P – давление в системе, ат

3. Распределение химических элементов между металлургическими фазами – металлом, шлаком и газом в окислительных (мартен, конвертор) или восстановительных (домна, ферросплавная печь) условиях. Например, распределение марганца между металлом и шлаком, которое можно найти по уравнению:

- 12200 / T + 9,56 = ln a_[Mn] * P_CO / a_[c] * a_(MnO), (3)

где: a_[Mn] – активность марганца в металлическом расплаве

P_CO – парциальное давление СО, Па

a_[c] – активность углерода

a_(MnO) – активность оксида марганца в шлаке

Для определения активности компонента в растворе пользуются уравнением Нернста, которое связывает активность и потенциал электрода в электрохимических процессах. Согласно уравнению:

Е = Е⁰ + (R*T / n*F) * ln (a_Men+ / a_[Me]), (4)

где: Е⁰ – стандартный потенциал окисления-восстановления, В

R – универсальная газовая постоянная (8,31)

T – температура, К

n – число электронов, участвующих в реакции

F – постоянная Фарадея = 96500

a_Men+ - активность иона в водном растворе

a _Me] – активность металла в сплаве

При условии протекания в системе реакции:

[Ме] = Meⁿ⁺ + n e ^– , (5)

Предположим, что имеется два электрода изготовленных из материалов с различным значением электродного потенциала. Например, пластины из цинка и из меди погружены в раствор сульфата меди и соединены внешней электрической цепью. Пластина из цинка будет подвергаться окислению, а медь из раствора будет осаждаться на медной пластине. Во внешней цепи возникнет ЭДС. В стандартных условиях Е⁰ (меди) = 0,34В, Е⁰ (цинка) = - 0,763 В. Учитывая, что ЭДС такого гальванического элемента определяется уравнением:

DЕ⁰ = Е⁰ (меди) - Е⁰ (цинка) (6)

такой элемент будет давать напряжение 0,34 + 0,763 = 1,103В.

Если пластины изготовлены из химически чистых элементов, то активность a_[Me] – будет равна 1. В этом случае ЭДС гальванической пары будет определяться только активностью иона a_Men+. Необходимо стараться завершить исследование до того как концентрация цинка в растворе достигнет сколь либо значительной величины. Иначе ЭДС элемента будет определяться активностями двух ионов согласно уравнению:

DЕ = DЕ⁰ + (R*T / n*F) * ln (a_Сu2+ / a_Zn2+), (7)

Таким образом, мы получим одно уравнение с двумя неизвестными даже в том случае, если в качестве электродов будут использоваться пластины из чистых металлов.

Никогда не следует забывать о возможности явления поляризации электрода. Оно может существенно исказить результаты эксперимента, т.к. оно способно изменить потенциал электрода в соответствии с формулами:

Е_к = Е⁰_к + Е^пер_к, (8)

Е_a = Е⁰_a + Е^пер_a, (9)

где: Е^пер_{к, а} – перенапряжение реакции окисления-восстановления на катоде, аноде, В

Явление перенапряжения может быть вызвано двумя причинами:

1. Диффузионная поляризация. Она вызвана не равномерностью концентрации в основном объеме электролита – а_{Сu2+ (объем)} и в тонком слое электролита прилегающего к поверхности - а_{Сu2+ (поверх)}. Как правило, активность (концентрация) у поверхности электрода значительно ниже, чем в объеме. Это объясняется низкой турбулизацией жидкости у любой границы раздела фаз жидкость – твердое тело в принципе и массоперенос в этой области за счет диффузии процесс замедлен переносом массы через границу раздела фаз. Уменьшить это явление можно путем активного перемешивания электролита, что собственно и делается в промышленности. Величина перенапряжения рассчитывается по формуле:

Е^пер_к = (R*T / F) * ln (a_{Men+ (поверх)} / a_{Men+ (объем)}) (10)

2. Электрохимическая поляризация. Она вызвана не равномерностью распределения электрического заряда. Замедлен перенос заряда через границу раздела фаз. Это явление вызывается чрезмерной плотностью тока (отношением силы тока к площади поверхности электрода), протекающего во внешней цепи. Снизить влияние этого эффекта можно изготовлением электродов как можно большего размера. Максимально допустимые плотности тока трудно рассчитать теоретически. Для каждого конкретного электролита их подбирают опытным путем. Величина перенапряжения рассчитывается по формуле Тафеля:

Е^пер_к = а – b*lg I, (11)

где: а, b – эмпирические коэффициенты

I – плотность тока, А / см²

После того как изучена зависимость активности от концентрации ионов в растворе можно рассчитать коэффициенты активности исходя из классической формулы:

а = g * x, (12)

где: g - коэффициент активности

x – мольная доля

Примерная зависимость представлена на рисунке 1.

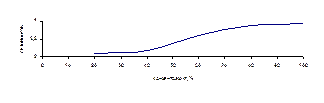
Рисунок 1 Зависимость активности компонента раствора от его концентрации.

Когда эта зависимость получена, выбирается концентрация, при которой наиболее удобно проведение эксперимента и тогда один из электродов (для рассмотренной пары медный) изготавливается из сплава меди и материала второго электрода. Поскольку известна активность ионов, то теперь активность меди в расплаве может быть рассчитана по уравнению 4.

Задачи исследования.

Освоить технику и методику определения коэффициентов активности в водных растворах и металлических расплавах методом ЭДС. Определение коэффициента активности и активности в ряде электролитов промышленного значения.