Криволинейные интегралы первого типа
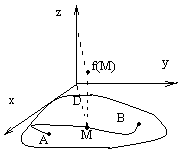 Рис. 15 Рис. 15 | Пусть в некоторой области D дана спрямляемая, гладкая кривая 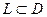 с началом в точке A и концом в точке B (рис. 15) и вдоль этой кривой определена функция z = f(x,y), т.е. каждой точке М кривой поставлено в соответствие определенное значение функции f(M). Разобьем кривую L произвольным образом на n частей точками с началом в точке A и концом в точке B (рис. 15) и вдоль этой кривой определена функция z = f(x,y), т.е. каждой точке М кривой поставлено в соответствие определенное значение функции f(M). Разобьем кривую L произвольным образом на n частей точками 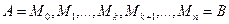 . . |
На каждой из частичных дуг 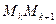 , длины которых обозначим
, длины которых обозначим 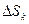 , выберем также произвольным образом по одной точке
, выберем также произвольным образом по одной точке 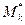 и вычислим значение функции в каждой из этих точек f(
и вычислим значение функции в каждой из этих точек f( 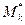 )=f(xk,yk). Составим сумму
)=f(xk,yk). Составим сумму 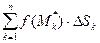 , которая называется интегральной суммой для функции f(x,y) вдоль кривой L. Обозначим наибольшую из длин частичных дуг
, которая называется интегральной суммой для функции f(x,y) вдоль кривой L. Обозначим наибольшую из длин частичных дуг 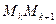 через λ:
через λ: 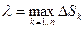 .
.
| Определение. | Если существует предел интегральных сумм при 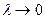 , который не зависит ни от способа разбиения кривой L на частичные дуги, ни от выбора точек , который не зависит ни от способа разбиения кривой L на частичные дуги, ни от выбора точек 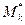 , то он называется криволинейным интегралом первого типа от функции f(x,y) по кривой L и обозначается: , то он называется криволинейным интегралом первого типа от функции f(x,y) по кривой L и обозначается: |
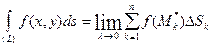 .
.
Иначе этот интеграл называют криволинейным интегралом по длине дуги.
Замечания.
- Величина криволинейного интеграла первого типа не зависит от направления интегрирования, т.е.
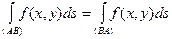 .
.
- Если дугу АВ разбить точкой С на две дуги АС и ВС, то
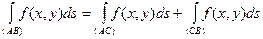 .
.
3. Геометрический смысл: криволинейный интеграл 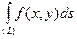 при
при 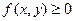 численно равен площади участка цилиндрической поверхности с образующей, параллельной оси Oz. Снизу этот участок ограничен контуром интегрирования (L), а сверху – кривой, изображающей подынтегральную функцию f(x,y).
численно равен площади участка цилиндрической поверхности с образующей, параллельной оси Oz. Снизу этот участок ограничен контуром интегрирования (L), а сверху – кривой, изображающей подынтегральную функцию f(x,y).
Вычисление криволинейных интегралов первого типа.
Криволинейный интеграл первого типа можно преобразовать к обыкновенному определенному интегралу. Пусть f(x,y) непрерывна вдоль кривой (L).
- Если кривая (L) – график непрерывно дифференцируемой функции y=g(x) на сегменте [a,b], где a<b, то
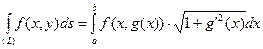 (*)
(*)
- Если кусочно-гладкая кривая L задана параметрически
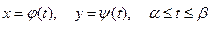 , то
, то
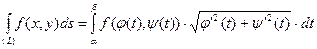 (**)
(**)
- Если кривая (L) в полярной системе координат задана уравнением
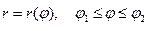 , а функция
, а функция 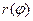 имеет непрерывную производную на отрезке
имеет непрерывную производную на отрезке 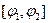 , то
, то
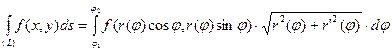 (***)
(***)
Пример 12. Вычислить криволинейный интеграл 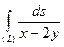 , где (L) - отрезок прямой
, где (L) - отрезок прямой 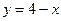 , соединяющий точки (3, 1) и (0, 4).
, соединяющий точки (3, 1) и (0, 4).
Решение.
Находим дифференциал длины дуги:
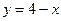 ,
, 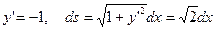 .
.
Используя формулу (*), получаем
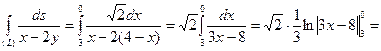
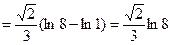 .
.
Ответ. 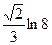 .
.
Пример 13. Вычислить криволинейный интеграл 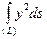 , где (L) – арка
, где (L) – арка
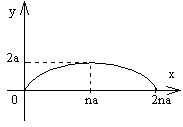 Рис. 16 Рис. 16 | циклоиды 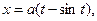 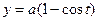 , , 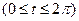 (рис.16). Решение. Находим (рис.16). Решение. Находим 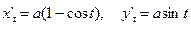 . Тогда . Тогда |
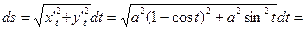
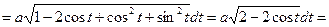
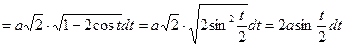 .
.
Используя формулу (**), получаем:
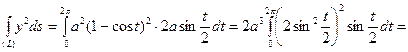
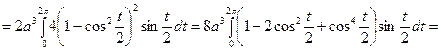
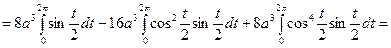
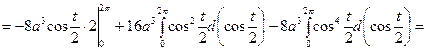
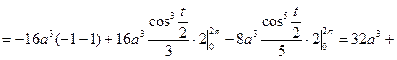
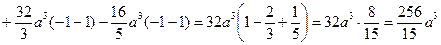 .
.
Ответ. 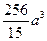 .
.
Пример 14. Вычислить 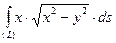 , где (L) – линия, заданная уравнением
, где (L) – линия, заданная уравнением 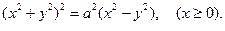
Решение.
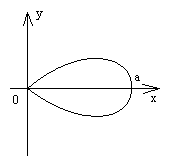 Рис. 17 Рис. 17 | Переходим к полярным координатам 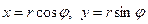 . Переведем подынтегральную функцию в полярные координаты: . Переведем подынтегральную функцию в полярные координаты: 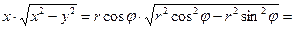 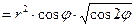 . Уравнение линии преобразуется к виду . Уравнение линии преобразуется к виду |
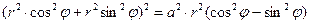 ,
,
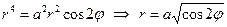 .
.
Неравенство 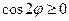 выполняется при
выполняется при 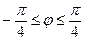 . Строим кривую
. Строим кривую 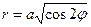 с учетом условия
с учетом условия 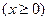 (рис. 17). Находим производную
(рис. 17). Находим производную 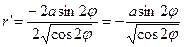 . Вычисляем криволинейный интеграл, используя формулу (***):
. Вычисляем криволинейный интеграл, используя формулу (***):

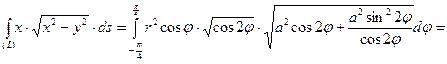
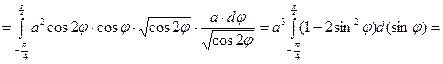
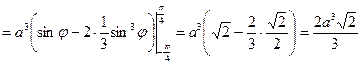 .
.
Ответ. 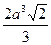 .
.
