Вычисление двойного интеграла
Случай прямоугольной области.
Пусть функция z = f(x,y) задана в прямоугольнике 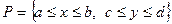 . Символ
. Символ 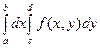 называется повторным интегралом в прямоугольнике (Р) и его смысл выражается равенством:
называется повторным интегралом в прямоугольнике (Р) и его смысл выражается равенством:
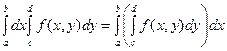 .
.
Теорема. Если в прямоугольнике 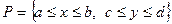 задана непрерывная функция z=f(x,y) и существует интеграл
задана непрерывная функция z=f(x,y) и существует интеграл 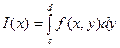 при
при 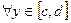 , то существует повторный интеграл
, то существует повторный интеграл 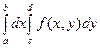 и справедливо равенство
и справедливо равенство
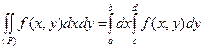 .
.
Теорема. Пусть функция z = f(x,y) непрерывна в замкнутой квадрируемой области (D), ограниченной снизу и сверху соответственно кривыми 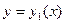 и
и 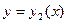 , а слева и справа прямыми x = a и x = b (a < b) и для
, а слева и справа прямыми x = a и x = b (a < b) и для 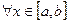 существует интеграл
существует интеграл 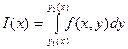 , тогда существует повторный интеграл
, тогда существует повторный интеграл 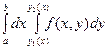 и справедливо равенство
и справедливо равенство
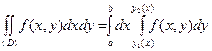 .
.
Аналогично 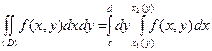 .
.
Так как для функции 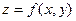 независимые переменные равноправны, то при вычислении двойного интеграла путем сведения его к повторному порядок интегрирования выбирают таким образом, чтобы вычисления оказались наиболее рациональными. В связи с этим иногда для упрощения вычислений изменяют порядок интегрирования.
независимые переменные равноправны, то при вычислении двойного интеграла путем сведения его к повторному порядок интегрирования выбирают таким образом, чтобы вычисления оказались наиболее рациональными. В связи с этим иногда для упрощения вычислений изменяют порядок интегрирования.
Пример 1. Записать двойной интеграл 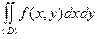 в виде повторных интегралов (двумя способами), если область (D) ограничена прямыми x = 1,
в виде повторных интегралов (двумя способами), если область (D) ограничена прямыми x = 1,
x = 2, y = 0, y = 4.
Решение.
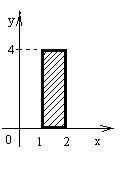 Рис. 2 Рис. 2 | Построив на чертеже прямые, ограничивающие область интегрирования, видим, что (D) представляет собой прямоугольник, стороны которого параллельны координатным осям (рис. 2). В этом случае обе переменные x и y изменяются в постоянных пределах 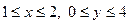 , а формулы для вычисления двойного интеграла принимают соответственно вид: , а формулы для вычисления двойного интеграла принимают соответственно вид: 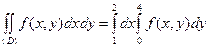 , , 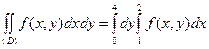 . . |
Пример 2. Записать двойной интеграл 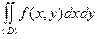 в виде повторных интегралов (двумя способами), если область (D) ограничена линиями x = 1,
в виде повторных интегралов (двумя способами), если область (D) ограничена линиями x = 1, 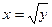 ,
,  .
.
Решение.
 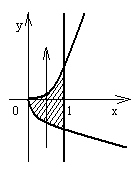 Рис. 3 Рис. 3 | Построим на чертеже линии, ограничивающие область интегрирования (рис.3): x = 1 – прямая, параллельная оси Oy; 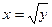 - одна ветвь параболы y=x2, расположенная справа от оси Oy; - одна ветвь параболы y=x2, расположенная справа от оси Oy;  - одна ветвь параболы - одна ветвь параболы 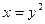 , расположенная ниже оси Ox. Видим, что (D) представляет собой криволинейную область. Возьмем сначала постоянные пределы по переменной x. Видим, что x изменяется в пределах от 0 до 1. Чтобы получить пределы интегрирования , расположенная ниже оси Ox. Видим, что (D) представляет собой криволинейную область. Возьмем сначала постоянные пределы по переменной x. Видим, что x изменяется в пределах от 0 до 1. Чтобы получить пределы интегрирования |
по переменной y, пересечем область (D) лучом, параллельным оси Oy и сонаправленным с ней. Граница области, которую луч пересекает при входе в область, будет нижней границей этой области, а ее уравнение, решенное относительно y, служит для установления нижнего предела интегрирования по y (y=y1(x)). В нашем случае  - нижний предел интегрирования по y. Граница области, которую луч пересекает, выходя из области, будет верхней границей этой области, а ее уравнение, решенное относительно y, служит для установления верхнего предела интегрирования по y (y=y2(x)). В нашем случае разрешая уравнение
- нижний предел интегрирования по y. Граница области, которую луч пересекает, выходя из области, будет верхней границей этой области, а ее уравнение, решенное относительно y, служит для установления верхнего предела интегрирования по y (y=y2(x)). В нашем случае разрешая уравнение 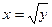 относительно y, получаем
относительно y, получаем 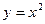 - верхний предел интегрирования по y. Таким образом, для каждого значения x из [0;1] переменная y принимает значения от
- верхний предел интегрирования по y. Таким образом, для каждого значения x из [0;1] переменная y принимает значения от 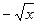 до
до 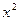 . Получим:
. Получим:
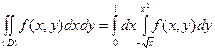 .
.
 Рис. 4 Рис. 4 | Если постоянные пределы взять по переменной y, то 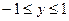 . Однако, проведя два луча, параллельных оси Ox (рис. 4), замечаем, что точки входа в область лежат на разных кривых: для луча, расположенного выше оси Ox эта точка лежит на ветви параболы . Однако, проведя два луча, параллельных оси Ox (рис. 4), замечаем, что точки входа в область лежат на разных кривых: для луча, расположенного выше оси Ox эта точка лежит на ветви параболы 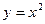 , а для луча, расположенного ниже оси Ox – на ветви параболы , а для луча, расположенного ниже оси Ox – на ветви параболы 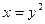 , точки же выхода лежат на одной прямой x=1. В связи с этим разобьем область (D) отрезком оси Ox на две области: (D1) для которой , точки же выхода лежат на одной прямой x=1. В связи с этим разобьем область (D) отрезком оси Ox на две области: (D1) для которой 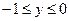 и (D2), для которой и (D2), для которой 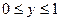 . . |
Далее, решив уравнения кривых относительно переменной x, получим пределы внутреннего интегрирования: нижний предел для (D1): 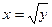 и нижний предел для (D2):
и нижний предел для (D2): 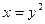 , верхний же предел для обеих областей будет x = 1. В итоге получим:
, верхний же предел для обеих областей будет x = 1. В итоге получим:
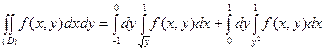 .то постоянные пределы взять по переменной нтегрирования по удет верхней границ
.то постоянные пределы взять по переменной нтегрирования по удет верхней границ
Пример 3. Изменить порядок интегрирования в интеграле
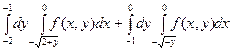 .
.
Решение.
Восстановим область интегрирования (D) (рис.5). Рассмотрим первый интеграл. Пределы интегрирования указывают уравнения кривых, дугами которых ограничена область интегрирования (D1): y = –2, y = –1, x = 0, 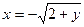 . Последнее уравнение преобразуется к виду
. Последнее уравнение преобразуется к виду 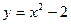 – квадратичная парабола, вершина которой сдвинута на 2 единицы вниз.
– квадратичная парабола, вершина которой сдвинута на 2 единицы вниз.
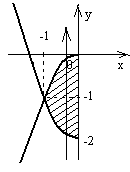 Рис. 5 Рис. 5 | Так как во внутреннем интеграле нижний предел содержится со знаком «минус», следует взять левую ветвь параболы. Рассмотрим второй интеграл. Область (D2) ограничена кривыми, уравнения которых: y = –1, y = 0, x = 0, 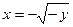 . Последнее уравнение преобразуется к виду . Последнее уравнение преобразуется к виду 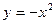 – квадратичная парабола, ветви которой направлены вниз. Так как во внутреннем интеграле нижний предел содержится со знаком «минус», следует взять левую ветвь параболы. Приступаем к изменению порядка интегрирования – квадратичная парабола, ветви которой направлены вниз. Так как во внутреннем интеграле нижний предел содержится со знаком «минус», следует взять левую ветвь параболы. Приступаем к изменению порядка интегрирования |
в данном интеграле, т.е. внутреннее интегрирование будем выполнять по переменной y, а внешнее – по переменной x. Для установления пределов интегрирования по переменной y проведем через область (D) луч параллельно оси Oy в направлении этой оси. Видим, что точка входа в область (D) лежит на параболе 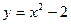 , а точка выхода – на параболе
, а точка выхода – на параболе 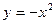 . Эти пределы являются нижним и верхним пределами интегрирования по переменной y. Так как для области (D)
. Эти пределы являются нижним и верхним пределами интегрирования по переменной y. Так как для области (D) 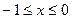 , то числа –1 и 0 будут пределами интегрирования по переменной x. В итоге получим:
, то числа –1 и 0 будут пределами интегрирования по переменной x. В итоге получим:
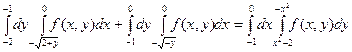 .
.
Пример 4. Изменить порядок интегрирования в интеграле
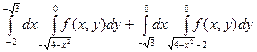 .
.
Решение.
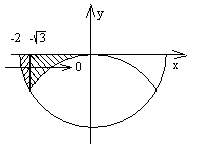 Рис. 6 Рис. 6 | Восстановим область интегрирования (D) (рис. 6). Рассмотрим первый интеграл. Пределы интегрирования указывают уравнения кривых, дугами которых ограничена область интегрирования (D1): 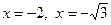 , , 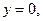 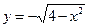 . Последнее уравнение преобразуется к виду . Последнее уравнение преобразуется к виду 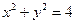 – окружность с центром в точке (0,0) и радиусом, равным 2. – окружность с центром в точке (0,0) и радиусом, равным 2. |
Так как во внутреннем интеграле нижний предел содержится со знаком «минус», следует взять нижнюю полуокружность.
Рассмотрим второй интеграл. Область (D2) ограничена кривыми, уравнения которых: 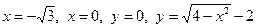 . Последнее уравнение преобразуется к виду
. Последнее уравнение преобразуется к виду 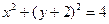 - окружность с центром в точке (0, -2) и радиусом, равным 2. Так как во внутреннем интеграле нижний предел содержится со знаком «плюс», следует взять верхнюю полуокружность.
- окружность с центром в точке (0, -2) и радиусом, равным 2. Так как во внутреннем интеграле нижний предел содержится со знаком «плюс», следует взять верхнюю полуокружность.
Приступаем к изменению порядка интегрирования в данном интеграле, т.е. внутреннее интегрирование будем выполнять по переменной x, а внешнее – по переменной y. Для установления пределов интегрирования по переменной x проведем через область (D) луч параллельно оси Ox в направлении этой оси. Видим, что точка входа в область (D) лежит на окружности 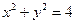 , а точка выхода – на окружности
, а точка выхода – на окружности 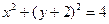 . Выражаем из этих уравнений переменную x:
. Выражаем из этих уравнений переменную x: 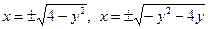 . Из рис. 6 видно, что область (D) ограничивают левые полуокружности, следовательно берем значение x со знаком «минус». Получаем
. Из рис. 6 видно, что область (D) ограничивают левые полуокружности, следовательно берем значение x со знаком «минус». Получаем 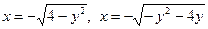 - нижний и верхний пределы интегрирования по переменной x. Так как для области (D)
- нижний и верхний пределы интегрирования по переменной x. Так как для области (D) 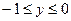 , то числа -1 и 0 будут пределами интегрирования по переменной y. В итоге получим:
, то числа -1 и 0 будут пределами интегрирования по переменной y. В итоге получим:
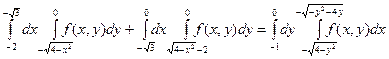 .
.
Пример 5. Вычислить двойной интеграл 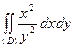 , где область (D) ограничена линиями
, где область (D) ограничена линиями 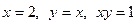 .
.
Решение.
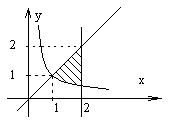 Рис. 7 Рис. 7 | Область интегрирования (D) ограничена прямыми 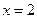 , , 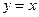 и гиперболой и гиперболой 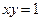 (рис. 7). Выберем постоянные пределы интегрирования по переменной x: от 1 до 2. При этом y изменяется от (рис. 7). Выберем постоянные пределы интегрирования по переменной x: от 1 до 2. При этом y изменяется от 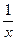 до до 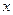 . Тогда . Тогда |
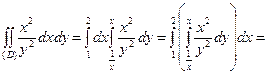
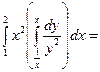
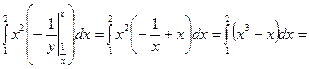
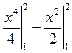
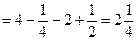 .
.
Ответ. 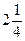 .
.
Замечание. Если взять постоянные пределы по переменной y, то данный двойной интеграл будет представлен в виде суммы двух повторных интегралов, в связи с чем его вычисление усложняется.
