Второе начало термостатики
В качестве постулата второго начала термостатики используется утверждение, что «температура есть единственная функция состояния, определяющая направление самопроизвольного теплообмена».
Для вывода математического выражения второго начала термостатики рассмотрим адиабатно изолированную систему, состоящую из термически сопряженных тел. Первое тело (I) - любое тело (например,
реальный газ), совершает произвольные процессы - обратимые и необратимые, второе тело (II) - контрольное тело - идеальный газ, совершает обратимый круговой процесс. Оба тела в каждый момент имеют одинаковую
температуру (tI = tII = t).
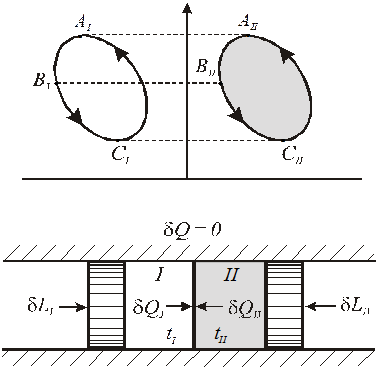 |
Первое и второе тело осуществляют разнообразные процессы изменения состояния, к ним извне подводится (или отводится) работа, между телами происходит теплообмен, но для адиабатно изолированной системы выполняется обязательное условие
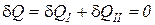 . (1)
. (1)
Разделим уравнение (1) на некоторую функцию, зависящую только от температуры t(t). Для идеального газа эта функция равна абсолютной температуре t(tII) = TII . С учетом равенства температур двух тел получаем
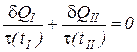 . (2)
. (2)
Так как тела I и II возвращаются в исходное состояние одновременно (согласно теореме теплового равновесия тел в равновесных круговых процессах) последнее уравнение можно интегрировать по замкнутому контуру
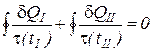 . (3)
. (3)
Второй интеграл по замкнутому контуру для идеального газа, как интеграл функции состояния, равен нулю
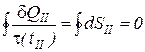 . (4)
. (4)
Поэтому и первый круговой интеграл в уравнении (3) также равен нулю
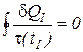 . (5)
. (5)
Если круговой интеграл равен нулю, то это значит, что подынтегральное выражение представляет из себя полный дифференциал некоторой функции состояния, названной энтропией ( 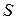 ), а функция t(tI) является интегрирующим делителем
), а функция t(tI) является интегрирующим делителем
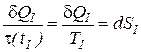 . (6)
. (6)
Так как тело I - любое тело и свойства тел I и II независимы, полученное выражение (6) распространяется на все равновесные процессы изменения состояния любых систем. Выбранная функция t(t), которая не зависит от вида тел, называется абсолютной температурой t(t)= Т, а температурная шкала называется абсолютной термодинамической.
Таким образом, получаем математическое выражение второго начала термостатики - принципа существования энтропии и абсолютной температуры для любых равновесных систем
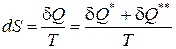 (7)
(7)
Второе начало термостатики утверждает принцип существования энтропии и абсолютной температуры как функции состояния любой равновесной термодинамической системы, совершающей обратимые или необратимые процессы.
Вопрос 19.
Следствия второго начала термостатики широко применяются в термодинамических расчетах и формулируются на основе анализа его математического выражения (162), (163).
Следствие I. Совместное выражение первого начала термодинамики и второго начала термостатики позволяет получить дифференциальное уравнение термодинамики, которое связывает между собой все термодинамические свойства веществ
T ds= cv dT + 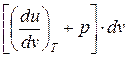 = cp dT +
= cp dT + 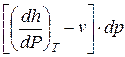 .
.
Следствие II. Координаты Т - S являются универсальными координатами термодинамического теплообмена.
Следствие III. Адиабатный процесс является процессом изоэнтропийным.
Так как в адиабатном процессе теплообмен отсутствует (dQ = 0), то, согласно второму началу термостатики (162), в таком процессе изменение энтропии dS = 0 (S = idem). Согласно этому следствию, показатель адиабатного процесса ( 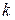 ) равен показателю изоэнтропийного процесса (
) равен показателю изоэнтропийного процесса ( 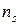 )
)
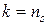 .
.
Следствие IV. Коэффициент полезного действия и холодильный коэффициент термодинамических циклов тепловых машин не зависят от вида цикла и природы рабочего тела, а определяются лишь средними абсолютными температурами рабочего тела в процессах подвода и отвода теплоты.
(8)
Следствие V. Коэффициент полезного действия и холодильный коэффициент цикла Карно всегда выше этих коэффициентов эффективности для любых других термодинамических циклов тепловых машин, осуществляемых в одинаковом диапазоне предельных температур рабочего тела ( 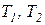 ).
).
Это следствие вытекает из анализа соотношений по определению КПД цикла Карно 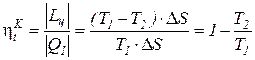 и любого термодинамического цикла
и любого термодинамического цикла 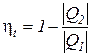 =
= 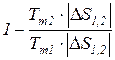 =1 -
=1 - 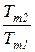 теплового двигателя. Вследствие того, что Т1 >Тm1 и Т2 < Тm2
теплового двигателя. Вследствие того, что Т1 >Тm1 и Т2 < Тm2
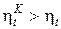 . (9)
. (9)
Аналогичный вывод можно сделать и при сравнении холодильных коэффициентов обратных циклов
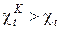 . (10)
. (10)
Рассматриваемое следствие утверждает, что цикл Карно является эталонным циклом, по сравнению с которым можно определить термодинамическое совершенство любого цикла, осуществляемого в заданном интервале предельных значений температур рабочего тела.
Следствие VI. Изменение энтропии системы равно сумме изменений энтропии всех тел, входящих в систему (теорема аддитивности энтропии).
Количество теплоты, полученное в элементарном процессе системой, состоящей из 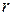 тел, можно определить из соотношения
тел, можно определить из соотношения
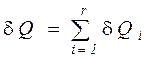 , (11)
, (11)
что и подтверждает справедливость сформулированного следствия
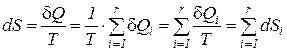 . (12)
. (12)
Вопрос №20.
В рамках классической термодинамики второе начало термодинамики формулируется, как обобщённый принцип существования и возрастания энтропии, то есть 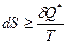 . Если
. Если 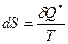 , то процесс – обратимый. Если
, то процесс – обратимый. Если 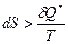 , то процесс реальный.
, то процесс реальный.
Для изолированной системы (то есть 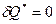 ) выполняется принцип существования энтропии:
) выполняется принцип существования энтропии: 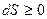 . Для реальной системы выполняется принцип возрастания энтропии:
. Для реальной системы выполняется принцип возрастания энтропии: 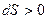 .
.
Поскольку в рамках классической формулировки второго начала термодинамики невозможно определение энтропии реального газа, то этот процесс делят на два этапа:
1. Второе начало термодинамики (принцип существования энтропии) 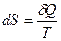 .
.
2. Второе начало термодинамики (принцип возрастания энтропии) 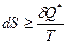 .
.
Математическое выражение принципа существования энтропии: 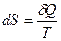 . При этом выполняются следующие условия:
. При этом выполняются следующие условия:
1. Абсолютная температура является единственной функцией (спросить!!!).
2. Невозможен одновременный теплообмен.
3. Невозможно в рамках одной пространственной системы осуществить одновременное превращение работы в тепло и тепла в работу.
Вопрос № 21
Следствие I. Невозможно осуществление полного превращения теплоты работу, т.е. нельзя создать вечный двигатель второго рода с коэффициентом полезного действия равным единице.Это следствие вытекает из постулата в формулировке Томсона-Кельвина, согласно которой всякий тепловой двигатель должен иметь как минимум два источника теплоты с различной температурой Т1 и Т2. Следовательно, всегда ú 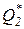 ç> 0 и поэтому
ç> 0 и поэтому
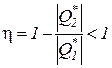 .
.
Следствие II. КПД реального теплового двигателя и холодильный коэффициент реальной холодильной машины, в которых осуществляются циклы при температурах внешних источников Т1 и Т2 , всегда меньше КПД и холодильного коэффициента обратимых тепловых машин, циклы в которых осуществляются между теми же внешними источниками:
h < hобр ; c < cобр .
Следствия принципа существования энтропии.
1. 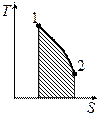 Изменение энтропии всей системы может быть подсчитано отдельно:
Изменение энтропии всей системы может быть подсчитано отдельно: 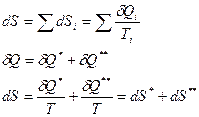
2. Площадь под графиком 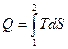 . Если
. Если 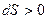 , то
, то 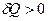 , если
, если 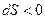 , то
, то 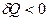 .
.
3. 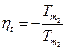
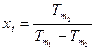
4. Математическое определение абсолютной температуры: 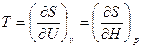 .
.
Принцип возрастания энтропии.
Работа может быть полностью превращена в теплоту: 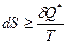 .
.
Принцип необратимости процессов в природе:
1. 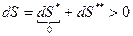 .
.
2. 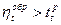 .
.
3. Абсолютная температура 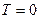 недостижима, так как
недостижима, так как 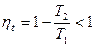 . Так как
. Так как 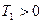 , то
, то 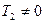 .
.
Вопрос №22
Смеси жидкостей, паров и газов.
Термодинамическая смесь – система, состоящая из 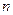 химически невзаимодействующих друг с другом компонентов.
химически невзаимодействующих друг с другом компонентов.
Состав смеси задаётся либо массовой концентрацией компонентов - 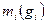 , либо молярным составом -
, либо молярным составом - 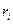 (объёмный).
(объёмный).
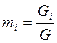 , где
, где 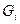 - масса одного компонента смеси,
- масса одного компонента смеси, 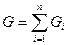 - масса всей смеси.
- масса всей смеси.
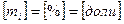
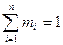
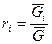 , где
, где 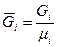 - число киломолей вещества,
- число киломолей вещества, 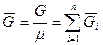 - число киломолей смеси.
- число киломолей смеси.
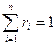
Для смеси нужно уметь определять среднюю молекулярную массу 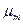 и среднюю газовую постоянную
и среднюю газовую постоянную 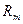 .
.
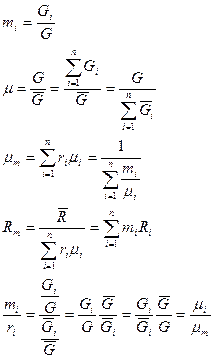
Если смесь является идеальным газом, то 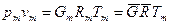 .
.
Если смесь является реальным газом, то 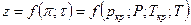 .
.
Псевдокритические параметры:
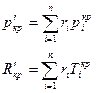
Схемы смешивания газов.
1. 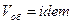 , следовательно
, следовательно 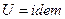 .
.
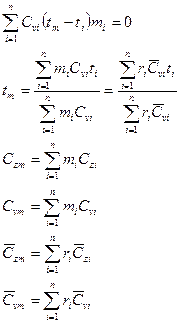
2. 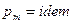 , следовательно
, следовательно 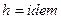 .
.
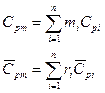
Закон Дальтона: давление смеси равно сумме парциальных давлений компонентов.
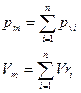
Парциальное давление.
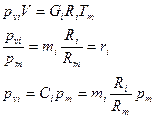
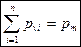
Вопрос № 23
Истечение паров, жидкостей и газов.
Процесс истечения – процесс переноса вещества из области с одним давлением в область с другим.
Действительный процесс истечения характеризуется необратимыми потерями и неравномерностью распределения скоростей в потоке. В теории истечение рассматривается, как обратимый процесс, а переход к реальным характеристикам осуществляется с помощью двух коэффициентов: коэффициента скорости - 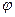 и коэффициента расхода -
и коэффициента расхода - 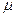 , причём эти коэффициенты определяются экспериментальным путём. Оба коэффициента показывают различия между теоретическими и действительными величинами.
, причём эти коэффициенты определяются экспериментальным путём. Оба коэффициента показывают различия между теоретическими и действительными величинами.
Нас интересуют следующие величины:
1. Линейная скорость - 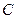 ,
, 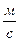 .
.
2. Массовая скорость - 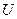 ,
, 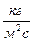 .
.
3. Массовый расход - 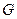 ,
, 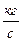 .
.
Задача решается на базе следующих уравнений:
1. Первое начало термодинамики: 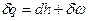 .
.
2. Уравнение процесса:
a. Политропный процесс: 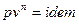 .
.
b. Адиабатный процесс: 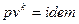 .
.
3. Уравнение неразрывности в интегральном виде: 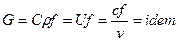 .
.
4. Уравнение состояние.
Основные соотношения процесса истечения.
Уравнение распределения потенциальной работы:
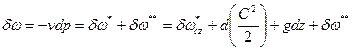 .
.
Так как рассматриваются обратимые потери, то 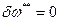 .
.
Так как рассматривается чистое движение, то 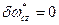 .
.
Следовательно: 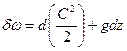 .
.
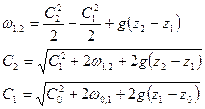
Так как рассматриваются короткие каналы, то 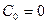 ,
, 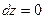 .
.
Выражение для линейной скорости: 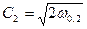 .
.
Выражение для массовой скорости: 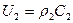 .
.
Выражение для массового расхода: 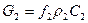 .
.
Основные исходные соотношения.
Уравнение для линейной скорости: 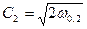 .
.
Уравнение для массовой скорости: 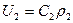 .
.
Уравнение для массового расхода: 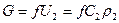 .
.
Истечение несжимаемой (капельной) жидкости.
Условия не сжимаемости жидкости: 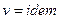 ,
, 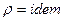 .
.
Рассматриваем изохорный процесс. Потенциальную работу можно найти по следующей формуле: 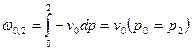 .
.
Подставив это в уравнение для линейной скорости, получим: 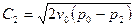 .
.
Графическое представление зависимости скорости то перепада давления:

Подставив это в уравнение для массовой скорости, получим: 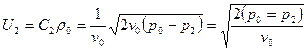 .
.
Подставив это в уравнение для массового расхода, получим: 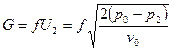 .
.
Действительная линейная скорость отличается от теоретической, поэтому вводят коэффициент скорости 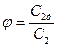 , где
, где 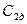 - действительная линейная скорость,
- действительная линейная скорость, 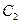 - теоретическая линейная скорость. Поэтому действительную линейную скорость можно найти по формуле:
- теоретическая линейная скорость. Поэтому действительную линейную скорость можно найти по формуле: 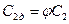 .
.
 При течении жидкости в трубе с переменным сечением наблюдается отрыв струи от стенок и площадь сечения течения становится меньше площади сечения трубопровода. В связи с этим вводят коэффициент сжатия струи
При течении жидкости в трубе с переменным сечением наблюдается отрыв струи от стенок и площадь сечения течения становится меньше площади сечения трубопровода. В связи с этим вводят коэффициент сжатия струи 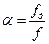 , при этом он лежит в пределах от 0.6 до 1. Если профиль канала параболический, то
, при этом он лежит в пределах от 0.6 до 1. Если профиль канала параболический, то 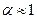 .
.
Действительный массовый расход можно найти по формуле: 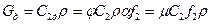 , где
, где 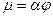 - коэффициент расхода.
- коэффициент расхода.
Вопрос № 24.
Истечение сжимаемых жидкостей (паров и газов).
Условия сжимаемости жидкости: 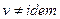 ,
, 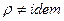 .
.
Рассматриваем политропный процесс истечения: 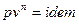 . В случае, если
. В случае, если 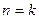 , то получаем адиабатный процесс истечения.
, то получаем адиабатный процесс истечения.
Потенциальную работу можно найти по следующей формуле: 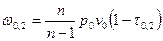 , где
, где 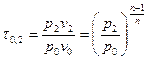 . Тогда
. Тогда 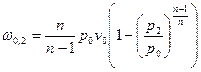 . Подставив полученное выражение в уравнение для линейной скорости, получим:
. Подставив полученное выражение в уравнение для линейной скорости, получим: 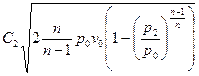 - уравнение линейной скорости для политропного процесса.
- уравнение линейной скорости для политропного процесса.
Уравнение линейной скорости для адиабатного процесса 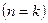 будет иметь следующий вид:
будет иметь следующий вид: 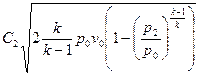 .
.
В уравнение для массовой скорости 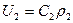 входит плотность
входит плотность 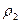 , которая меняется в течение процесса. Из уравнения политропного процесса
, которая меняется в течение процесса. Из уравнения политропного процесса 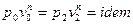 можно получить уравнение для плотности:
можно получить уравнение для плотности: 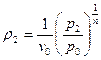 . Подставив полученное выражение уравнение для массовой скорости, получим:
. Подставив полученное выражение уравнение для массовой скорости, получим: 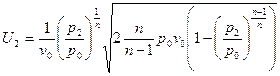 или
или 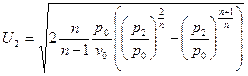 - уравнение массовой скорости для политропного процесса.
- уравнение массовой скорости для политропного процесса.
Уравнение массовой скорости для адиабатного процесса 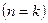 будет иметь следующий вид:
будет иметь следующий вид: 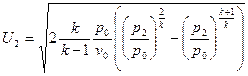 .
.
Обычно отношение 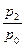 обозначают за
обозначают за 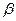 . Коэффициент
. Коэффициент 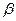 лежит в пределах от 0
лежит в пределах от 0 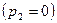 до 1
до 1 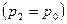 .
.
Графическое представление зависимости линейной и массовой скоростей от отношения давлений.
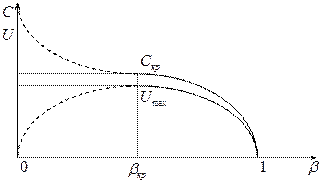 В зависимости от соотношений давлений возможны три режима:
В зависимости от соотношений давлений возможны три режима:
1. До критический (дозвуковой) режим - 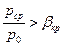 .
.
2. Критический (звуковой) режим - 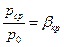 .
.
3. За критический (сверхзвуковой) режим - 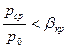 .
.
Для определения режима нужно знать значение 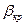 . Для этого нужно найти экстремумы функции
. Для этого нужно найти экстремумы функции 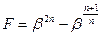 . То есть
. То есть 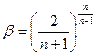 , при
, при 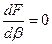 .
.
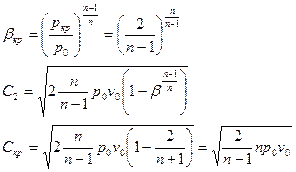
Характеристика растяжения сжатия: 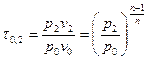
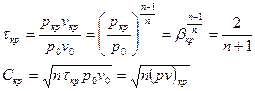
Для адиабатного процесса: 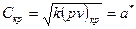 , где
, где 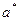 - скорость звука.
- скорость звука.
Для идеального газа: 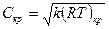 .
.
Чтобы массовая скорость стала критической, то есть 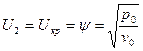 .
.
Массовый расход: 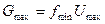 .
.
Вопрос №25.
Переход через критическую скорость (сопло Лаваля).

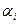 - угол раскрытия канала.
- угол раскрытия канала.
Начальные параметры: 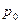 ,
, 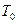 ,
, 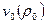 .
.
Параметры среды: 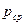 ,
, 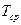 ,
, 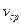 .
.
Можно поставить две задачи:
1. Найти линейную скорость, массовую скорость и массовый расход, при известной геометрии аппарата.
2. Найти геометрию аппарата, при известном массовом расходе.
Решаем вторую задачу.
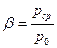
Сравнивая величину 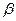 с
с 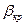 , получим три варианта:
, получим три варианта:
1. Докритический режим, 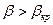 .
.
2. Критический режим: 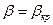 .
.
3. Закритический режим: 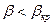 .
.
Нужно найти площади сечений: 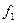 ,
, 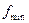 ,
, 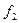 .
.
Уравнение неразрывности: 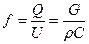 . Подставляя в это уравнение массовые скорости, можно найти площади сечений, но для каждого случая нужно знать величину
. Подставляя в это уравнение массовые скорости, можно найти площади сечений, но для каждого случая нужно знать величину 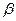 , то есть нужно с помощью уравнений процессов (
, то есть нужно с помощью уравнений процессов ( 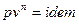 и
и 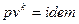 ) найти давления
) найти давления 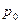 ,
, 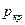 ,
, 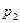 . Зная площади сечений можно найти характеристические размеры сечений.
. Зная площади сечений можно найти характеристические размеры сечений.
Длины можно найти геометрически: 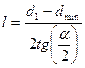 , где
, где 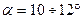 .
.
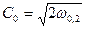
Для адиабатного процесса 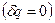 потенциальная работа находится по формуле:
потенциальная работа находится по формуле: 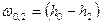 , тогда линейная скорость
, тогда линейная скорость 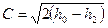 .
.

Вопрос № 26
Особенности истечения из каналов переменного сечения.
Уравнение истечения: 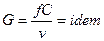 .
.
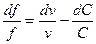 (а)
(а)
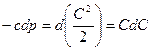
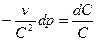 (б)
(б)
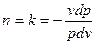
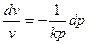 (в)
(в)
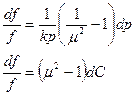
Если 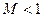 (докритический режим), то при сужающемся канале
(докритический режим), то при сужающемся канале 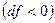 давление будет падать
давление будет падать 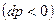 , а скорость возрастать
, а скорость возрастать 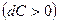 . Такой аппарат называется соплом. При расширяющемся канале
. Такой аппарат называется соплом. При расширяющемся канале 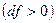 давлении будет расти
давлении будет расти 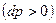 , а скорость падать
, а скорость падать 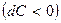 . Такой аппарат называется диффузор.
. Такой аппарат называется диффузор.
Если 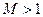 (закритический режим), то при сужающемся канале
(закритический режим), то при сужающемся канале 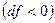 давление будет расти
давление будет расти 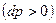 , а скорость падать
, а скорость падать 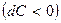 . Такой аппарат называется диффузор. При расширяющемся канале
. Такой аппарат называется диффузор. При расширяющемся канале 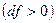 давление будет падать
давление будет падать 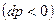 , а скорость возрастать
, а скорость возрастать 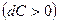 . Такой аппарат называется соплом.
. Такой аппарат называется соплом.
Вопрос №27.
Дросселирование.
Дросселирование – процесс движения паров, жидкостей и газов через внезапное сужение(местное сопротивление).
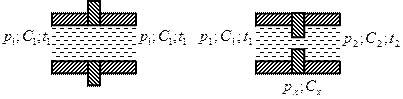
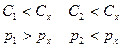
Для быстро протекающего процесса можно теплотой внешнего теплообмена пренебречь, то есть 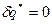 , также
, также 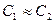 ,
, 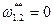 .
.
Первое начало термодинамики: 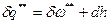 , следовательно,
, следовательно, 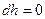 , или
, или 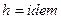 , то есть процесс изоэнтальпийный, но он реальный, то есть протекает с необратимыми потерями давления.
, то есть процесс изоэнтальпийный, но он реальный, то есть протекает с необратимыми потерями давления.
Явление изменения температуры газа или жидкости при адиабатном дросселировании называется эффектом Джоуля – Томсона 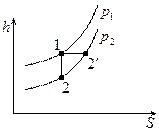 .
.
Для характеристики дроссельного процесса вводится коэффициент Джоуля-Томпсона: 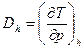 , который можно найти по следующей формуле
, который можно найти по следующей формуле 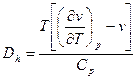 . Если
. Если 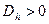 , то
, то 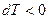 . Если
. Если 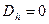 , то
, то 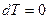 . Если
. Если 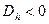 , то
, то 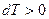 .
.
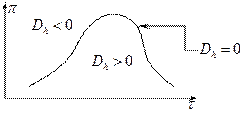
Дросселирование является изоэнтальпийным процессом, при котором 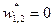 .
.
Для идеального газа 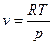 , тогда
, тогда 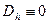 , следовательно
, следовательно 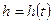 .
.
Вопрос №28
Процесс парообразования. Определение параметров влажного или насыщенного пара.
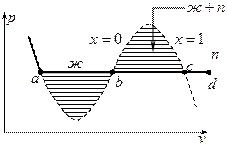 Возьмём один килограмм жидкости при температуре равной нулю и каком-то давлении
Возьмём один килограмм жидкости при температуре равной нулю и каком-то давлении 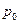 .
.
При нагреве растут, и температура, и объём – точка 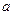 . В точке
. В точке 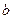 начинается кипение. Давление -
начинается кипение. Давление - 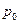 , температура равняется температуре насыщения -
, температура равняется температуре насыщения - 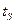 . В точке
. В точке 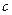 - появляется сухой насыщенный пар, давление -
- появляется сухой насыщенный пар, давление - 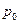 , температура
, температура 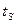 . В точке
. В точке 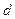 образуется перегретый пар, давление -
образуется перегретый пар, давление - 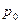 , температура равняется температуре перегретого пара
, температура равняется температуре перегретого пара 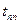 .
.
Степень сухости: 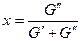 , где
, где 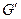 - масса кипящей жидкости,
- масса кипящей жидкости, 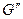 - масса сухого пара.
- масса сухого пара.
Влажность: 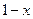 .
.
Насыщенный пар.
Давление насыщения: 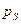 .
.
Температура насыщения: 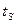 .
.
Теплота фазового перехода: 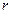 , при этом теплота фазового перехода зависит от давления, то есть
, при этом теплота фазового перехода зависит от давления, то есть 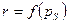 - уравнение фазовых переходов.
- уравнение фазовых переходов.
Определение параметров насыщенного пара.
Дано давления - 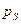 и степень сухости
и степень сухости 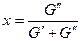 .
.
Любую характеристику можно определить, как 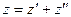 .
.
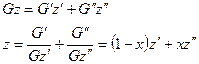
Например:
Удельный объём: 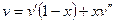 .
.
Энтальпия: 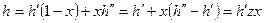 .
.
Энтропия: 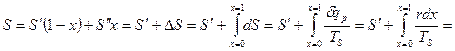
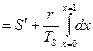 .
.
Для полного испарения: 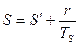 .
.
Диаграмма 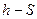 для водяного пара:
для водяного пара:
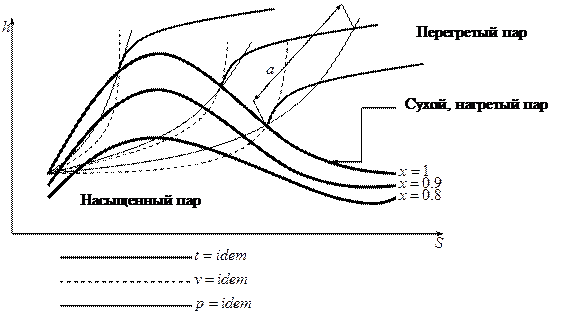
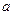 - степень перегрева.
- степень перегрева.
С помощью графика можно найти 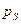 ,
, 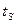 ,
, 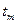 ,
, 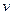 ,
, 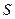 , и
, и 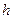 . С помощью этих данных можно вычислить энергию по формуле:
. С помощью этих данных можно вычислить энергию по формуле: 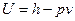 .
.
Вопрос № 29
