Обеспечение устойчивости и повышение запаса устойчивости
Способы придания системам автоматического регулирования устойчивости и достаточного запаса устойчивости (способы стабилизации и демпфирования) разнообразны.
В § 5.1 рассматривалась возможность решения этой задачи выбором основных элементов регулятора и изменением их динамических свойств с помощью местных обратных связей. Выясним, как влияет на устойчивость изменение наиболее характерного параметра - постоянной времени апериодического звена. На рис. 5.6 сплошными линиями изображены логарифмические частотные характеристики разомкнутой системы с передаточной функцией (5.14) . При увеличении T 1 с 0,5 до 1 с характеристики принимают положение, показанное пунктирными линиями. Увеличение постоянной времени Т, приводит к увеличению запаса устойчивости по фазе с g 0 до g 1 =60 0 . Заметим, что сопрягающая частота w 1 =1/T 1 расположена левее частоты среза w c .

Если же сопрягающая частота апериодического звена расположена правее частоты среза, то увеличение постоянной времени этого звена уменьшит запас устойчивости. Очевидно, что изменение постоянной времени колебательного звена влияет на запас устойчивости аналогичным образом. Влияние постоянной времени форсирующего звена (передаточная функция W ф =k (Ts+1) ) противоположно.
Итак, если сопрягающая частота апериодического или колебательного звена расположена левее частоты среза логарифмической амплитудно-частотной характеристики разомкнутой системы, а сопрягающая частота форсирующего звена расположена правее частоты среза, то увеличение постоянной времени каждого из этих звеньев ведет к увеличению запаса устойчивости [4]. Указанная зависимость справедлива лишь при условии, что сопрягающая частота расположена на некотором удалении (около одной декады) от частоты среза.
Встречаются, однако, структуры, для которых указанное правило не выполняется. Пусть, например, передаточная функция разомкнутой системы
W=k (T 0 s+1) /[ (T 1 s+1) (T 2 s+1) (T 3 s+1) ],
где k=100; T 0 =0.1c; T 1 =1c; T 2 =0,5c; T 3 =0,01c.
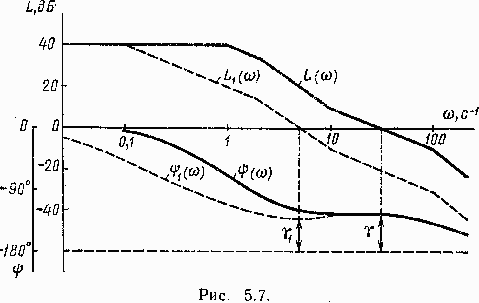
Логарифмические частотные характеристики этой системы показаны на рис. 5.7 сплошными линиями. При изменении T 1 с 1с на 10с характеристики принимают положение, показанное на рис. 5.7 пунктиром. Запас устойчивости по фазе с g =61 0 уменьшился до g 1 =47 0 .
Другой и наиболее применяемый путь стабилизации и демпфирования системы - введение в ее прямую цепь дополнительных звеньев. С этой целью используют сложные динамические звенья.
В зависимости от структуры и параметров системы введение одного и того же звена может дать различные результаты. Так, в § 5.2 уже было показано, что введение интегрирующего звена может вести и к уменьшению, и к увеличению запаса устойчивости. Поэтому правильный выбор дополнительного звена можно сделать только зная структуру и параметры системы.
Рассмотрим наиболее характерные случаи стабилизации и демпфирования систем путем введения дополнительных звеньев. Предположим, что разомкнутая система описывается передаточной функцией (5.14) при k=100; T 1 =0,05c; T 2 =0,01c и T 3 =0,001c. В разомкнутом состоянии система устойчива и ее логарифмические частотные характеристики, изображенные на рис. 5.8 сплошными линиями, свидетельствуют о неустойчивости замкнутой системы, так как фаза достигает -180° при частоте, меньшей частоты среза.
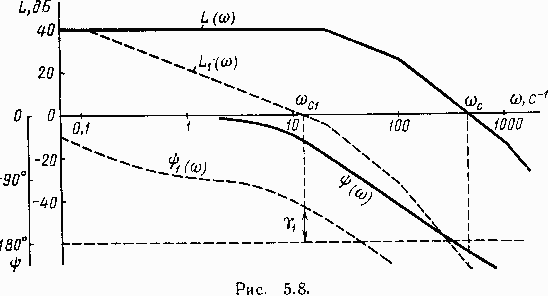
Введем в прямую цепь системы дополнительное звено с передаточной функцией W Д =1/ (T Д s+1) , где T Д =8c . Тогда характеристики системы принимают положение, показанное на рис. 5.8 пунктирными линиями, и на основании их можно видеть, что замкнутая система становится устойчивой. Запас по фазе составляет g =51 0 . Увеличением постоянной времени Т Д дополнительного звена запас устойчивости по фазе можно увеличить.
Устойчивость достигнута введением апериодического звена, постоянная времени которого значительно больше постоянных времени имеющихся апериодических звеньев. При этом высокочастотная часть логарифмической амплитудно-частотной характеристики сместилась вниз. Также изменилась и логарифмическая фазочастотная характеристика. Такой прием обеспечения устойчивости или повышения запаса устойчивости называют демпфированием с подавлением высоких частот (демпфированием с внесением отрицательных фазовых сдвигов) .
Апериодическое звено с большой постоянной времени представляет собой фильтр низких частот и подавляет высокочастотные помехи. В этом достоинство данного вида демпфирования. Значительное уменьшение частоты среза и, следовательно, быстродействия системы является весьма существенным недостатком.
Если ось абсцисс пересекается ЛАЧХ, имеющей наклон -20дБ/дек и слева от частоты среза только одна сопрягающая частота, то система остается устойчивой и запас устойчивости не изменяется при увеличении передаточного коэффициента k разомкнутой системы. Нужно только одновременно с увеличением k пропорционально увеличивать постоянную времени апериодического звена.
Введением форсирующего звена могут быть обеспечены устойчивость и необходимый запас устойчивости при любой передаточной функции исходной системы (если она становится структурно устойчивой) . Одновременно увеличивается и быстродействие. Однако существенно увеличивается и влияние высокочастотных помех. Последнее обстоятельство является серьезным недостатком данного вида демпфирования и ограничивает его применение.
