Одноиндексная модель У. Шарпа

Модель Г. Марковица требует определения математического ожидания и дисперсии доходности каждой ценной бумаги, а также ковариации между доходами отдельных ценных бумаг. Последняя операция является особенно трудоемкой. Так, например, для анализа 100 акций необходимо рассчитать около 500 ковариаций.

У. Шарпу удалось упростить модель Г. Марковица, предложив, так называемую, индексную модель. Мы рассмотрим простой вариант – одноиндексную модель У. Шарпа.

В основе одноиндексной модели лежит линейная регрессионная модель, которая связывает доходность какой-либо ценной бумаги с тем или иным рыночным параметром (валовым внутренним продуктом, уровнем инфляции, индексом потребительских цен и т.п.). Шарп У. связывал доходность одной ценной бумаги рыночного портфеля с доходностью всего портфеля, в качестве которого принимал пакет акций, входящих в биржевой индекс S&P500.^[16]

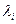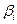Уравнение линейной регрессии строится следующим образом. На основании исторических данных определяются параметры и уравнения:

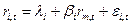, где

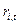- доходность 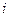-й ценной бумаги в момент ;

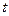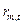- доходность рыночного портфеля в момент ;

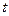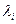- свободный член уравнения, так называемый коэффициент «альфа»;

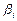- коэффициент «бета»

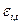- случайная ошибка (предполагается, что математическое ожидание случайной ошибки равно 0).

Неизвестные параметры 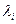и 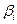регрессионной модели 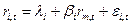определяются методом наименьших квадратов из условия минимизации суммы квадратов случайной ошибки:

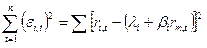
Необходимо взять производные данного выражения по 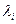и 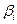, и приравнять их нулю.

Минимум случайной ошибки достигается при следующих соотношениях:

;

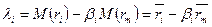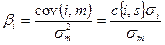
Заметим, что минимум суммы квадратов отклонений достигается тогда, когда отклонения считаются от математического ожидания случайной величины, то есть когда теоретические значения доходности ценной бумаги равные математическому ожиданию доходности.

При минимальной случайной ошибке коэффициент «альфа» равен разнице между среднеарифметической доходностью 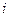-й ценной бумаги и среднеарифметической доходностью портфеля, умноженной на коэффициент «бета», а коэффициент «бета» - отношению ковариации 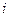-й ценной бумаги с рыночным портфелем к дисперсии портфеля. Напомним, что дисперсия равна ковариации ценной бумаги с самой собой.

Напомним также, что коэффициенты ковариации и корреляции связаны следующими соотношениями:

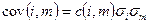
Теперь проведем расчеты необходимых показателей случайных величин (математического ожидания и дисперсии), по имеющимся историческим данным за 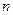- моментов времени.

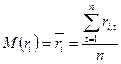
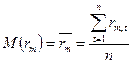
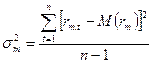
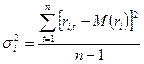
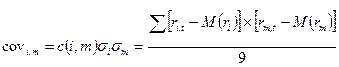
На основе вычисленных показателей случайных величин мы уже можем рассчитать параметры 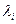и 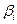регрессионного уравнения. Напомним, что:

;

.

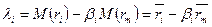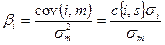Для решения задачи оптимизации портфеля ценных бумаг, подобные расчеты мы должны провести для каждой ценной бумаги из портфеля.

Итак, мы рассчитали параметры регрессионного уравнения, которые дают минимальную величину случайной ошибки. Но нам неизвестна еще эта величина.

Уточним допущения предложенной регрессионной модели:

1. Математическое ожидание ожидаемой случайной ошибки для всех акций равно 0;

2. Дисперсия случайных ошибок для всех акций - постоянная величина;

3. Для каждой акции портфеля отсутствует корреляция между наблюдаемыми на каждом шаге расчета случайными ошибками, то есть ;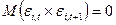

4. Отсутствует корреляция между случайными ошибками любых двух ценных бумаг в портфеле, то есть ;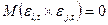

5. Отсутствует корреляция между случайными ошибками регрессионного уравнения и рыночной доходности, то есть .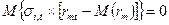

Теперь мы можем корректно рассчитать дисперсию случайной ошибки для каждой ценной бумаги.

По определению дисперсии, 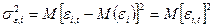. Так как 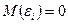по первому допущению.

Поэтому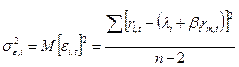

Среднеарифметическое значение дисперсии случайной ошибки вычисляется делением на 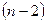, так как две степени свободы были потеряны при вычислени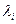и и .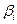

Теперь мы можем вычислить среднеарифметическое значение доходности и риск (дисперсию) любой отдельной ценной бумаги портфеля с учетом случайной ошибки. Вернемся к нашей основной регрессионной модели:

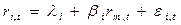, где

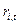- доходность 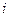-й ценной бумаги в момент ;

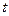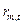- доходность рыночного портфеля в момент ;

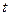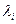- свободный член уравнения, так называемый коэффициент «альфа»;

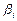- коэффициент «бета»

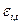- случайная ошибка (предполагается, что математическое ожидание случайной ошибки равно 0).

.

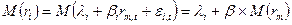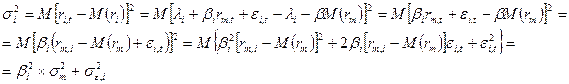
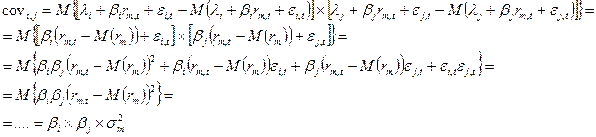
Итак, подведем итоги:

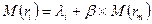
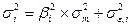
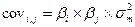
Становится понятным, почему одноиндексная модель оптимизации портфеля ценных бумаг требует меньше расчетов, чем модель Марковица Г. Дело в том, что отпадает необходимость считать парные ковариации по всем ценным бумагам. Одноиндексная модель предполагает, что показатели любой ценной бумаги зависят только от выбранного индекса, его доходности и риска.

Заметим, что риск отдельной ценной бумаги портфеля раскладывается на две составляющих – риск, связанный с колебаниями портфеля в целом, нестабильностью всего рынка, и риск случайной ошибки регрессионного уравнения, то есть неустойчивости самой бумаги:

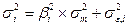
Разделим обе части равенства на 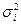. Получим:

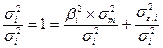
Первое слагаемое показывает, какую долю в суммарном риске ценной бумаги можно описать с помощью регрессионной модели, а какую следует приписать ее неточности.

Мы рассчитали среднеарифметическую доходность и дисперсию каждой ценной бумаги на рынке. Теперь мы можем определить ожидаемую доходность и риск портфеля, состоящего, например, из 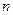ценных бумаг.

Математическое ожидание доходности портфеля из 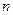ценных бумаг представляется следующим образом:

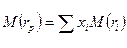, где

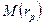- математическое ожидание доходности портфеля из 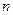ценных бумаг;

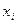- доля 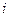-й ценной бумаги в портфеле из 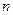ценных бумаг;

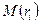- математическое ожидание доходности 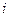-й ценной бумаги.

Подставим в эту формулу выражение для математического ожидания 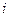-й ценной бумаги:

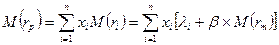
Разделим слагаемые на две части, зависимую и не зависимую от рынка:

.

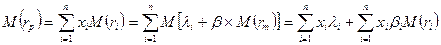Для упрощения записи мы можем представить рыночный индекс как показатель условной 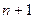ценной бумаги.

Для этого введем следующее:

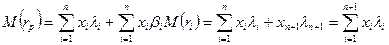, где

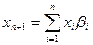и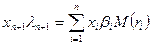

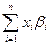- портфельная «бета»

Дисперсия портфеля из 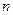ценных бумаг:

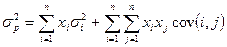
Подставим в формулу выражения, полученные ранее, а именно:

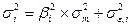
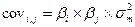
Получим, с учетом условного введения 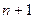ценной бумаги:

.

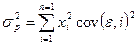При этом

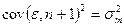и

Сформулируем одноиндексную модель У. Шарпа в целом в сравнении с моделью Г. Марковица.

Модель Г. Марковица:

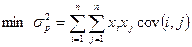
При условиях:

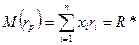
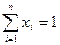
Одноиндексная модель У. Шарпа

.

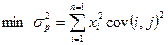При условиях:

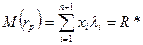
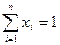
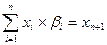
Модель Тобина

Для дальнейшего упрощения задачи выбора были введены новые допущения. В частности, Тобин Дж. предположил возможность инвестиций в безрисковый актив. Введение безрискового актива существенно меняет конфигурацию допустимого и эффективного множества инвестиционных портфелей

Свойства рынка капитала, принятые в теории инвестиционного портфеля с наличием безрискового актива, частично повторяют предпосылки модели Г. Марковица.

1. Все инвесторы, хотя бы в неявной форме, при осуществлении выбора своих капиталовложений ориентируются на теорию инвестиционного портфеля. Каждый индивидуум исходит в своих решениях только из прогнозов:

- ожидаемой доходности;

- дисперсий доходности;

- корреляции между доходностями из различных источников.

2. Отсутствуют какие-либо трансакционные издержки и налоговые обязательства, связанные с инвестициями.

3. На рынке существует консенсус относительно перспективы каждой продаваемой и покупаемой ценной бумаги

4. Существуют активы, полностью лишенные риска.

Предположим, что инвестор, обладающий только безрисковыми ценными бумагами, рассматривает вложение части своих средств в приобретение портфеля В, состоящего из набора рисковых ценных бумаг. Если он вложит в портфель В 10% своего капитала, то он сможет ожидать среднюю доходность, равную:

.

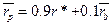Риск, связанный с получением такой доходности будет равен, исходя из формулы суммы дисперсий с учетом весов ценных бумаг, нулевых дисперсии безрисковой ценной бумаги и ковариации безрисковой ценной бумаги с рисковым портфелем:

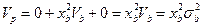
или

или

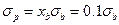
Если инвестор 50% своего капитала в рисковый портфель, то доходность и риски станут:

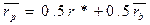
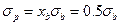
Дополнительная доходность на единицу риска может быть найдена путем деления изменения доходности на изменение общего риска.

В первом случае такой расчет дает:

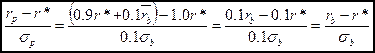
Аналогичный результат получается и для второго случая (50%).

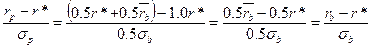
Итак, мы приобретаем дополнительный доход за счет получения дополнительного риска.

Таким образом, общая доходность безрисковой ценной бумаги и портфеля рисковых ценных бумаг может быть представлена следующим образом:

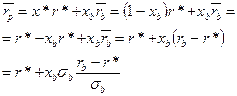
или

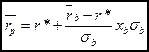
Эта прямая линия 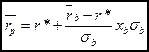называется линией рынка капитала.

Выражение 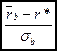можно рассматривать как рыночную цену риска. Или иначе, можно сказать, что необходимый доход от любой комбинации безрисковой ценной бумаги и портфеля рисковых ценных бумаг может быть определен как:

,

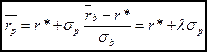где

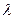- рыночная цена риска.

Рис. 12. Связь доходности и риска портфеля в модели Тобина

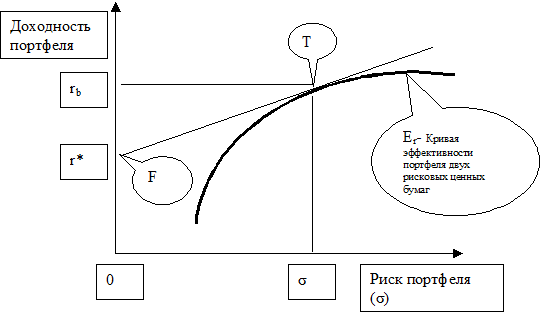
Приведем более формальное изложение проблемы. Предположим, что эффективное множество 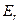состоит только из рискованных ценных бумаг .

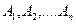Также на рынке существует безрисковый актив .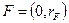

В силу вогнутости множества 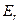существует не более одной касательной к множеству 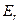, проходящей через точку .

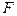Рассмотрим случай существования касательной. Обозначим ее через 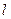, а точку касания – через .

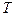Теорема 1. Луч 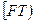является допустимым и эффективным множеством портфелей, состоящих из бумаг .

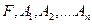Доказательство.

Исследуем множество допустимых портфелей. Пусть

,

,

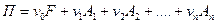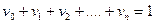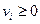при .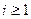

Через 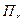обозначим портфель, состоящий только из рискованных ценных бумаг 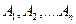, доли которых такие же, как и в портфеле 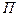. В этом случае 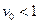. Легко подсчитать, что

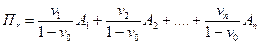
Тогда

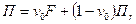
Ожидаемые доходность и риск портфеля 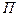равны:

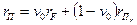
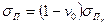(1)

Так как 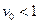, то полученные параметрические уравнения (1) для 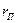и 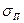задают луч на плоскости 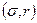. Следовательно, портфель 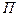находится на луче .

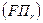Портфель 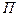, состоящий из бумаг 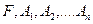, является допустимым тогда и только тогда, когда существует допустимый портфель 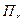(то есть портфель с доходностью 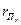и риском 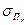) такой, что .

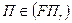Дело в том, что приобретение безрисковой бумаги допустимо по первоначальному допущению, а ввиду выпуклости допустимого множества точки, лежащие на отрезке, проходящем через допустимые точки множества, также допустимы. Если предположить возможность не только покупки, но и выпуска безрисковых ценных бумаг, то допустимы все точки на луче, проходящем через две допустимые точки.

Другими словами, точка 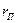, 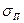является допустимой, если допустимы точк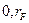и и .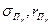

Значит, портфели, лежащие на луче 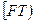, являются допустимыми, так как 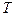- допустимый портфель, состоящий только из рискованных ценных бумаг.

Теперь покажем, что любой портфель, лежащий на луче 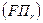, является и эффективным.

Предположим, что допустимый портфель 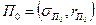, лежащий на луче 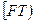, не является эффективным. Тогда существует другой портфель 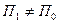такой, что 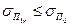и 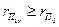. Из этого следует, что 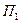находится левее и выше луча 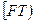. По доказанному существует портфель 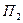, состоящий только из рискованных ценных бумаг, такой, что 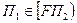. Таким образом, получается, что луч 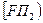находится левее и выше луча 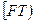. Но в этом случае луч 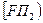не может пересекать множество допустимых портфелей, так как портфель 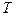является по условию касательным портфелем.

Теорема 2. (теорема разделения). Предполагается, что инвесторы одинаково оценивают риски и ожидаемые доходности ценных бумаг. Тогда оптимальная для инвестора комбинация рискованных активов не зависит от его предпочтений относительно риска и дохода.

Доказательство.

По теореме 1 все инвесторы сформируют портфель 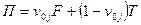. Этот портфель является допустимым и эффективным.

У различных инвесторов 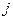могут быть различные доли безрисковых бумаг 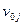. Но структура портфеля рискованных ценных бумаг у всех инвесторов должна быть одинаковой, так как касательный портфель для всех один (портфель ).

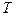Теорема 3. Предположим, что существует точка 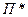касания индивидуальной кривой безразличия некоего инвестора и эффективного множества портфелей. Тогда оптимальный портфель для выбранного инвестора находится в точке .

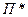Следует ли из этого, что все инвесторы сформируют один и тот же портфель? Нет, не следует. Чем больше инвестор не расположен к риску, тем ниже на луче 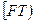будет расположен его оптимальный портфель (то есть, тем больше средств он потратит на безрисковую часть своего портфеля).

Таким образом, мы нашли геометрический способ нахождения оптимального портфеля. Строится множество допустимых портфелей, затем выделяется множество эффективных. Затем из точки безрискового портфеля проводится касательная к эффективной кривой. На этом луче и располагаются оптимальные портфели разных инвесторов. Их различное отношение к риску проявляется в том, что они располагаются ближе или дальше от точки безрискового актива.

Приведем аналитический подход к решению задачи.

Пусть 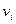- это доля ценной бумаги 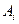в произвольном портфеле ,

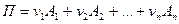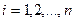
Тогда цель инвестора – выбрать доли 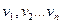так, чтобы значение функции 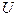на получившемся портфеле 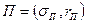было наибольшим:

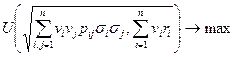
При

,

.

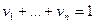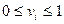Условие 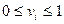означает, что ценные бумаги запрещено брать взаймы и давать в долг. Если на рынке существует безрисковая бумага 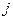, которую можно не только покупать, но и выпускать, то данное условие для соответствующей доли 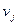должно быть опущено.