Правила записи приближенных чисел

Пусть приближенное число a^* задано в виде конечной позиционной записи:

,

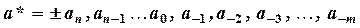где a_j – десятичные цифры .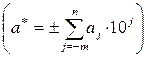

Первая слева, отличная от нуля цифра данного числа, и все расположенные справа цифры называются значащими. Например, числа 537,243 и 0,3470 имеют соответственно 6 и 4 значащие цифры.

Цифра a_j называется верной в широком смысле, если 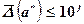, т.е. абсолютная погрешность числа a^* не превосходит одной единицы соответствующего разряда десятичного числа.

Цифра a_j называется верной в узком смысле, если 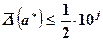, т.е. абсолютная погрешность числа a^* не превосходит половины одной единицы соответствующего разряда десятичного числа.

В известных таблицах Брадиса значения синуса даны с абсолютной погрешностью £ 0,5 × 10^-4, т.е. с четырьмя верными значащими цифрами в узком смысле.

В последнее время стали использоваться таблицы (таблицы различных физических величин, экспериментально составленные таблицы), в которых абсолютные погрешности не превосходят единицы последнего разряда, т.е. используются только верные значащие цифры в широком смысле.

Пример. Для точного числа a = 17,976 число a^* = 17,97 является приближенным с четырьмя верными цифрами в широком смысле, т.к. 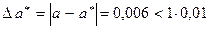, но 0,006>0,5·0,01. Или a^* = 17,98 является приближенным с четырьмя верными цифрами в узком смысле, т.к. .

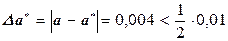При записи приближенного числа выписываются только его верные знаки (цифры). При этом на правом конце выписываются и верные нули. Например, числа 0,045 и 0,0450, как приближенные, различны. Первое число – с абсолютной ошибкой £ 10^-3, второе – с абсолютной ошибкой £ 10^-4 (если говорить о верных цифрах в широком смысле).

При записи приближенных чисел могут встретиться случаи, когда значащих цифр больше, чем имеется верных знаков.

Рассмотрим число a^* = 560000. Известно, что у него верными являются четыре цифры. Но нули мы здесь отбросить не можем, так как изменится число. В этом случае число записывают в нормализованном виде, т.е.

a^* = 560000 = 0,5600 × 10⁶.

В дальнейшем подобные записи (такие как а^* = 560000 при числе верных знаков, меньших шести) не допустимы, если число верных знаков меньше значащих. Надо переходить к записи в нормализованном виде.

Часто употребляют запись вида

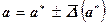, (2.11),

означающую, что неизвестная величина а удовлетворяет неравенствам

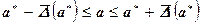. (2.12).

При этом величина 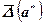выписывается с одной или двумя значащими цифрами, а младший разряд в а^* соответствует младшему разряду в .

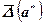Например, верна запись

a = 2,730 ± 0,017. (2.13).

Следующие записи не верны

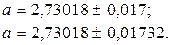
Можно говорить о числе верных значащих цифр у приближенного числа и о числе верных цифр после запятой. Как правило, при реальных вычислениях у приближенных чисел содержатся цифры после запятой, т.е. имеется дробная часть.

Например, приближенное число а^* = 33,277 имеет пять верных значащих цифр и 3 верные цифры после запятой, а у числа b^* = 0,00305 – три верные значащие цифры и 5 верных цифр после запятой.

Очевидно следующее утверждение: «Абсолютная погрешность приближенного числа вполне характеризуется числом верных цифр после запятой, а относительная погрешность – числом верных значащих цифр».

Округление чисел

При вычислениях часто возникает необходимость округления чисел, т.е. представления их с меньшим числом разрядов.

Правило округления чисел. Если в старшем из отбрасываемых разрядов стоит цифра меньше пяти, то содержимое сохраняемых разрядов числа не изменяется. В противном случае в младший сохраняемый разряд добавляется единица с тем же знаком, что и у самого числа. Если первая слева из отброшенных цифр равна 5 и за ней не следуют отличные от нуля цифры, то последняя оставшаяся цифра усиливается, если она нечетная, и остается без изменения, если она четная (правило четной цифры).

Пример: 5,785 » 5,78; 5,775 » 5,78.

Очевидно, что погрешность, возникающая при таком округлении, не превышает по абсолютной величине половины единицы младшего оставляемого знака.

Повторное округление не рекомендуется. В некоторых случаях это может привести к увеличению погрешности.

Пример: 18,33461 » 18,335 » 18,34

или 18,33461 »18,33.

Видно, что при двукратном округлении получилась абсолютная погрешность 0,00539. При однократном – 0,00461.

В ЭВМ применяется такое правило округления, хотя в некоторых случаях цифры, выходящие за разрядную сетку, просто отбрасываются. В этом случае максимально возможная погрешность результата выполнения операции в два раза больше по сравнению со случаем округления. Это очевидно из следующих примеров:

1) 13,5½99 » 13,5 ® когда младшие разряды отбрасываются;

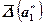= 0,099 » 0,1 (пример максимальной ошибки (в широком смысле)).

2) 13,5½49 » 13,5 ® когда округляют по приведённому выше правилу;

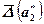= 0,049 » 0,05(тоже пример максимальной ошибки (в узком смысле)).

Видим, что

.

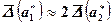В современных машинах предусмотрена свобода выбора способа округления.

На практике округляют постоянные, известные с большим числом знаков, произведения многозначных чисел, частные от деления и т.д. Например, при умножении двух приближенных чисел, имеющих по шесть верных значащих цифр, результат получается с 11 или 12 значащими цифрами.

Правила подсчета цифр (Брадиса).

При вычислениях, если не проводится строгий подсчет погрешностей, рекомендуется пользоваться правилами подсчета цифр. Эти правила указывают, как следует проводить округление всех результатов, чтобы, во-первых, обеспечить заданную точность окончательного результата и, во-вторых, не производить вычислений с лишними знаками, не оказывающими влияния на верные знаки результата.

1. При сложении и вычитании приближенных чисел в результате следует сохранить столько десятичных знаков, сколько их в приближенном данном с наименьшим числом десятичных знаков.

2. При умножении и делении в результате следует сохранить столько значащих цифр, сколько их в приближенном данном с наименьшим числом верных значащих цифр.

3. При возведении приближенного числа в квадрат или куб в результате следует сохранить столько значащих цифр, сколько их в основании степени.

4. При извлечении квадратного и кубического корней из приближенного числа в результате сохранить столько значащих цифр, сколько их в подкоренном числе.

5. При вычислении промежуточных результатов следует сохранить на одну цифру больше, чем рекомендуют правила 1-4. В окончательном результате эта «запасная цифра» отбрасывается.

6. Если некоторые данные имеют больше десятичных знаков (при сложении и вычитании) или больше значащих цифр (при других действиях), чем другие, то их предварительно следует округлить, сохраняя лишь одну «запасную цифру».

7. Если данные можно брать с произвольной точностью, то для получения результата с m верными цифрами исходные данные следует брать с таким числом цифр, которые, согласно предыдущим правилам, обеспечивают (m + 1) цифр в результате.

Имеются следующие правила арифметических действий с приближенными числами:

1) При умножении и делении приближенных чисел, вообще говоря, с различным числом верных значащих цифр производится округление результата с числом значащих цифр, совпадающим с минимальным числом верных значащих цифр у исходных чисел.

2) При сложении и вычитании приближенных чисел, имеющих одинаковое число верных цифр после запятой, округление не производится. При сложении и вычитании приближенных чисел с различным числом верных цифр после запятой результат округляется по минимальному числу верных цифр после запятой у исходных чисел.