Расчет высоты дымовой трубы

Дымовая труба служит для удаления продуктов сгорания из печи. Необходимое разряжение создается в дымовой трубе, т. к. из-за разности плотностей холодного наружного воздуха и горячих газов горячие газы стремятся подняться вверх.

Найдем зависимость разрежения создаваемого трубой, от высоты трубы Н и температуры газов (рис. 1.)

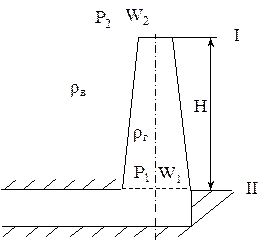
Рисунок 1.

За уровень отсчета принимаем сечение II. Напишем уравнение Бернулли для сечения I и II: Р_геом.1+Р_ст.1+Р_дин.1= Р_геом.2+Р_ст.2+Р_дин.2+Р_пот.

Труба в сечении II сообщается с атмосферой, поэтому Р_ст.2=0.

Тогда Р_ст.1= –Р_геом.1+Р_дин.2 –Р_дин.1+Р_пот

Умножим правую и левую части уравнения на минус единицу:

–Р_ст.1= Р_раз.= Р_геом.– (Р_дин.2 –Р_дин.1)–Р_пот (Следовательно, у основания трубы Р_ст1 отрицательное, т. е. Разряжение)

Р_пот.= Р_тр.+К_м.с×Р_дин.2

На выходе из трубы К_м.с.=1, тогда Р_пот.= Р_тр.+ Р_дин.2

Вследствие этого можно записать:

Р_разр.=Р_геом.+Р_дин.1–2Р_дин.2–Р_тр. (1.37)

Знаем, что , , .

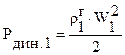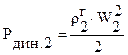Температура газов по высоте дымовой трубе и ее сечение существенно изменяются, поэтому в расчете r и W определяются по средней температуре по высоте трубы для Р_геом. и Р_тр.

.

Подставим в уравнение (1.37) Р_геом., Р_дин.1, Р_дин.2, Р_тр и выразим их через скорости и плотности при нормальных условиях (W₀, r₀):

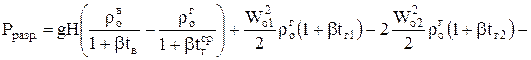
, Па, (1.38)

где 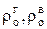– плотность газа и воздуха при нормальных условиях, кг/м³;

d_cр – средний диаметр по высоте трубы, м;

W_o1, W_o2 – скорость газов в сечениях I и II при 0 ⁰С;

W_oср – средняя скорость газов по высоте трубы при 0 ⁰С;

t_в – температура окружающего воздуха, ⁰С;

t_г1 и t_г2 – температура газа в сечениях I и II, ⁰С;

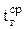– средняя температура газов по высоте трубы, ⁰С;

Если учесть, что 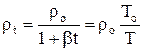; ; 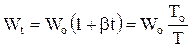где Т_о=273К, то запишем:

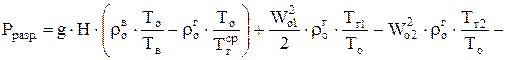
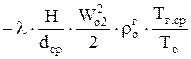. (1.39)

Отсюда определяем высоту дымовой трубы H (м):

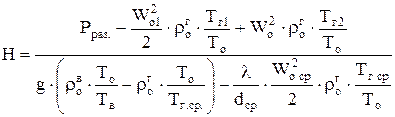. (1.40)

Обычно Р_раз=1,3åР_пот.

Лекция 6:

Сверхзвуковое движение газов

Общие сведения

В металлургических печах иногда применяются такие устройства, в которых газ движется с весьма высокой скоростью, превышающей иногда скорость звука.

Согласно современным представлениям, скорость звука определяют формулой Лапласа, по которой

, (1.41)

где c=С_р/С_v –коэффициент, равный отношению теплоемкости среды при постоянном давлении к теплоемкости при постоянном объеме.

Применяя формулу Клайперона (р/r=RT), получим , где R – универсальная газовая постоянная, 8,3143 кДж/(кмоль*К).

Из этого выражения следует, что скорость звука зависит только от температуры и физических свойств газа.

Скорость газа может быть меньше скорости звука, больше и равна ей. Если скорость движения газа станет равной местной скорости звука, то такая скорость газа W=a называется критической. Сечение потока, в котором достигается это равенство, называется критическим. Критическим называется также давление, плотность и температура в этом сечении.

Отношение скорости движения газа W к местной скорости звука а называют числом (критерием) Маха М:

. (1.42)

При М<1 поток дозвуковой, при М=1 звуковой и при М>1 сверхзвуковой.