Решение систем линейных алгебраических уравнений методом Гаусса
Работа выполняется с использованием палитры программирования системы автоматизации математических вычислений Mathcad
Задание на работу:
1. Разработать программу для решения системы линейных алгебраических уравнений методом Гаусса с выбором главного элемента по столбцам.
2. Решить систему уравнений, определенную вариантом задания.
3. Произвести проверку решения.
4. Изменить матрицу коэффициентов А, сделав систему уравнений линейно зависимой, и проверить работоспособность программы в этом случае.
Варианты заданий .
(Система уравненийв матричной записи имеет видAx = b)
1. A= 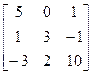 , b=
, b= 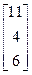 2. A=
2. A= 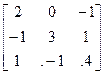 , b=
, b= 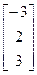
3. A= 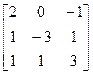 , b=
, b= 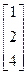 4. A=
4. A= 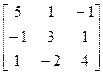 , b=
, b= 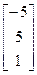
5. A= 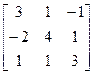 , b=
, b= 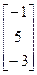 6.A=
6.A= 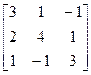 , b=
, b= 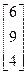
7. A= 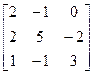 , b=
, b= 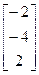 8.A=
8.A= 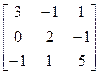 , b=
, b= 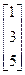
9.A= 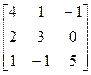 , b=
, b= 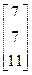 10.A=
10.A= 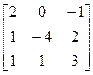 , b=
, b= 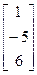
11.A= 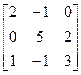 , b=
, b= 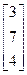 12.A=
12.A= 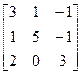 , b=
, b= 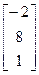
13.A= 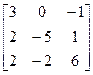 , b =
, b = 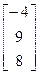 14.A=
14.A= 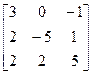 , b=
, b= 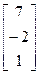
15.A= 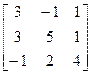 , b =
, b = 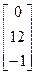 16.A=
16.A= 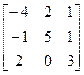 , b=
, b= 
17.A= 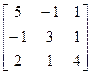 , b =
, b = 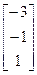 18.A=
18.A= 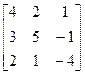 , b=
, b= 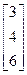
19.A= 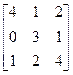 , b =
, b = 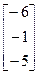 20.A=
20.A= 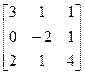 , b=
, b= 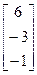
21.A= 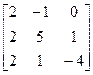 , b =
, b = 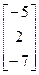
Требования к оформлению отчета
Отчет должен содержать:
- Название и цель работы
- Задание на работу
- Текст программы на Mathcadе
- Результаты работы программы
- Проверку решения
Вспомогательные материалы
Пример разработки программы для решения системы линейных агебраических уравнений в системе Mathcad
Этап 1. Объявление переменных
Определим переменные и зададим матрицу системы линейных уравнений:
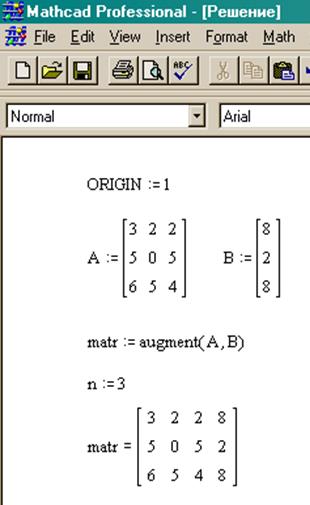 Создадим новый лист в MathCAD и для начала напишем оператор ORIGIN := 1 – это для того чтобы MathCAD начинал нумерацию в матрицах с 1, а не с нуля.
Создадим новый лист в MathCAD и для начала напишем оператор ORIGIN := 1 – это для того чтобы MathCAD начинал нумерацию в матрицах с 1, а не с нуля.
Теперь определим матрицу А.
Обратите внимание, что в MathCAD строчные и прописные буквы различны, следите за регистром переменных.
Наберите A:=нажмите меню Insert è Matrixзадайте размерность матрицы 3 на 3 и нажмите OK. Заполните матрицу как показано на рисунке. Тем же способом задайте матрицу-столбец B.
Объединим все в одну расширенную матрицу matr с помощью оператора augment.
Присвоим переменной nзначение 3, она будет определять количество корней системы.
Чтобы посмотреть значение любой переменной, достаточно написать ее имя и поставить знак равенства. Выведем значение переменной matr.
Еще одной важной особенностью MathCAD является последовательность операторов,например, если мы попробуем написатьвыражениеmatr:=augment(A,B) перед определением матриц A и B, то MathCAD выдаст ошибку.
Переменные определены, теперь перейдем к написанию функции проверки матрицы на линейно-зависимые строки.
Этап 2. Проверка на линейно-зависимые строки
На языке Pascal эта процедура будет выглядеть так:
Function Proverka(): boolean;
var d1: single;
da: word;
lin: boolean;
Begin
d1:=0;
da:=0;
lin:=False;
For i:=0 to n-2 do
Forj:=i+1 to n-1 do
Begin
For k:=0 to n-1 do
If matr[j,k]<>0 then d1:=d1+matr[i,k]/matr[j,k];
d1:=d1/n;
For k:=0 to n-1 do
If matr[j,k]<>0 then If d1=matr[i,k]/matr[j,k] then da:=da+1;
If da=n then lin:=True;
d1:=0;
da:=0;
end;
Iflin then Proverka:=True Else Proverka:=False;
 end;
end;

