Методы интерполирования функций

Работа выполняется с использованием палитры программирования системы автоматизации математических вычислений Mathcad

Задание на работу. В таблице приведены ( в соответствии с вариантами заданий ) значения функций в пяти узлах (с шагом 0.01 ).

1. Найти значения многочлена Лагранжа , интерполирующего функцию f( x ) на заданном отрезке по системе трех равномерно расположенных узлов ( с шагом 0.02 ), в точках (x₀ +x_{2) / 2; (} x₂ + x_{4) /} 2 т. е. в точках x_{1 ,}x ₃ . Полученные результаты сравнить с табличными значениями.

2. Найти значения полинома Ньютона , интерполирующего функцию f( x ) на заданном отрезке по системе трех равномерно расположенных узлов ( с шагом 0.02 ), в точках (x₀ +x_{2) / 2; (} x₂ + x_{4) /} 2 т. е. в точках x_{1 ,}x ₃ . Полученные результаты сравнить с табличными значениями.

3. Построить кубический сплайн отрезке по системе трех равномерно расположенных узлов ( с шагом 0.02 ), в точках (x₀ +x_{2) / 2; (} x₂ + x_{4) /} 2 т. е. в точках x_{1 ,}x ₃

4. Дать оценку точности интерполяции.

Варианты задания

	Номер задания
№	X	e x	e - x	sh x	ch x	sin x	cos x	ln x
	1.00	2.7183	0.3679	1.1752	1.5431	0.8415	0.5403	0.0000
	.01	2.7456	0.3642	1.1907	1.5549	0.8468	0.5319	0.0100
	.02	2.7732	0.3606	1.2063	1.5669	0.8521	0.5234	0.0198
	.03	2.8011	0.3570	1.2220	1.5790	0.8573	0.5148	0.0296
	.04	2.8292	0.3535	1.2379	1.5913	0.8624	0.5062	0.0392

	Номер задания
№	X	e x	e - x	sh x	ch x	sin x	cos x	ln x
	1.05	2.8577	0.3499	1.2539	1.6038	0.8674	0.4976	0.0488
	.06	2.8864	0.3465	1.2700	1.6164	0.8724	0.4889	0.0583
	.07	2.9154	0.3430	1.2862	1.6992	0.8772	0.4801	0.0677
	.08	2.9447	0.3396	1.3025	1.6421	0.8820	0.4713	0.0770
	.09	2.9743	0.3362	1.3190	1.6552	0.8866	0.4625	0.0862

	Номер задания
№	X	e x	e - x	sh x	ch x	sin x	cos x	ln x
	1.10	3.0042	0.3329	1.3356	1.6685	0.8912	0.4536	0.0953
	.11	3.0344	0.3296	1.3524	1.6820	0.8957	0.4447	0.1044
	.12	3.0649	0.3263	1.3693	1.6956	0.9001	0.4357	0.1133
	.13	3.0957	0.3230	1.3863	1.7093	0.9044	0.4267	0.1222
	.14	3.1268	0.3198	1.4035	1.7233	0.9086	0.4176	0.1310

Вспомогательные материалы

1. Пример выполнения работы ( пункт 1 )

Пусть задана функция y = sin xна интервале [ 1.15 , 1.19 ]

X	1.15	1.16	1.17	1.18	1.19
Y	0.9128	0.9168	0.9208	0.9426	0.9284

При задании с шагом 0.2 таблица примет вид:

X	1.15	1.17	1.19
Y	0.9128	0.9208	0.9284

Интерполяционный полином Лагранжа для трех узлов имеет вид

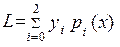
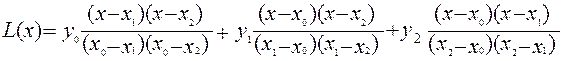
Вычислим по данной формуле значение в точке x = 1.16 . Имеем :

x(0) = 1.15 ; x(1) = 1.17 ; x(2) = 1.19; y(0) =0.9128 ; y(1) = 0.9208; y(2) = 0.9284

Подставляя данные в выражение для L(x), получаем

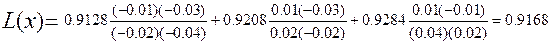
Полученное значение точно совпадает с табличным для x = 1.16.

Оценим погрешность интерполирования по формуле (2). Имеем n = 2.

f ^{(n + 1)} = -cos (x)

Максимальное значение косинуса не превосходит 1. Следовательно, М _{n +1} равно 1.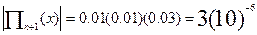

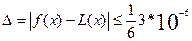= 0.5 * 10 ^{- 6}.

Следовательно, результат интерполирования совпадает с точным значением функции до пяти знаков после запятой.

Разработка программы на Mathcadе трудностей не представляет.

2. Пункт 2 задания выполняется аналогично.

3. Пример Mathcad – программы для построения кубического сплайна приведен ниже.

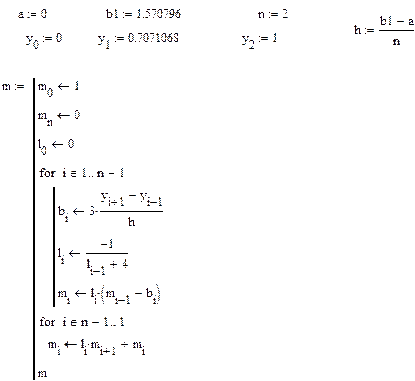
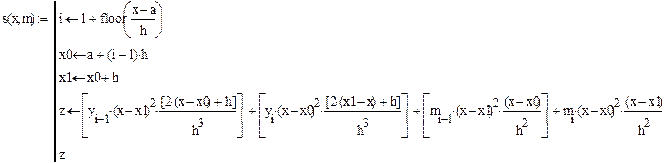
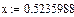
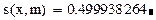
Контрольные вопросы

1.Чему равно значение интерполяционного полинома в узловых точках ?

2. Какова максимальная степень многочлена Лагранжа ?

3. Какова максимальная степень многочлена Ньютона?

4. Как оценивается погрешность интерполяции?

5. В чем состоит различие сплайн – интерполирования от обычной интерполяции?

Раздел 5