Тождественные преобразования выражений

Раскрытие скобок выражения eq осуществляется командой expand(eq). Пример:

> eq:=(x+1)*(x-1)*(x^2-x+1)*(x^2+x+1);

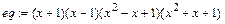
> expand(eq);

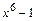
Разложение многочлена на множители осуществляется командой factor(eq).

Пример:

> p:=x^5-x^4-7*x^3+x^2+6*x;

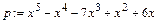
> factor(p);

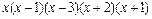
Команда expand может иметь дополнительный параметр, позволяющий при раскрытии скобок оставлять определенное выражение без изменений. Например, пусть требуется каждое слагаемое выражения 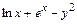умножить на выражение (x+a). Тогда в командной строке следует написать:

> expand((x+a)*(ln(x)+exp(x)-y^2), (x+a));

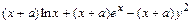
Дробь можно привести к нормальному виду с помощью команды normal(eq). Например:

> f:=(a^4-b^4)/((a^2+b^2)*a*b);

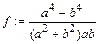
> normal(f);

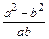
Упрощение выражений осуществляется командой simplify(eq).

Пример:

> eq:=(cos(x)-sin(x))*(cos(x)+sin(x)):

> simplify(eq);

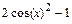
Приведение подобных членов в выражении осуществляется командой collect(exp,var), где exp – выражение, var – имя переменной, относительно которой следует собирать подобные. В команде simplify в качестве параметров можно указать, какие выражения преобразовывать. Например, при указании simplify(eq,trig) будет производиться упрощение при использовании большого числа тригонометрических соотношений. Стандартные параметры имеют названия: power – для степенных преобразований; radical или sqrt – для преобразования корней; exp – преобразование экспонент; ln – преобразование логарифмов. Использование параметров намного увеличивает эффективность команды simplify.

Объединить показатели степенных функций или понизить степень тригонометрических функций можно при помощи команды combine(eq,param), где eq – выражение, param – параметры, указывающие, какой тип функций преобразовать, например, trig – для тригонометрических, power – для степенных. Пример:

> combine(4*sin(x)^3, trig);

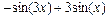
Для упрощения выражений, содержащих не только квадратные корни, но и корни других степеней, лучше использовать команду radnormal(eq). Пример:

> sqrt(3+sqrt(3)+(10+6*sqrt(3))^(1/3))=

radnormal(sqrt(3+sqrt(3)+(10+6*sqrt(3))^(1/3)));

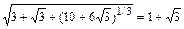
С помощью команды convert(exp, param), где exp – выражение, которое будет преобразовано в указанный тип param. В частности, можно преобразовать выражение, содержащее sinx и cosx, в выражение, содержащее только tgx, если указать в качестве параметра tan, или, наоборот, tgx, ctgx можно перевести в sinx и сosx, если в параметрах указать sincos.

Вообще, команда convert имеет более широкое назначение. Она осуществляет преобразование выражения одного типа в другой. Например: convert(list, vector) – преобразование некоторого списка list в вектор с теми же элементами; convert(expr, string) – преобразование математического выражения в его текстовую запись. Для вызова подробной информации о назначении параметров команды convert следует обратиться к справочной системе, набрав convert[termin].

Если вы забыли параметры какой-либо команды, то можно воспользоваться справочной системой Maple. Для вызова справки по конкретной команде, следует выделить набранное имя этой команды и нажать клавишу F1. Если команда набрана правильно, то появится описание этой команды (в большинстве версий Maple помощь на английском языке).

Задание 4.

1. Перейдите в текстовый режим и наберите «Задание №4». После не забудьте перейти в режим командной строки. Перед выполнением каждого пункта этого задания обязательно набирайте команду обновления restart;

2. Разложить полином на множители 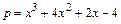. Для этого наберите в командной строке:

> factor(x^3+4*x^2+2*x-4);

После нажатия клавиши Enter должно получиться .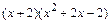

3. Упростить выражение 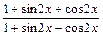. Наберите:

> eq:=(1+sin(2*x)+cos(2*x))/(1+sin(2*x)-cos(2*x)):

> convert(eq, tan):

> eq=normal(%);

.

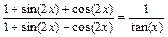4. Упростить выражение 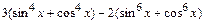. Для этого наберите:

> eq:=3*(sin(x)^4+cos(x)^4)-2*(sin(x)^6+cos(x)^6):

> eq=combine(eq, trig);

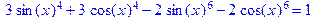
5. Выполните все контрольные задания. Перед их выполнением не забудьте набрать в текстовом режиме «Контрольные задания». Результаты выполнения заданий покажите преподавателю.

6. Сохраните файл со всеми выполненными заданиями на диск.

7. Ответьте на все контрольные вопросы.

Контрольные задания.

При выполнении контрольных заданий студенту необходимо подставить вместо буквенных параметров индивидуальные анкетные характеристики:

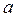- число букв в фамилии студента,

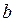- число букв в полном имени студента,

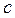- число букв в отчестве студента.

В отчете на титульном листе необходимо обязательно указать, какие анкетные данные использовались при выполнении контрольных заданий (имя, отчество, фамилия).

1. Записать выражение и найти его значение при индивидуальном значении параметра a: .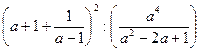

2. Записать дробь и выделить у нее числитель и знаменатель: .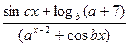

3. Записать точное и и вычислить приближенное значения выражения .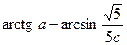

4. Записать формулы: ; .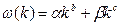

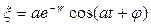5. Раскрыть скобки .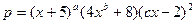

6. Преобразовать в выражение, содержащее только функцию тангенс: .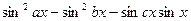

Контрольные вопросы.

1. Что такое Maple и для чего он предназначен?

2. Опишите основные элементы окна Maple.

3. На какие условные части делится рабочее поле Maple и что в этих частях отображается?

4. Как перевести командную строку в текстовую и наоборот?

5. В каком режиме проходит сеанс работы в Maple?

6. Перечислите пункты основного меню Maple и их назначение.

7. Какое стандартное расширение присваивается файлу рабочего листа Maple?

8. Как представляются в Maple основные математические константы?

9. Опишите виды представления рационального числа в Maple.

10. Как получить приближенное значение рационального числа?

11. Какими разделительными знаками заканчиваются команды в Maple и чем они отличаются?

12. Какой командой осуществляется вызов библиотеки подпрограмм?

13. Объясните назначение команд factor, expand, normal,simplify,combine, convert.