Теплопроводность плоских стенок
1.2.1 Теплопроводность однослойной плоской стенки
Рассмотрим однородную плоскую стенку с толщиной 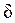 , м и коэффициентом теплопроводности материала стенки
, м и коэффициентом теплопроводности материала стенки 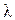 , Вт/(м×К), представленную на рисунке 1.1.
, Вт/(м×К), представленную на рисунке 1.1.
Температурное поле в плоской стенке одномерное, а его градиент направлен по нормали к стенке, совпадающей с осью х. Изотермические поверхности в этом температурном поле представляют собой плоскости, параллельные наружным поверхностям стенки. Температура на левой поверхности стенки во всех точках равна tст1, на правой – tст2. Приняв, tст1> tст2, получим, что поток тепла направлен от tст1к tст2, и его величина  постоянна для всей стенки, так как площадь всех изотермических поверхностей одинаковая.
постоянна для всей стенки, так как площадь всех изотермических поверхностей одинаковая.
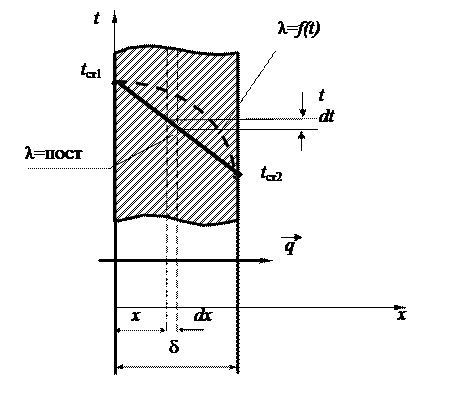
Рисунок 1.1 – Схема температурного поля однослойной плоской стенки
Установим начало координат на левой поверхности стенки и выделим на расстоянии 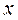 две изотермические поверхности на расстоянии
две изотермические поверхности на расстоянии 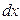 друг от друга при изменении температуры на величину
друг от друга при изменении температуры на величину 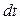 .
.
Уравнение теплопроводности (закон Фурье) для слоя 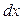 будет иметь вид:
будет иметь вид:
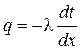 . . | (1.3) |
Принимая 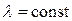 , получим дифференциальное уравнение первой степени с разделяемыми переменными, из которого, разделяя переменные, получим:
, получим дифференциальное уравнение первой степени с разделяемыми переменными, из которого, разделяя переменные, получим:
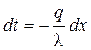 . . |
Интегрируя полученное дифференциальное уравнение, получим уравнение переменной температуры внутри плоской стенки
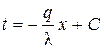 . . | (1.4) |
Из полученного уравнения следует, что при 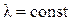 температура внутри плоской стенки изменяется по линейному закону (рисунок 1.1).
температура внутри плоской стенки изменяется по линейному закону (рисунок 1.1).
Постоянная интегрирования 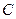 находится из граничных условий:
находится из граничных условий:
– при х = 0, t = tст1;
– при х = 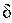 , t = tст2.
, t = tст2.
Подставляя первое граничное условие, имеем
С = tст1 и 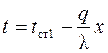 . . | (1.5) |
Подставляя второе граничное условие, получим уравнение вида
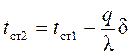 . . |
Решая полученное уравнение относительно величины 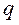 , получим зависимость для определения теплового потока через плоскую стенку
, получим зависимость для определения теплового потока через плоскую стенку
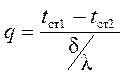 . . | (1.6) |
Обозначим величину 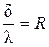 , К·м²/Вт и назовем ее термическим сопротивлением плоской стенки, тогда уравнение теплового потока для плоской стенки примет вид:
, К·м²/Вт и назовем ее термическим сопротивлением плоской стенки, тогда уравнение теплового потока для плоской стенки примет вид:
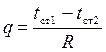 . . | (1.7) |
Уравнение теплопроводности в таком виде аналогично закону Ома для проводника, где тепловой поток  соответствует силе тока, (
соответствует силе тока, ( 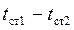 ) – разности потенциалов – движущей силе процесса, а R – электрическому сопротивлению.
) – разности потенциалов – движущей силе процесса, а R – электрическому сопротивлению.
Для строительных и теплоизоляционных материалов, для которых  определяется уравнением (1.2), уравнение теплопроводности будет иметь вид:
определяется уравнением (1.2), уравнение теплопроводности будет иметь вид:
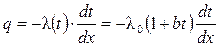 . . | (1.8) |
Разделяя переменные, получим выражение
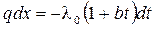 , , |
из которого после интегрирования получим
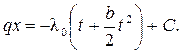 | (1.9) |
Определяем постоянную интегрирования из принятых граничных условий. После подстановки первого условия приходим к выражению вида
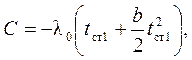 | (1.10) |
откуда
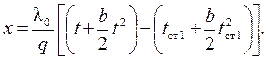 | (1.11) |
Из уравнения (1.9), подставляя значение С, имеем:
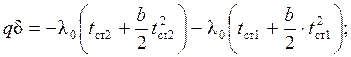 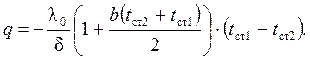 | (1.12) |
Если представить величину 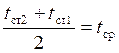 , то приходим к выражению
, то приходим к выражению
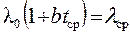 , и , и 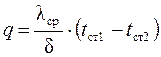 , , | (1.13) |
Из уравнения (1.11) следует, что, заменяя 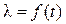 величиной
величиной 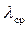 , определенной из уравнения (1.2) по температуре
, определенной из уравнения (1.2) по температуре 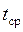 , можно в дальнейшем использовать уравнения (1.5) и (1.6), принимая
, можно в дальнейшем использовать уравнения (1.5) и (1.6), принимая 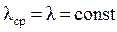 .
.
Переменную температуру внутри плоской стенки 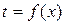 можно найти, решая квадратное уравнение (1.11).
можно найти, решая квадратное уравнение (1.11).
1.2.2 Теплопроводность многослойной плоской стенки
На практике плоская стенка встречается наиболее часто в виде многослойной конструкции с параллельными плотно прилегающими слоями.
Рассмотрим многослойную плоскую стенку, состоящую из 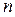 однородных параллельных слоев с толщиной
однородных параллельных слоев с толщиной 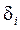 и постоянным коэффициентом теплопроводности
и постоянным коэффициентом теплопроводности 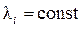 в каждом слое. Температура на наружной поверхности первого слоя во всех точках равна
в каждом слое. Температура на наружной поверхности первого слоя во всех точках равна 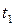 , на поверхности последнего слоя –
, на поверхности последнего слоя – 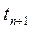 . Тепловой поток
. Тепловой поток 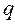 – постоянная величина для всех слоев и направлен в сторону понижения температуры.
– постоянная величина для всех слоев и направлен в сторону понижения температуры.
Схема температурного поля такой многослойной плоской стенки представлена на рисунке 1.2.
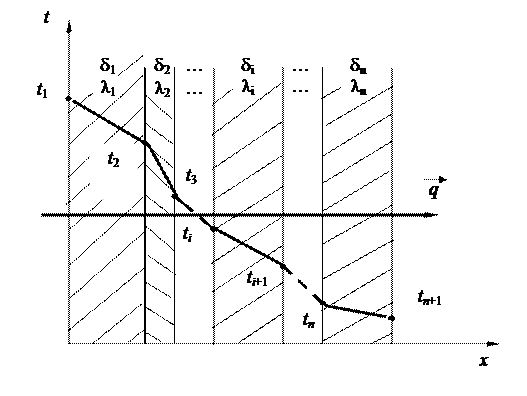 |
Рисунок 1.2 – Схема температурного поля многослойной плоской стенки
Запишем уравнения (1.7) теплового потока при теплопроводности для каждого слоя в отдельности и представим их в виде системы:
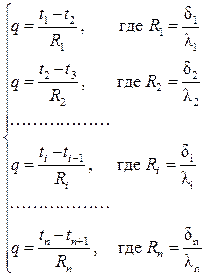
Решая полученные уравнения относительно разности температур и складывая почленно их левые и правые части, после сокращения одинаковых температур с разными знаками, будем иметь:
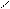


|
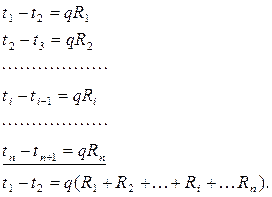
Тогда суммарное уравнение теплового потока для многослойной плоской стенки можно представить в виде:
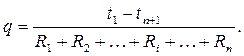 | (1.14) |
Обозначим выражение в знаменателе как
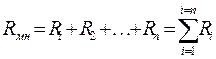 | (1.15) |
и назовем его – термическое сопротивление многослойной стенки. Тогда уравнение теплового потока окончательно примет вид:
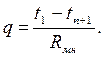 | (1.16) |
По аналогии с последовательным соединением электрических проводников, термическое сопротивление многослойной стенки равно сумме термических сопротивлений всех ее отдельных слоев.
Для определения температуры в любом промежуточном слое ti+1 используем условие постоянства теплового потока при любом числе слоев в уравнении (9.14)
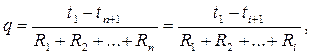 | (1.17) |
откуда получаем выражение:
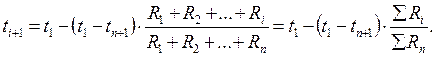 | (1.18) |
Пример решения
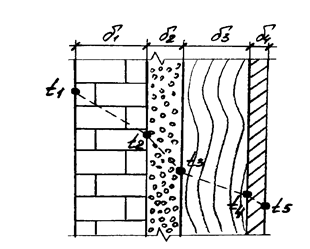 1.1. Последовательность выполнения задания 1.1.
1.1. Последовательность выполнения задания 1.1.
| Рисунок 1 - Эскиз боковой стенки топочной камеры |
d1= l1=
d2= l2=
d3= l3=
d4= l4=
t1= t5=
q0= qм=
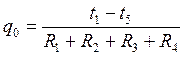 1.1.1. Удельный тепловой поток через многослойную плоскую стенку.
1.1.1. Удельный тепловой поток через многослойную плоскую стенку.
,
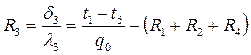 откуда
откуда
,
и требуемое значение толщины изоляционного слоя
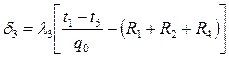
.
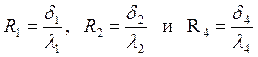 Термическое сопротивление отдельных слоев стенки топки равны
Термическое сопротивление отдельных слоев стенки топки равны
Коэффициенты теплопроводности 1-го и 3-го слоя определяют по средней температуре в данном слое равной
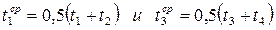
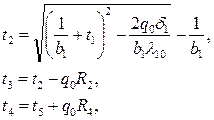 Температуры t2, t3, и t4 определяют из уравнений
Температуры t2, t3, и t4 определяют из уравнений
где - l10 и b1 - коэффициенты в уравнении переменного коэффициента теплопроводности 1-го слоя.
Найденное значение толщины слоя изоляции d3 округляют до ближайшего большего значения, кратного 0,01 м, после чего уточняют фактическое значение величин q0, R1, R3 и температур t2, t3 и t4.
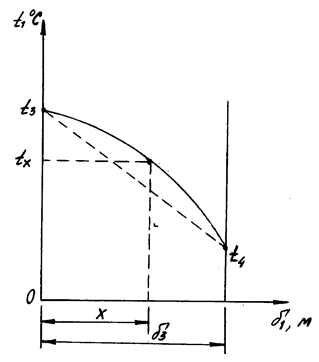 График изменения температуры в слое изоляции d3 (Рис. 2) строится по уравнению
График изменения температуры в слое изоляции d3 (Рис. 2) строится по уравнению
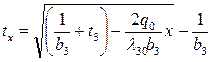 ,
,
,
где х, текущая координата в слое от
х=0 до х=d3, м;
tх, переменная температура в слое, от tх=t3 до tх=t4;
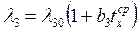 l30 и b3 - коэффициенты в уравнении переменного
l30 и b3 - коэффициенты в уравнении переменного
Рисунок 2 – График изменения температуры
коэффициента теплопроводности изоляции , Вт/(м×К)
t3 - температура на наружной поверхностислоя со стороны входа потока тепла q0, °С.
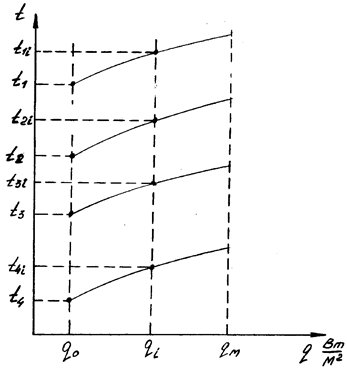
 1.1.2. График изменения температур t1, t2, t3 и t4 (Рис. 3) в зависимости от изменения величины теплового потока от q=q0 до q=qм, строится в следующей последовательности.
1.1.2. График изменения температур t1, t2, t3 и t4 (Рис. 3) в зависимости от изменения величины теплового потока от q=q0 до q=qм, строится в следующей последовательности.
Задается несколько промежуточных значений величин теплового потока qi от qi=q0 до qi=qм.
Для этих величин теплового потока вычисляются промежуточные значения температур t4i, t3i, t2i и t1i в указанной последовательности.
По найденным значениям температур строятся графики ti=f(qi), как показано на Рис. 3. Температуры t1, t2, t3 и t4 при значении qi=q0 , берутся из предыдущего расчета.
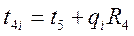 В расчетах используются следующие уравнения:
В расчетах используются следующие уравнения:
;
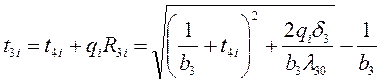
;
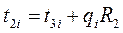
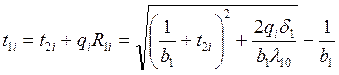
Для построения плавных кривых изменения температур необходимо принимать не менее 3-4 промежуточных значения qi.
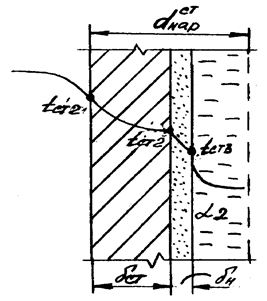
Рисунок 3 – Изменения температур
Рисунок 4 – Эскиз разреза стенки парогенерирующей трубы и график температуры в ней
ПЗ2 Конвективный теплообмен
