Практическая работа №4. Обработка экспериментальных данных
Предположим, что в результате измерений в процессе экспериментов были получены n пар значений: (x1, y1), (x2, y2), …, (xn, yn). Задача состоит в том, чтобы найти приближенную зависимость y = f(x), значения которой при x = xi(i=1,…,n) мало отличаются от опытных данных yi.
Приближенная функциональная зависимость, полученная на основании экспериментальных данных, называется ЭМПИРИЧЕСКОЙ ФОРМУЛОЙ или уравнением регрессии.
Построение эмпирической формулы состоит из двух этапов: подбора общего вида этой формулы и определения наилучших значений содержащихся в ней параметров.
Общий вид формулы обычно выбирается из геометрических соображений: экспериментальные точки наносятся на график, и примерно угадывается общий вид зависимости путем сравнения полученной кривой с графиками известных функций (многочлена, показательной или логарифмической функции и т.п.).
Когда тип эмпирической формулы выбран, ее можно представить в виде:
y=f(x,a1,a2,…,am).
(1)
где f – известная функция, a1,a2,…,am – неизвестные постоянные параметры, необходимо определить такие значения этих параметров, которые дают наилучшее приближение.
ОТКЛОНЕНИЕМ ei называется разность между значениями эмпирической функции (1) в точках x1 (i =1,…,n) и опытными данными yi :
ei=f(xi,a1,a2,…,am)-yi .
(2)
Задача нахождения наилучших значений параметров сводится к некоторой минимизации отклонений ei.
Запишем сумму квадратов отклонений для всех точек x1, x2,…, xn:
 (3)
(3)
Параметры a1, a2,…, am эмпирической формулы (1) будем находить из условия минимума функции S. В этом состоит метод наименьших квадратов. Минимум функции находим из условия равенства нулю частных производных по всем параметрам:

 …
…  (4)
(4)
Полученные соотношения - система линейных уравнений для опреде-ления неизвестных параметров.
Например, для линейной функции y = ax + b эта система имеет вид:

Решая эту систему уравнений, получаем
 (5)
(5)
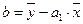 ,
,
где  (6)
(6)
 – значение дисперсии величины X, определяемой по формуле:
– значение дисперсии величины X, определяемой по формуле:

Коэффициент корреляции можно вычислить по формуле:
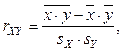
В системе MathCAD существуют встроенные функции для вычисления коэффициентов а и b линейной зависимости y=ax+b:
- slope(x,y) - возвращает значение коэффициента а;
- intercept(x,y) - возвращает значение коэффициента b.
Формулы для вычисления коэффициентов а и b линейной зависимости можно применять для нахождения параметров эмпирических функций, график которых не является прямой линией.
Так, если эмпирическая формула имеет вид степенной функции y=kxm, то, введя обозначения У=lnyиX=lnx можно воспользоваться формулами для вычисления коэффициентов а и b линейной зависимости и выразить через них значения коэффициентов k и m: k=ebиm=a.
Если эмпирическая формула имеет вид показательной функции y=peqx, то, введя обозначения У=lnyиX=x и вычислив коэффициенты а и b линейной зависимости, можно выразить через них значения коэффициентов pиq: p=ebиq=a.

Рисунок 11- Построение эмпирических функций
Задание. По предприятиям промышленности региона получена информация, характеризующая зависимость увеличения объема выпуска продукции (y, %.) от объема капиталовложений (x, млн. руб.).
Требуется:
1. Найти параметры уравнения линейной регрессии (различными способами).
2. Рассчитать коэффициент парной корреляции, коэффициент детерминации.
3. Выполнить прогноз объема выпуска продукции yi при прогнозном значении xi, составляющем 10+№ варианта.
4. На одном графике изобразить исходные данные и теоретическую прямую.
Расчетные данные:
Вариант1
| x | ||||||||||
| y | 18,0 | 23,5 | 38,6 | 47,3 | 85,0 | 99,0 | 105,0 | 140,0 | 157,8 | 185,0 |
Вариант2
| x | ||||||||||
| y | 4,3 | 4,4 | 4,6 | 5,0 | 5,1 | 5,2 | 5,4 | 5,3 | 5,1 |
Вариант3
| x | ||||||||||
| y | 1,7 | 2,0 | 2,4 | 2,9 | 4,2 | 5,1 | 6,2 | 9,2 | 16,6 | 20,2 |
Вариант4
| x | ||||||||||
| y | 2,1 | 2,9 | 3,7 | 4,1 | 4,6 | 5,1 | 5,9 | 6,8 | 7,7 | 6,0 |
Вариант5
| x | ||||||||||
| y | 1,8 | 2,7 | 3,5 | 3,9 | 4,2 | 4,7 | 5,7 | 6,2 | 6,5 | 7,2 |
Вариант6
| x | ||||||||||
| y | 3,9 | 4,3 | 4,6 | 4,7 | 4,8 | 4,9 | 5,0 | 5,1 | 5,45 | 5,5 |
Вариант7
| x | ||||||||||
| y | 2,8 | 4,2 | 5,1 | 5,4 | 5,9 | 7,3 | 6,4 | 7,8 |
Вариант8
| x | ||||||||||
| y | 3,5 | 6,8 | 8,1 | 9,1 | 9,6 | 10,5 | 12,3 | 16,8 |
Вариант9
| x | ||||||||||
| y | 4,1 | 4,2 | 5,3 | 6,1 | 7,2 | 9,2 | 9,9 | 11,5 | 14,3 | 17,6 |
Вариант10
| x | ||||||||||
| y | 5,4 | 6,2 | 6,9 | 7,2 | 7,8 | 8,1 | 9,8 | 10,1 | 9,1 | 9,3 |
Вариант11
| x | ||||||||||
| y | 3,5 | 4,5 | 5,9 | 6,7 | 7,5 | 7,9 | 8,6 | 9,9 | 12,1 | 12,8 |
Вариант12
| x | ||||||||||
| y | 8,1 | 10,2 | 10,8 | 12,3 | 13,1 | 17,4 | 18,7 | 16,9 | 14,8 |
