II. Устные упражнения. III. Тренировочные упражнения по теме урока
№ 554 (б), 765 (а, б, в), 772.
III. Тренировочные упражнения по теме урока.
1. № 747 (в, а), 750, 753, 756 (в), 760.
2. На повторение: № 769, 774, 776 (1, 2).
IV. Итог урока.
Вопросы к п. 19, таблица единиц площади.
V. Домашнее задание. п. 19; № 778, 780 (а), 785, 789 (б).
Урок № 71
Единицы измерения площади (п. 19)
Цели:научить учащихся отвечать на вопрос, какие единицы измерения площадей существуют, переводить одни единицы измерения площадей в другие, использовать знания при решении задач.
Оборудование: ксерокопии тестов.
Ход урока
I. Самостоятельная работа.
| I вариант | II вариант |
| 1. Найти площадь квадрата, сторона которого равна 11 см. 1) 44 см2; 2) 121 см2; 3) 22 см2; 4) 121 см. | 1. Найти площадь квадрата, сторона которого равна 9 см. 1) 18 см2; 2) 81 см2; 3) 81 см; 4) 36 см2. |
| 2. Найти площадь прямоугольника со сторонами 6 см и 4 см. 1) 24 см2; 2) 10 см2; 3) 20 см2; 4) 24 см. | 2. Найти площадь прямоугольника со сторонами 3 см и 10 см. 1) 26 см2; 2) 30 см2; 3) 13 см2; 4) 30 см. |
| 3. Найти периметр прямоугольника, одна из сторон которого равна 9 см, а его площадь – 36 см2. 1) 4 см; 2) 324 см; 3) 13 см; 26 см. | 3. Найти периметр прямоугольника, площадь которого равна 40 см2, а одна из его сторон равна 5 см. 1) 26 см; 2) 8 см; 3) 13 см; 4) 200 см. |
4. Найти площадь фигуры. 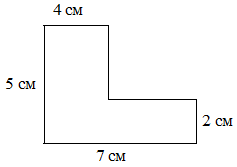 1) 14 см2; 2) 35 см2; 3) 26 см2; 4) 27 см2. | 4. Найти площадь фигуры. 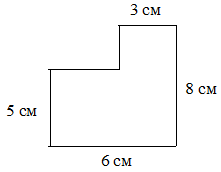 1) 48 см2; 2) 24 см2; 3) 33 см2; 4) 39 см2. |
5. Найти площадь четырех-угольника ABCD. 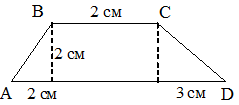 1) 7 см2; 2) 14 см2; 3) 4 см2; 4) 9 см2. | 5. Найти площадь четырёхугольника ABCD.  1) 7 см2; 2) 14 см2; 3) 4 см2; 4) 9 см2. |
(Таблицы учета решений см. в ранее написанных разработках уроков.)
II. Устные упражнения.
№ 763 (в, г, д), 733, 768.
III. Тренировочные упражнения.
1. № 752 (с комментированием с места); № 756 (г), 755, 759.
2. Самостоятельная работа обучающего характера.
а) Площадь поля, имеющего форму прямоугольника, равна 54 га. Найдите ширину этого поля, если его длина 900 м.
б) Площадь земельного участка прямоугольной формы равна 12 а. Ширина участка 30 м. Найдите длину участка.
3. На повторение № 749 (а), 752, 756 (з, и).
IV. Итог урока.
«Догадайся».
Из 10 спичек составлен рисунок ключа (рис. 1). Переложите в нем 4 спички так, чтобы получить 3 квадрата
Ответ: Необходимо снять спички, изображающие кольцо ключа, и расположить их так, как показано на рис. 2
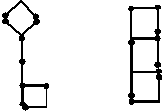
Рис. 1 Рис. 2
V. Домашнее задание. п. 19 повторить; № 770, 773, 777.
Урок № 72
Прямоугольный параллелепипед (п. 20)
Цели:сформировать понятие прямоугольного параллелепипеда, куба, научить находить ребра и грани, вычислять площадь поверхности прямоугольного параллелепипеда.
Оборудование: модели параллелепипеда, куба; плакат с числовым кроссвордом; индивидуальные листы с чертежом для итога урока.
Ход урока
I. Устные упражнения.
Отгадать числовой кроссворд (на столе листок для вычислений).
По горизонтали:
1) Наибольшее четырехзначное число; 2) 103 – 1; 3) Число, показывающее, во сколько раз 3 км 500 м больше 250 м; 6) Наибольшее трехзначное число, записанное цифрами 5, 7 и 9; 7) 88 + 77 + 55 + 44; 9) 10 × 35 × 20 + 2148; 10) Длина всего отрезка, если отрезок разделен на части 12 см, 15 см, 7 см и 14 см; 11) Число минут в двух уроках по 40 минут плюс 10 минут; 13) Число, запись которого римскими цифрами выглядит так: LXIV; 14) Количество сотен в числе 10000; 15)Неизвестное слагаемое в равенстве 71 + х = 96; 17) Число, которое в виде суммы разрядных слагаемых выглядит так: 4 × 1000 + 3 × 10; 18)Число, которое в 3 раза больше числа 203; 19) Самолет пролетел 2100 км за 3 часа. Чему равна его средняя скорость?
По вертикали:
2) Количество сантиметров в 95 м 48 см; 3) Число, на 1 большее, чем 42; 4) Число, которое в виде суммы разрядных слагаемых выглядит так: 4 × 1000 + 5 × 100 + 7 × 10 + 8; 5) Число, которое надо записать в рамочку: 1289071 » 
тыс.; 7) 172; 8) Сколько понадобится трехлитровых банок, чтобы разлить в них 86 л сока? 10) 2002; 12) Сумма числа 5134 и числа, записанного теми же цифрами, но в обратном порядке; 14) Наибольшее из чисел, которое можно подставить в неравенство: + 10 < 148; 16) Неизвестный множитель в равенстве а × 3 = 168; 17) Число 98 в 2 раза больше этого числа.