Их можно разбить на следующие группы: графические, аналитические, приближенные и численные
Графические методыиспользуют геометрические построения. Одним из них, в частности, является метод изоклин для решения дифференциального уравнения первого порядка вида

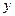 '=
'= 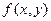 .
.
Он основан на геометрическом определении интегральных кривых по заранее построенному полю направлений, определенному изоклинами (см. ниже).
Аналитические методыприменяются для решения ограниченного круга дифференциальных уравнений, для которых существуют разработанные методы решения. Решения получаются в виде формул в результате аналитических преобразований.
Приближенные методы используют различные упрощения самих уравнений путем обыкновенного отбрасывания некоторых содержащихся в них членов, а также специальным выбором классов искомых функций.
Численные методы решения дифференциальных уравнений в настоящее время являются основным инструментом при исследовании научно-технических задач. Наиболее распространенным и универсальным является метод конечных разностей: область непрерывного изменения аргумента приближенно заменяется функцией дискретного аргумента на заданной сетке. Эта функция называется сеточной. Исходное дифференциальное уравнение заменяется разностным уравнением относительно сеточной функции.
Таким образом решение дифференциального уравнения сводится к отысканию значений сеточной функции в узлах сетки.
Простейшим численным методом решения дифференциального уравнения является метод Эйлера. Его геометрическая интерпретация тесно связана с понятием поля направлений или поля так называемых изоклин. Последнее, в свою очередь, тесно связано с геометрическим представлением общего решениядифференциального уравнения.
Рассмотрим решение дифференциального уравнения
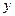 '
' 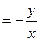 .
.
Мы убедились, что его общим решением является функция 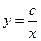 .
.
Если принять 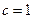 , т.е.
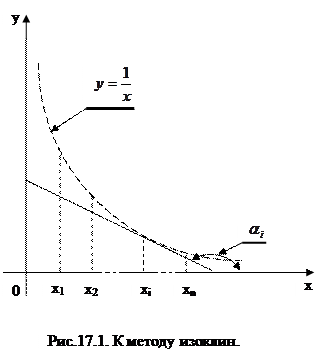
, т.е. 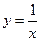 , мы пол учим уравнение гиперболы. Построим штрих-пунктиром график этой функции.
, мы пол учим уравнение гиперболы. Построим штрих-пунктиром график этой функции.
 |
Вспомним, что  '(
'(  ,
,  ) есть не что иное, как тангенс угла наклона касательной, проведенной к кривой
) есть не что иное, как тангенс угла наклона касательной, проведенной к кривой 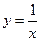 в точке (
в точке (  ,
,  ). Выбрав ряд точек (
). Выбрав ряд точек (  1,
1,  1), (
1), (  2,
2,  2),…,(
2),…,(  n,…,
n,…,  n) на плоскости
n) на плоскости 
 , лежащих на кривой у =
, лежащих на кривой у = 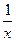 , в каждой из них проведем касательную к этой кривой. При этом для каждой касательной справедливо равенство
, в каждой из них проведем касательную к этой кривой. При этом для каждой касательной справедливо равенство
 '
' 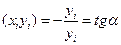 . (17.4)
. (17.4)
В результате мы видим, что дифференциальное уравнение для частного решения дает последовательность касательных, проведенных к кривой, являющейся решением данного уравнения.
Следовательно, для решения дифференциального уравнения достаточно построить в каждой точке плоскости 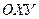 отрезок прямой (касательную), угол наклона которой соответствует дифференциальному уравнению
отрезок прямой (касательную), угол наклона которой соответствует дифференциальному уравнению  '
' 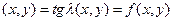 . Совокупность таких отрезков, или направлений, определяет поле направлений . (При этом геометрическое место точек, в которых выполняется соотношение
. Совокупность таких отрезков, или направлений, определяет поле направлений . (При этом геометрическое место точек, в которых выполняется соотношение 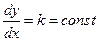 , называется изоклинойданного дифференциального уравнения).
, называется изоклинойданного дифференциального уравнения).
Проведя далее любую кривую в плоскости 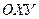 , не пересекающую ни в одной точке ни один из построенных отрезков прямых, мы получим кривую, являющуюся решением данного дифференциального уравнения. Очевидно, что таких кривых можно построить бесконечное множество. Совокупность этих кривых и представляет общее решение данного дифференциального уравнения. Частным решением является кривая, проходящая через точку
, не пересекающую ни в одной точке ни один из построенных отрезков прямых, мы получим кривую, являющуюся решением данного дифференциального уравнения. Очевидно, что таких кривых можно построить бесконечное множество. Совокупность этих кривых и представляет общее решение данного дифференциального уравнения. Частным решением является кривая, проходящая через точку 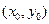 .
.
Пример: Найдем решение дифференциального уравнения
 '
' 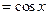
с помощью описанного способа.
Сделаем очевидные преобразования, исходя из геометрического смысла производной:
 '
' 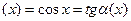 ;
; 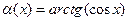 .
.
После этого заполним таблицу, с помощью данных которой построим в плоскости 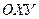 совокупность отрезков с описанными выше свойствами, т.е. поле направлений.
совокупность отрезков с описанными выше свойствами, т.е. поле направлений.

| |
| х | cosx | 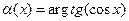 |
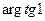 | ||
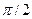 | 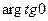 | |
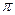 | -1 | 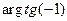 |
3 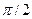 | 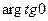 |
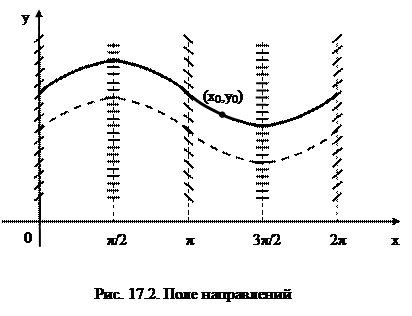 |
Приведенные рисунок и таблица поясняют последовательность построения поля направлений. Из рисунка видно, что решением дифференциального уравнения должна явиться функция 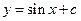 , в чем убеждаемся непосредственной подстановкой. Для нахождения частного решения, соответствующего начальным условиям, проводим кривую через точку (
, в чем убеждаемся непосредственной подстановкой. Для нахождения частного решения, соответствующего начальным условиям, проводим кривую через точку ( 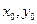 ).
).
Таким образом, обобщая результаты рассмотрения разобранных примеров, мы можем заключить, что с геометрической точки зренияобщий интеграл (общее решение) представляет собой семейство кривых на координатной плоскости, зависящее от одного параметра 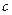 . Эти кривые называются интегральными кривыми данного дифференциального уравнения.
. Эти кривые называются интегральными кривыми данного дифференциального уравнения.
Частному интегралу (или частному решению) соответствует одна кривая этого семейства, проходящая через заданную точку плоскости ( 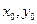 ), определяемую начальными условиями.
), определяемую начальными условиями.
Задача отыскания общего решения дифференциального уравннения с последующим выделением частного решения, соответствующего данным начальным условиям, называется задачей Коши.
