Восходящий разбор: правый анализатор

Автоматы и преобразователи с магазинной памятью: определение МП-автомата,расширенные МП-автоматы

Автоматы с магазинной памятью представляют собой математическую модель синтаксических анализаторов контекстно-свободных языков. В общем случае автомат с магазинной памятью – это односторонний недетерминированный распознаватель, вспомогательная память которого организована по принципу магазина и имеет потенциально неограниченную длину.

МП-автоматом) называется семерка объектов Р=(Q, S, Г, d, q₀, Z₀, F), где Q – конечное множество состояний устройства управления, S – конечный алфавит входных символов, Г – специальный конечный алфавит магазинных символов автомата, d – функция переходов, которая задает отображение множества Q × (S È {e}) × Г в множество конечных подмножеств множества Q × Г^* , q₀ Î Q – начальное состояние устройства управления, Z₀ – начальный символ магазина, FÍQ – множество заключительных состояний.

Расширенным автоматом с магазинной памятьюназывается семерка объектов Р=(Q, S, Г, d, q₀, Z₀, F), где d – функция переходов, которая задает отображение множества Q×(SÈ{e}) × Г^* в множество конечных подмножеств множества Q × Г^*, а все остальные объекты такие же, как и у МП-автомата.

Для расширенных МП-автоматов будем считать, что верхним элементом магазина является самый правый символ цепочки.

Конфигурация расширенного МП-автоматаопределяется так же, как для МП-автомата, и мы можем записать (q, aw, ga) 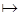(q’, w, gb), если (q’, b) Î d(q, а, a), где q, q’ Î Q, a ÎS È {e}, w ÎS^* и a, b, gÎГ^*. Это означает, что если a¹e, то расширенный МП-автомат при выполнении такта сдвигает входную головку на один символ вправо и заменяет цепочку a, находящуюся в верхушке магазина, на цепочку b.Расширенный МП-автомат может выполнять такты и тогда, когда магазин пуст.

Алгебраические законы для регулярных выражений

Взаимосвязь конечных автоматов и регулярных выражений

Регулярная грамматика G=<N,T,P,S>, правила вывода которой имеют вид: А –> аВ или А–>а, где А,В∈N, а∈Т. Тогда конечный автомат А=<V,Q,δ,q₀,F>, задающий тот же самый язык строится следующим образом: V=T;Q=N U {Z}, Z-заключительное сос-еКА,не принадлежит N и T; q₀= {S}; F={Z} Отображение δ строится по правилам: А–>аВ ставится в соответствие команда (А,а)–>В, а А–>а ставится в соответствие команда (А,а)–>Z. Допустим обратный переход.

Восходящий разбор: правый анализатор

Правый анализатор работает следующим образом:

□ М_r переносит входные символы в магазин, используя функции d, построенные по правилу (2) определения;

□ когда наверху магазина появляется основа, анализатор может свернуть ее, используя функцию d, построенную по правилу (1) определения, и выдать номер правила грамматики, использованного при свертке;

□ М_r продолжает переносить в магазин входные символы до тех пор, пока в его верхней части не появится новая основа, которая свертывается, после чего на выход подается номер соответствующего правила грамматики;

□ преобразователь действует так до тех пор, пока в магазине не останется только начальный символ грамматики с маркером дна магазина. В этом случае, используя правило (3) определения, М_r может перейти в заключительную конфигурацию с опустошением магазина.

Можно доказать, что для КС-грамматики G= (N, S, Р, S)преобразователь М_r, построенный в соответствии с его определением, определяет перевод

t_e(M_r) = {(w, p^r) | S Þ_r^* w}.