Права и обязанности магистрантов-практикантов

МЕСТО ПРАКТИКИ В ООП МАГИСТРАТУРЫ И В СИСТЕМЕ ПЕДАГОГИЧЕСКИХ ПРАКТИК УНИВЕРСИТЕТА.

Педагогическая и научно-педагогическая практики магистрантов, в отличие от педагогической практики бакалавров и студентов-специалистов проводится на базе высшей школы. Содержание практик магистрантов определяется целями комплексного ознакомления с опытом ведущих ученых и преподавателей и нормативными актами системы высшего профессионального образования, а также целями формирования базовых навыков ассистентов профессорско-преподавательского состава при подготовке, проведении и проверке письменных контрольных работ (в формах аналитических вопросов по требуемой тематике, тестовых заданий и проч.) или при подготовке и проведении практических занятий. В отличие от педагогической практики аспирантов, практики магистрантов не предполагают полноформатного участия в учебно-научном процессе и являются студенческой (т.е. не подтвержденной дипломом, допускающим возможность преподавания в высшей школе) формой работы.

Нормы, заложенные в программу научно-педагогической практики магистрантов, представляют собой требования подготовительного этапа в приобретении знаний по работе высшей школы. Эта форма работы тесно связана с последующим возможным этапом активной практической деятельности в рамках аспирантуры — педагогической практики, предусматривающей подготовку и проведение практических занятий (в форме семинаров, коллоквиумов, лабораторных работ и проч.). Таким образом, системность подготовки кадров высшей школы определяется поэтапностью и преемственностью разных ступеней образования.

В ходе педагогической практики студент-магистрант приобретает знания структуры образовательного процесса в системе высшего профессионального образования, овладевает умениями проектирования содержания, планирования, организации и анализа этого процесса; активизирует свои теоретические знания; формирует профессионально-профильные умения и исследовательские навыки, способствующие его самоопределению в качестве преподавателя, а также личностную и профессиональную готовность к осуществлению научно-педагогической деятельности.

ПРАВА И ОБЯЗАННОСТИ МАГИСТРАНТОВ-ПРАКТИКАНТОВ

Магистрант-практикант должен своевременно выполнять все виды работ, предусмотренные программой практики. В том числе:

— организовывать профессионально-ознакомительную деятельность по изучению системы высшего профессионального образования на основе последних достижений научной мысли и современных методов и технологий;

— реализовывать требуемую аналитическую работу с позиций актуальных подходов к преподаванию специальных языковедческих дисциплин и решению междисциплинарных проблем;

— способствовать достижению общих целей образования в современной высшей школе;

— проводить мониторинг уровня подготовки обучающихся;

— совершенствовать свои представления о возрастной психологии и о психологии участников учебного процесса;

— вести необходимую документацию.

Магистрант-практикант имеет право:

— по всем вопросам, возникающим в процессе практики, обращаться к руководителю магистерской программы, кафедральному (групповому) руководителю практики, заведующему выпускающей кафедрой, администрации института и университета;

— обсуждать с лекторами и преподавателями научную, образовательную и психолого-педагогическую проблематику прослушанных лекций и посещенных практических занятий;

— разрабатывать с преподавателями тематику и содержание контрольных работ и/или практических занятий в актуальных для избранной дисциплины формах, а также обсуждать полученные результаты;

— вносить предложения по совершенствованию содержания и организации практики;

— участвовать в конференциях и совещаниях по практике, проводимых в университете;

— пользоваться библиотекой, виртуальным хранилищем электронных ресурсов, специализированными кабинетами и находящимися в них учебно-методическими пособиями.

Каждый магистрант обязан выполнять необходимые виды работы, предусмотренные программой практики, вести документацию (дневник практики, включающий в себя анализ посещенных лекций и практических занятий, занятий и консультаций группового руководителя, внеаудиторной работы и др.), составить итоговый отчет.

4. ХАРАКТЕРИСТИКА АУДИТОРИИ

Практическое занятие по теме «Конечные деформации сплошного анизотропного цилиндра при комбинированном нагружении» проводилось в группе студентов 6 курса ИПМиКН, обучающихся по направлению «Математика и компьютерные науки» (группа 241541/03). На занятии присутствовало 7 человек.

Основными особенностями аудитории следует считать сравнительно одинаковый уровень образования и культуры; одинаковый возраст (22 - 23 года); единство целей (обучение по данной специальности); схожий режим обязательных занятий.

5. ВОЗРАСТНЫЕ ПСИХОЛОГИЧЕСКИЕ ОСОБЕННОСТИ АУДИТОРИИ

Группа 241541/03 студентов имеют примерно одинаковый возраст и уровень образования, стандартный график специальных и обязательных занятий, а также схожие цели обучения по данной специальности. Разный уровень воспитания, культуры и социального положения определяет их неодинаковое отношение к учебному процессу. Отношение к квалифицированному преподавательскому составу и межличностные взаимоотношения внутри группы позволяют коллективу воспринимать материал соответствующим образом. Основы, полученные на предыдущих курсах, позволяют аудитории корректно использовать полученные знания на практике, что говорит о целесообразности проведения практических занятий в дальнейшем.

Юность - важный этап развития умственных способностей: существенно развивается теоретическое мышление, умение абстрагировать, делать обобщения. Происходят качественные изменения в познавательных возможностях: для студентов характерны нестандартный подход к уже известным проблемам, умение включать частные проблемы и более общие. Также характерной чертой студентов младших курсов является склонность преувеличивать свои интеллектуальные способности, уровень знаний и самостоятельности.

В 17-21 год проходит кризис юности, который характеризуется выявлением и подтверждением своей самостоятельности. Кризис проявляется в том, что человек вступает в самостоятельную взрослую жизнь, представления сложившиеся на предыдущем этапе жизни расходятся с реальностью. В течение 1-2 лет студент переживает кризис адаптации, не справляется с требования ВУЗа. Причины этого - разочарование в профессии, в студенческой жизни. Человек уходит от старых налаженных отношений школы, изменяются отношения со сверстниками и взрослыми, отношения с педагогами становятся более формальными. Задается вопрос: «Кто Я?», «Какой смысл в моей жизни?». Закладывается программа жизни на ближайшее будущее. Именно в этом возрасте наиболее интенсивно развивается интеллект, формальное логическое мышление, которое становится ведущим, опережая развитие эмоций.

Психологические функции приобретают знаковые вербальное выражение (поэтому в качестве доступных для понимания студентов становится вербальные и символьные (в виде формул) методы обучения); основными стимулами и орудием становятся знаки, реакции обусловлены логикой отношений между знаками (определение педагогом логики отношений между знаками приводит к пониманию и овладению учащихся). Развивается сознание, сознательная воля (отсюда установка на овладение информацией, если она будет завербована в будущее, повышение внимания к предмету обучения), память, высшие эмоции.

В возрасте 20-25 лет актуальным для человека становится поиск спутника жизни, теснее сотрудничество с людьми, укрепление связей со своей социальной группой. Человек не боится обезличивания, не смешивает свою индивидуальность с другими людьми, появляется чувство близости, единства, сотрудничества, интимности с определенными людьми.

Данному возрасту покорны специфические психологические особенности: близость к людям, стремление к контакту с людьми, желание и способность посвятить себя людям, рождению и воспитанию детей, любовь к работе, удовлетворенность личной жизнью.

6. ОБОСНОВАНИЕ ВЫБОРА МЕТОДОВ ОБУЧЕНИЯ

К методам организации учебно-познавательной деятельности относятся словесные, наглядные, практические и проблемно-поисковые, индуктивные и дедуктивные методы обучения.

Лекции

Продолжают оставаться ведущей формой организации обучения студентов. На лекции реализуется совокупность взаимосвязанных целей: осуществляется передача студентам фундаментальных и прикладных знаний с их теоретическим анализом, продолжается разностороннее развитие и воспитание различных качеств, отношений, взглядов, убеждений, суждений и т.д. Спектр решаемых с ее помощью учебно-воспитательных задач может быть очень широк. Это теоретическая форма обучения, основной метод - устное последовательное изложение содержания материала. Лекция в вузе не сводится к пересказу учебника или других литературных источников. Она представляет личное научно-педагогическое творчество преподавателя в определенной области знаний и всегда носит авторский характер.

Для лекции характерны большой объем учебного материала, фундаментальность, сложность логических построений, доказательств и обобщений. Лекция охватывает все занятие, в ходе которого студенты получают установку и направление для последующей самостоятельной и других форм работы.

В деятельности студентов на лекции преобладает получение, осмысление и дальнейшее применение полученных знаний к решению практических задач. Лекционный метод обучения выполняет функцию углубления знаний, умений. Выделяется несколько этапов, через которые проходит познавательная деятельность студентов:

• Объяснение преподавателя. Этап теоретического изложения работы..

• Восприятие материала. Этап осмысления и краткого конспектирования материала.

В зависимости от места и роли в учебном процессе различают лекции следующих типов: вводные, систематического курса, обзорные, установочные, итоговые. В современном вузе преподаватели обращаются к лекциям следующих типов: классическая, проблемная, монографическая, лекция-дискуссия, лекция вдвоем, лекция с запланированными ошибками, лекция - аудио визуализация.

Практические занятия

Процесс обучения в высшей школе предусматривает практические занятия. Они предназначены для углубленного изучения дисциплины. Их формы разнообразны.

Практические занятия играют важную роль в выработке у студентов навыков применения полученных знаний для решения практических задач совместно с преподавателем. На младших курсах практические занятия проводятся через 2-3 лекции и логически продолжают работу, начатую на лекции.

Структура практических занятий:

• вступление преподавателя;

• ответы на вопросы студентов по неясному материалу;

• практическая часть как плановая;

• заключительное слово преподавателя.

Важнейшей стороной любой формы практических занятий являются упражнения. Основа в упражнении - пример, который разбирается с позиций теории, развитой в лекции. Как правило, основное внимание уделяется формированию конкретных умений, навыков, что и определяет содержание деятельности студентов - решение задач, графические работы, уточнение категорий и понятий науки, являющихся предпосылкой правильного мышления и речи. Проводя упражнения со студентами, специально обращается внимание на формирование способности к осмыслению и пониманию.

Цель занятий должна быть ясна не только преподавателю, но и слушателям. Практические занятия организуются так, чтобы студенты постоянно ощущали нарастание сложности выполняемых заданий, испытывали положительные эмоции от переживания собственного успеха в учении, были заняты напряженной творческой работой, поисками правильных и точных решений. Большое значение имеют индивидуальный подход и продуктивное педагогическое общение. Обучаемые должны получить возможность раскрыть и проявить свои способности, свой личностный потенциал. Поэтому при разработке заданий и плана занятий должен учитываться уровень подготовки и интересы каждого студента группы и не подавляться самостоятельность и инициативы студентов.

На практическом занятии основным направлением был выбран вопрос получения навыков решения систем линейных алгебраических уравнений. Мною диктовались основные определения, соотношения по данной теме, необходимые для решения задач, все необходимые формулы выписывались на доске, приводились конкретные примеры решения задач, подробно разбиралось решение задач из типового расчета. Отдельные студенты задавали вопросы по решению рассматриваемых задач.

7. АНАЛИЗ РЕАЛИЗАЦИИ УЧЁТА ЗАКОНОМЕРНОСТЕЙ КОЛЕБАНИЯ ВНИМАНИЯ И УТОМЛЯЕМОСТИ АУДИТОРИИ

Внимание - это произвольная или непроизвольная направленность и сосредоточенность психической деятельности на каком-либо объекте восприятия.

В зависимости от наличия сознательного выбора направления и регуляции выделяют после произвольное (или вторично непроизвольное), произвольное и непроизвольное.

Непроизвольное внимание (пассивное) - вид внимания, при котором отсутствует сознательный выбор направления и регуляции. Оно устанавливается и поддерживается независимо от сознательного намерения человека. В основе него лежат неосознаваемые установки человека. Как правило, кратковременно, быстро переходящее в произвольное.

Произвольное внимание - психологической особенностью произвольного внимания является сопровождение его переживанием большего или меньшего волевого усилия, напряжения, причем длительное поддерживание произвольного внимания вызывает утомление, зачастую даже большее, чем физическое напряжение.

После произвольное внимание - вид внимания, при котором в наличии сознательный выбор объекта внимания, но отсутствует напряжение, характерное для произвольного внимания. Связано с образованием новой установки, связанной в большей мере с актуальной деятельностью, нежели с предшествующим опытом человека (в отличие от непроизвольного).

Так как внимание выступает стороной познавательных процессов как деятельности, направленной на объект, то, в зависимости от содержания этой деятельности, выделяют:

• внешнее внимание (сенсорно-перцептивное) — обращено на объекты внешнего мира. Необходимое условие познания и преобразования внешнего мира;

• внутреннее внимание (интеллектуальное) — обращено на объекты субъективного мира человека. Необходимое условие самопознания и самовоспитания;

• моторное (двигательное) внимание.

К числу основных характеристик внимания относят объем, избирательность, устойчивость, отвлекаемость, концентрацию, распределение и переключение.

Устойчивость внимания - это способность объекта не отклоняться от направленности психической активности и сохранять сосредоточенность на объекте внимания. Характеристиками устойчивости внимания являются временные параметры длительности сохранения направленности и сосредоточенности психической активности без отклонения от исходного качественного уровня. Необходимым условием устойчивости внимания является разнообразие впечатлений или выполняемых действий, интерес.

Свойством, противоположным устойчивости, является отвлекаемость. Отвлекаемость выражается в колебаниях внимания, которые представляют собой периодические ослабления внимания к конкретному объекту или деятельности.

Поскольку устойчивость внимания более высокая к предмету, по которому предстоит экзамен, то в начале практического занятия студенты были проинформированы о том, что задачи, подобные рассматриваемым на практике, будут включены в экзаменационные билеты. А также было сообщено, что материал им пригодится при выполнении типового расчета.

Для поддержания внимания студентов материал им сообщался разными темпами речи. Основные сведения медленно диктовались, а пояснения к ним были в обычном разговорном темпе. Чтобы студенты меньше утомлялись, я при подготовке практического занятия равномерно распределил основные сведения, которые студенты записывали, и примеры с пояснениями, которые я просто рассказывал. Также для более лучшего понимания процесса решения рассматриваемых задач приходилось напоминать некоторые соотношения из других разделов математики, например из тригонометрии, из интегрального исчисления и т.д.

Со своей стороны я не монотонно диктовал материал, а старался проявлять внимание к аудитории, следить за тем, как студенты успевают записывать материал и понимают ли они сказанное мною. То есть в процессе практического занятия я распределил своё собственное внимание между чтением основных положений и наблюдением за слушателями и за временем.

Когда прошло приблизительно 40 минут практики внимание студентов понизилось. Чтобы студенты немного отдохнули, я предложил им задать мне вопросы по изложенному материалу.

8. ОПИСАНИЕ ПЕДАГОГИЧЕСКИХ ПРИЁМОВ, ИСПОЛЬЗОВАННЫХ В ХОДЕ НЕПОСРЕДСТВЕННОГО ВЗАИМОДЕЙСТВИЯ С АУДИТОРИЕЙ

Для наглядности в ходе лекционно-практического занятия было произведено несколько графических изображений.

Материал практического занятия излагался последовательно. Для обеспечения доступности материала основные определения и формулы формулировались однозначно. При подготовке практического занятия я избегал сложных длинных предложений.

9. АНАЛИЗ САМООРГАНИЗАЦИИ НА ЗАНЯТИИ

При проведении практического занятия я достаточно просто нашел общий язык со студентами, поэтому не возникло особых затруднений при объяснении методов решения рассмотренных задач.

При подготовке к занятию я повторил теоретический и практический материалы, которые я сам изучал на занятиях, а также решил несколько новых примеров по данной теме для большей уверенности в своих силах.

В случае, когда студентам было непонятно какое-то математическое действие, я производил его более медленно и подробно, давая необходимые рекомендации для получения правильного результата.

Итогом проведенного практического занятия стало умение студентов решать рассмотренные задачи, а также получение мною нового опыта - передача знаний новому поколению специалистов.

10. ВЫВОДЫ О ДОСТИЖЕНИИ ЦЕЛИ УЧЕБНОГО ЗАНЯТИЯ

В ходе практического занятия студенты закрепили материал, по которому уже было проведено лекционное занятие. Рассмотрели методы решения определенных задач, научились решать задания из типового расчета.

Материал был изложен доступным языком и был дан своевременно.

ПРИЛОЖЕНИЕ №1

Неголономная система — механическая система, на которую, кроме геометрических, накладываются и кинематические связи, которые нельзя свести к геометрическим (их называют неголономными). Математически неголономные связи выражаются неинтегрируемыми уравнениями. Движение неголономной системы описывается с помощью специальных уравнений движения (уравнения Чаплыгина, Аппеля, Маджи) или уравнений движения, получаемых из вариационных принципов.

Уравнения Эйлера — Лагранжа преимущественно применяются при рассмотрении неголономных систем, однако их значение не ограничивается этими специальными задачами, так как они позволяют в значительной мере упростить форму и процесс составле­ния уравнений движения и в голономных задачах. Отличительной особенностью данных уравнений является тот факт, что вместо обобщённых скоростей вводятся квазискорости, выражающиеся следующим образом: (*),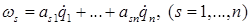

где 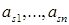- постоянные коэффициенты, 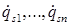- обобщённые скорости.

Будем исходить из общего центрального уравнения (**)

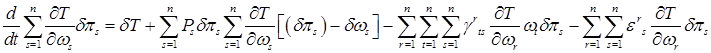
Тре­буется лишь развернуть его левую часть

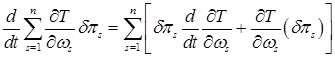(1)

и заменить 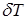в правой части его значением 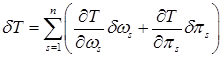(2).

Теперь подстановка в (**) дает

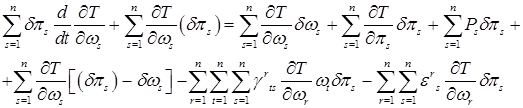(3)

После сокращения приходим к соотношению

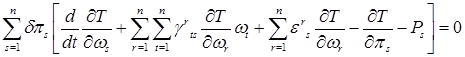(4)

Рассмотрим случаи голономной и неголономной системы по отдельности. В первом случае все вариации 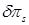независимы и следствием (4) является обращение в нуль коэффициентов при них в этом соотношении. Получаем уравнения движения Эйлера — Лагранжа 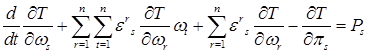, s=1..n (5)

к которым должны быть присоединены кинематические соотношения

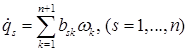(6)

дающие выражения обобщенных скоростей через квазискорости. Получили систему 2n обыкновенных дифференциальных уравнений первого порядка относительно такого же числа неизвестных 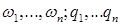(7).

Уравнения упрощаются и принимают вид

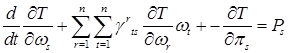(7),

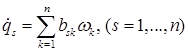(8)

если квазискорости введены с помощью однородных линейных форм с коэффициентами, не содержащими t явно, а не с помощью более общих соотношений.

При наличии неголономных связей в число квазискоростей вносятся линейные формы обобщенных скоростей, обращающиеся в нуль в силу самих уравнений неголономных связей. Последние тогда будут иметь следующий вид:

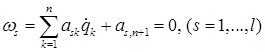(10)

Тогда имеем также

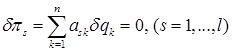(11)

где l - число уравнений неголономных связей. Суммирование по s и t в равенстве (4) поэтому должно производиться от l+1 до n :

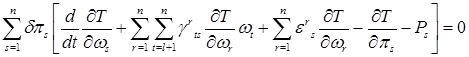(12)

и, поскольку вариации при 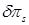независимы, величины в квадратных скобках должны быть нулями. Получаем n-l уравнений движения

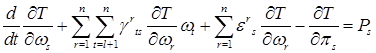, (s = l+1, ... , n) (13)

число которых равно числу степеней свободы. К ним надо присоединить n кинематических соотношений 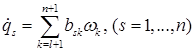(14). Всего имеем 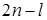уравнений первого порядка, содержащих такое же число неизвестных 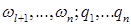(15)

Для составления уравнений (13) достаточно знать лишь те символы 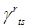, в которых нижние индексы соответствуют номерам квазискоростей, не обращающихся в нуль вследствие уравнений неголономных связей. Уравнения (13) содержат производные кинетической энергии Т по всем квазискоростям, в том числе и по тем, которые,

согласно(10) обращаются в нуль. Поэтому при составлении выражения Т неголономные связи нельзя учитывать, они принимаются во внимание лишь после вычисления производных Т по квазискоростям, т. е. квазиимпульсов .

Можно добавить, что в нем достаточно сохранить лишь линейные относительно квазискоростей слагаемые, т. е. не выписывать произведений и квадратов этих

величин, так как после вычисления квазиимпульсов соответствующие слагаемые все равно отпадут в силу уравнений (10). Отметим еще, что в числе линейных относительно величин 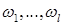слагаемых имеются их произведения на 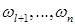. Эти члены, конечно, надо сохранить в выражении Т.

Уравнения движения (5) и (8) обращаются в уравнения Лагранжа, если все квазискорости 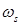являются обобщенными скоростями 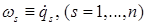(16)

все символы 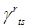и 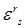будут нулями, а «производные Т по квазикоординатам» станут производными по обобщенным координатам .

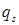Структура выражения кинетической энергии через квазискорости, как правило, гораздо более проста, чем через обобщенные скорости. Этим и объясняется, что уравнения движения в форме Эйлера — Лагранжа оказываются более простыми

по форме и симметричными для значительного класса задач, чем уравнения Лагранжа. Затруднения, связанные с вычислением трехиндексных символов, не столь велики и, во всяком случае, не принципиальны; кроме того, это вычисление при выбранном задании квазискоростей через обобщенные скорости производится один раз навсегда.

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

1. Добронравов В.В. Основы механики неголономных систем / В.В. Добронравов. - М.: Высшая школа, 1970 - 264 с.

2. Беленький И.М. Введение в аналитическую механику / И.М. Беленький. - М.: Высшая школа, 1964 - 324 с.

3. Седов Л.И. Механика сплошной среды. Т.2.: Учебник для университетов / Л.И.Седов. – СПб.: Издательство «Лань», 2004. — 560 с.