Институт сервиса, туризма и дизайна (филиал) в г. Пятигорске

Чебоксаров Александр Борисович

Математический анализ.

Курс лекций

Содержание	Стр
Раздел 1. Введение в математический анализ. Дифференциальное исчисление функций одной переменной.
Лекция 1. Функции одной переменной. Предел функции одной переменной.Понятие функции одной переменной. Способы задания функций. Классификация функций. Область определения функций. Графики функций. Предел функции. Основные теоремы о пределах.
Лекция 2. Бесконечно малые и бесконечно большие функции. Непрерывность функции. Бесконечно малые и бесконечно большие функции. Сравнение бесконечно малых. Некоторые замечательные пределы. Понятие о непрерывности и точках разрыва функций. Свойства непрерывных функций. Классификация точек разрыва.
Лекция 3. Производная функции.Определение производной функции. Ее физическая и геометрическая интерпретация. Таблица производных. Правила дифференцирования. Дифференцирование неявно заданных и параметрически заданных функций. Логарифмическое дифференцирование.
Лекция 4. Дифференциал функции одной переменной. Основные теоремы дифференциального исчисления. Применение основных теорем дифференциального исчисления. Понятие дифференциала функции. Свойства дифференциала. Геометрический смысл дифференциала. Механический смысл дифференциала. Формула Тейлора. Применение формулы Тейлора к вычислению значений функции. Применение дифференциала к приближённым вычислениям.Теоремы Ферма, Ролля, Лагранжа, Коши. Формула конечных приращений. Правило Лопиталя.
Лекция 5. Производные и дифференциалы высших порядков. Исследование функций и построение графика функции. Применение производной функции.Производные высших порядков. Дифференциалы высших порядков. Признаки монотонности функции. Отыскание точек экстремума. Выпуклость, вогнутость графика функции. Точки перегиба. Понятие о асимптотах графика функции.Правила отыскания асимптот. Общая схема исследования функций и приёмы построения графиков. Применение производной в физике. Задачи нахождения минимумов (максимумов).
Раздел 2. Интегральное исчисление функций одной переменной.
Лекция 6. Неопределенный интеграл. Основные методы интегрирования. Понятие первообразной функции и неопределенного интеграла. Основные свойства, таблица. Рассмотрение основных методов интегрирования.
Лекция 7. Интегрирование рациональных дробей. Интегрирование тригонометрических и иррациональных функций. Интегрирование простейших рациональных функций. Метод неопределённых коэффициентов. Выделение целой части в неправильной рациональной дроби. Интегрирование простейших тригонометрических и иррациональных функций. Интегралы, зависящие от радикалов.
Лекция 8. Определенный интеграл. Методы вычисления определенного интеграла.Понятие определенного интеграла и условия его существования. Свойства определенного интеграла. Формула Ньютона- Лейбница. Метод непосредственного интегрирования в определенном интеграле. Замена переменной в определенном интеграле. Метод интегрирования по частям в определенном интеграле.
Лекция 9. Приближённое вычисление определенного интеграла. Несобственные интегралы.Формулы прямоугольников, трапеций Симпсона (параболических трапеций). Интегралы с бесконечными пределами. Интегралы от функций, имеющих разрыв.
Лекция 10. Применение определенного интеграла для геометрических и физических задач. Вычисление площадей плоских фигур, длин дуг плоских кривых,объёмов иплощадей поверхности вращения. Вычисление работы переменной силы, момента инерции.
Раздел 3. Дифференциальное и интегральное исчисление функций многих переменных.
Лекция 11. Понятие, предел и непрерывность функций многих переменных. Частные производные функций многих переменных.Понятие функции многих переменных и основные сведения. Предел и непрерывность функций двух переменных. Частные приращения функций многих переменных. Частные производные функций многих переменных. Геометрическое истолкование частных производных. Выражение частных производных через дифференциал. Полный дифференциал функции.
Лекция 12. Частные производные и дифференциалы высших порядков функций многих переменных. Исследование функций многих переменных. Применение дифференциала функции многих переменных. Приближенные вычисления с помощью полного дифференциала. Частные производные и дифференциалы функций многих переменных высших порядков. Касательная и нормаль к поверхности. Экстремумы функций многих переменных. Производная по направлению. Градиент.
Лекция 13. Кратные интегралы. Двойные интегралы. Геометрическое истолкование двойного интеграла. Свойства двойного интеграла. Вычисление двойного интеграла. Применение двойного интеграла.
Лекция 14. Тройной интеграл. Геометрические и физические приложения кратных интегралов.Тройной интеграл. Геометрические и физические приложения кратных интегралов.
Раздел 4. Дифференциальные уравнения.
Лекция 15. Однородные дифференциальные уравнения первого порядка.Основные определения. Свойства общего решения. Теорема Коши. Интегральные кривые. Особое решение. Дифференциальные уравнения первого порядка. Уравнения вида у’ = f(х). Уравнения с разделяющимися переменными. Однородные уравнения. Уравнения, приводящиеся к однородным.
Лекция 16. Линейные дифференциальные уравнения первого порядка. Уравнение Бернулли. Уравнения в полных дифференциалах. Уравнения Лагранжа и Клеро.Линейные уравнения. Линейные однородные дифференциальные уравнения. Линейные неоднородные дифференциальные уравнения. Метод Бернулли. Метод Лагранжа. Уравнение Бернулли. Уравнения в полных дифференциалах. Условие тотальности. Уравнения вида y = f(y’) и x = f(y’). Уравнения Лагранжа и Клеро.
Лекция 17. Дифференциальные уравнения высших порядков. Линейные однородные уравнения высших порядков. Уравнения, допускающие понижение порядка. Уравнения вида y(n) = f(x). Уравнения, не содержащие явно искомой функции и ее производных до порядка n-1 включительно. Уравнения, не содержащие явно независимой переменной. Линейные дифференциальные уравнения высших порядков. Линейные однородные дифференциальные уравнения с произвольными коэффициентами. Структура общего решения. Фундаментальна система решений. Определитель Вронского. Общее решение линейного однородного дифференциального уравнения второго порядка.
Лекция 18. Линейные неоднородные дифференциальные уравнения высших порядков. Линейные неоднородные дифференциальные уравнения с произвольными коэффициентами. Метод вариации произвольных постоянных. Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами. Уравнения с правой частью специального вида.
Лекция 19. Системы дифференциальных уравнений. Системы дифференциальных уравнений. Линейные системы. Нормальные системы линейных однородных дифференциальных уравнений с постоянными коэффициентами.

Раздел 1. Введение в математический анализ. Дифференциальное исчисление функций одной переменной.

Лекция 1. Функции одной переменной. Предел функции одной переменной.Понятие функции одной переменной. Способы задания функций. Классификация функций. Область определения функций. Графики функций. Предел функции. Основные теоремы о пределах. Первый и второй замечательный предел.

Числовая последовательность.

Определение. Если каждому натуральному числу n поставлено в соответствие число х_n, то говорят, что задана последовательность

x_1, х₂, …, х_n = {x_n}

Общий элементпоследовательности является функцией от n.

x_n = f(n)

Таким образом последовательность может рассматриваться как функция порядкового номера элемента.

Задать последовательность можно различными способами – главное, чтобы был указан способ получения любого члена последовательности.

Пример. {x_n} = {(-1)ⁿ} или {x_n} = -1; 1; -1; 1; …

{x_n} = {sinpn/2} или {x_n} = 1; 0; 1; 0; …

Для последовательностей можно определить следующие операции:

1) Умножение последовательности на число m: m{x_n} = {mx_n}, т.е. mx₁, mx₂, …

2) Сложение (вычитание) последовательностей: {x_n} ± {y_n} = {x_n ± y_n}.

3) Произведение последовательностей: {x_n}×{y_n} = {x_n×y_n}.

4) Частное последовательностей: 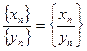при {y_n} ¹ 0.

Ограниченные и неограниченные последовательности.

Определение. Последовательность {x_n} называется ограниченной, если существует такое число М>0, что для любого n верно неравенство:

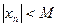
т.е. все члены последовательности принадлежат промежутку (-М; M).

Определение. Последовательность {x_n}называется ограниченной сверху, если для любого n существует такое число М, что

x_n £ M.

Определение. Последовательность {x_n}называется ограниченной снизу, если для любого n существует такое число М, что

x_n ³ M

Пример. {x_n} = n – ограничена снизу {1, 2, 3, … }.

Определение. Число а называется пределом последовательности {x_n}, если для любого положительного e>0 существует такой номер N, что для всех n > N выполняется условие:

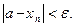
Это записывается: lim x_n = a.

В этом случае говорят, что последовательность {x_n}сходится к а при n®¥.

Свойство: Если отбросить какое- либо число членов последовательности, то получаются новые последовательности, при этом если сходится одна из них, то сходится и другая.

Пример. Доказать, что предел последовательности lim .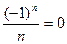

Пусть при n > N верно 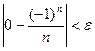, т.е. 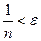. Это верно при 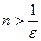, таким образом, если за N взять целую часть от 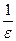, то утверждение, приведенное выше, выполняется.

Пример. Показать, что при n®¥ последовательность 3, 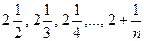имеет пределом число 2.

Итого: {x_n}= 2 + 1/n; 1/n = x_n – 2

Очевидно, что существует такое число n, что 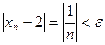, т.е. lim {x_n} = 2.

Теорема. Последовательность не может иметь более одного предела.

Доказательство. Предположим, что последовательность {x_n}имеет два предела a и b, не равные друг другу.

x_n ® a; x_n ® b; a ¹ b.

Тогда по определению существует такое число e >0, что

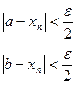
Запишем выражение: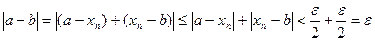

А т.к. e- любоечисло, то 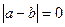, т.е. a = b. Теорема доказана.

Теорема. Если x_n ® a, то .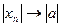

Доказательство. Из x_n ® a следует, что 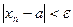. В то же время:

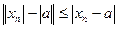, т.е. 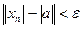, т.е. 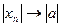. Теорема доказана.

Теорема. Если x_n ® a, то последовательность {x_n} ограничена.

Следует отметить, что обратное утверждение неверно, т.е. из ограниченности последовательности не следует ее сходимость.

Например, последовательность 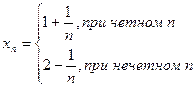не имеет предела, хотя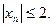

Монотонные последовательности.

Определение. 1) Если x_n+1 > x_n для всех n, то последовательность возрастающая.

2) Если x_n+1 ³ x_n для всех n, то последовательность неубывающая.

3) Если x_n+1 < x_n для всех n, то последовательность убывающая.

4)Если x_n+1 £ x_n для всех n, то последовательность невозрастающая

Все эти последовательности называются монотонными. Возрастающие и убывающие последовательности называются строго монотонными.

Пример. {x_n} = 1/n – убывающая и ограниченная

{x_n} = n – возрастающая и неограниченная.

Пример. Доказать, что последовательность {x_n}= 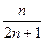монотонная возрастающая.

Найдем член последовательности {x_n+1}=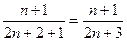

Найдем знак разности: {x_n}-{x_n+1}=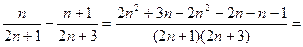

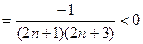, т.к. nÎN, то знаменатель положительный при любом n.

Таким образом, x_n+1 > x_n. Последовательность возрастающая, что и следовало доказать.

Пример. Выяснить является возрастающей или убывающей последовательность

{x_n} = .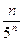

Найдем 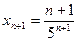. Найдем разность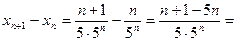

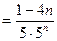, т.к. nÎN, то 1 – 4n <0, т.е. х_n+1 < x_n. Последовательность монотонно убывает.

Следует отметить, что монотонные последовательности ограничены по крайней мере с одной стороны.

Теорема. Монотонная ограниченная последовательность имеет предел.

Доказательство. Рассмотрим монотонную неубывающую последовательность

х₁ £ х₂ £ х₃ £ … £ х_n £ x_n+1 £ …

Эта последовательность ограничена сверху: x_n £ M, где М – некоторое число.

Т.к. любое, ограниченное сверху, числовое множество имеет четкую верхнюю грань, то для любого e>0 существует такое число N, что x_N > a - e, где а – некоторая верхняя грань множества.

Т.к. {x_n}- неубывающая последовательность, то при N > n а - e < x_N £ x_n,

x_n > a - e.

Отсюда a - e < x_n < a + e

-e < x_n – a < e или ôx_n - aô< e, т.е. lim x_n = a.

Для остальных монотонных последовательностей доказательство аналогично.

Теорема доказана.

Число е.

Рассмотрим последовательность {x_n} = .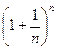

Если последовательность {x_n} монотонная и ограниченная, то она имеет конечный предел.

По формуле бинома Ньютона:

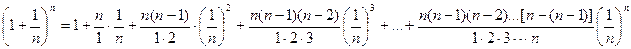или, что то же самое

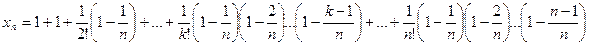
Покажем, что последовательность {x_n} – возрастающая. Действительно, запишем выражение x_n+1 и сравним его с выражением x_n:

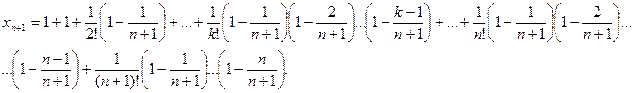Каждое слагаемое в выражении x_n+1 больше соответствующего значения x_n, и, кроме того, у x_n+1 добавляется еще одно положительное слагаемое. Таким образом, последовательность {x_n} возрастающая.

Докажем теперь, что при любом n ее члены не превосходят трех: x_n < 3.

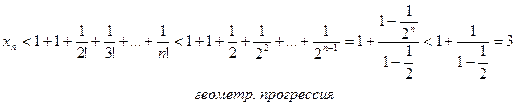
Итак, последовательность 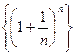- монотонно возрастающая и ограниченная сверху, т.е. имеет конечный предел. Этот предел принято обозначать буквой е.

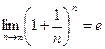
Из неравенства 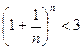следует, что е £ 3. Отбрасывая в равенстве для {x_n} все члены, начиная с четвертого, имеем:

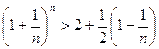
переходя к пределу, получаем

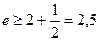
Таким образом, число е заключено между числами 2,5 и 3. Если взять большее количество членов ряда, то можно получить более точную оценку значения числа е.

Можно показать, что число е иррациональное и его значение равно 2,71828…

Аналогично можно показать, что 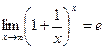, расширив требования к х до любого действительного числа:

Предположим: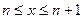

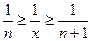
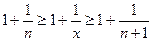
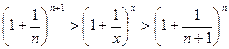
Найдем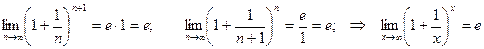

Число е является основанием натурального логарифма.

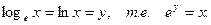
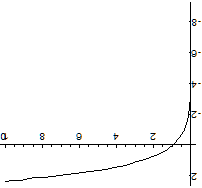
Выше представлен график функции y = lnx.

Связь натурального и десятичного логарифмов.

Пусть х = 10^у, тогда lnx = ln10^y , следовательно lnx = yln10

у = 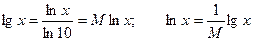, где М = 1/ln10 » 0,43429…- модуль перехода.

Предел функции в точке.

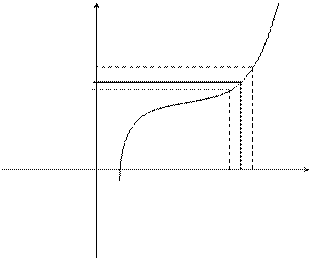y f(x)

A + e

A

A - e

0 a - D a a + D x

Пусть функция f(x) определена в некоторой окрестности точки х = а (т.е. в самой точке х = а функция может быть и не определена)

Определение. Число А называется пределом функции f(x) при х®а, если для любого e>0 существует такое число D>0, что для всех х таких, что

0 < ïx - aï < D

верно неравенство ïf(x) - Aï< e.

То же определение может быть записано в другом виде:

Если а - D < x < a + D, x ¹ a, то верно неравенство А - e < f(x) < A + e.

Запись предела функции в точке: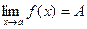

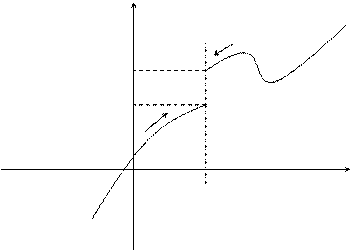
Определение. Если f(x) ® A₁ при х ® а только при x < a, то 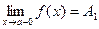- называется пределом функции f(x) в точке х = а слева, а если f(x) ® A₂ при х ® а только при x > a, то 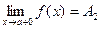называется пределом функции f(x) в точке х = а справа.

у

f(x)

А₂

А₁

0 a x

Приведенное выше определение относится к случаю, когда функция f(x) не определена в самой точке х = а, но определена в некоторой сколь угодно малой окрестности этой точки.

Пределы А₁ и А₂ называются также односторонними пределами функции f(x) в точке х = а. Также говорят, что А – конечный предел функции f(x).

Предел функции при стремлении аргумента к бесконечности.

Определение. Число А называется пределом функции f(x) при х®¥, если для любого числа e>0 существует такое число М>0, что для всех х, ïхï>M выполняется неравенство

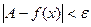
При этом предполагается, что функция f(x) определена в окрестности бесконечности.

Записывают: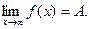

Графически можно представить:

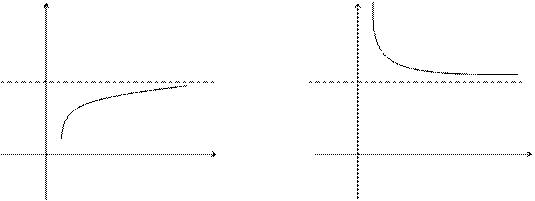y y

A A

0 0

x x

y y

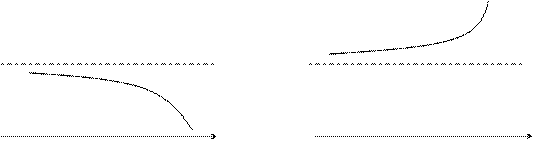A A

0 0

x x

Аналогично можно определить пределы 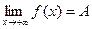для любого х>M и

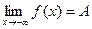для любого х<M.

Основные теоремы о пределах.

Теорема 1. 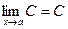, где С = const.

Следующие теоремы справедливы при предположении, что функции f(x) и g(x) имеют конечные пределы при х®а.

Теорема 2.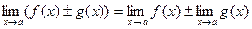

Доказательство этой теоремы будет приведено ниже.

Теорема 3.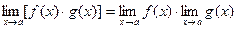

Следствие.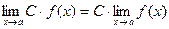

Теорема 4. 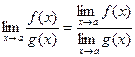при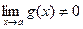

Теорема 5. Если f(x)>0 вблизи точки х = а и 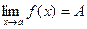, то А>0.

Аналогично определяется знак предела при f(x) < 0, f(x) ³ 0, f(x) £ 0.

Теорема 6. Если g(x) £ f(x) £ u(x) вблизи точки х = а и 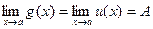, то и .

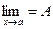Определение. Функция f(x) называется ограниченнойвблизи точки х = а, если существует такое число М>0, что ïf(x)ï<M вблизи точки х = а.

Теорема 7. Если функция f(x) имеет конечный предел при х®а, то она ограничена вблизи точки х = а.

Доказательство. Пусть 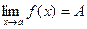, т.е. 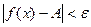, тогда

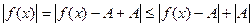или

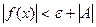, т.е.

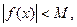где М = e + ïАï

Теорема доказана.

Лекция 2. Бесконечно малые и бесконечно большие функции. Непрерывность функции. Бесконечно малые и бесконечно большие функции. Сравнение бесконечно малых. Некоторые замечательные пределы. Понятие о непрерывности и точках разрыва функций. Свойства непрерывных функций. Классификация точек разрыва.

Бесконечно малые функции.

Определение. Функция f(x) называется бесконечно малой при х®а, где а может быть числом или одной из величин ¥, +¥ или -¥, если .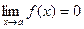

Бесконечно малой функция может быть только если указать к какому числу стремится аргумент х. При различных значениях а функция может быть бесконечно малой или нет.

Пример. Функция f(x) = xⁿ является бесконечно малой при х®0 и не является бесконечно малой при х®1, т.к. .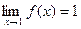

Теорема. Для того, чтобы функция f(x) при х®а имела предел, равный А, необходимо и достаточно, чтобы вблизи точки х = а выполнялось условие

f(x) = A + a(x),

где a(х) – бесконечно малая при х ® а (a(х)®0 при х ® а).

Свойства бесконечно малых функций:

1) Сумма фиксированного числа бесконечно малых функций при х®а тоже бесконечно малая функция при х®а.

2) Произведение фиксированного числа бесконечно малых функций при х®а тоже бесконечно малая функция при х®а.

3) Произведение бесконечно малой функции на функцию, ограниченную вблизи точки х = а является бесконечно малой функцией при х®а.

4) Частное от деления бесконечно малой функции на функцию, предел которой не равен нулю есть величина бесконечно малая.

Используя понятие бесконечно малых функций, приведем доказательство некоторых теорем о пределах, приведенных выше.

Доказательство теоремы 2. Представим f(x) = A + a(x), g(x) = B + b(x), где

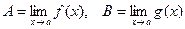, тогда

f(x) ± g(x) = (A + B) + a(x) + b(x)

A + B = const, a(х) + b(х) – бесконечно малая, значит

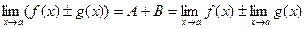
Теорема доказана.

Доказательство теоремы 3. Представим f(x) = A + a(x), g(x) = B + b(x), где

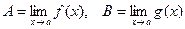, тогда

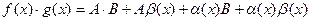
A×B = const, a(х) и b(х) – бесконечно малые, значит

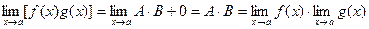
Теорема доказана.