Глава 2. и сдесь посмотри в оглавлении то что я тебе написал

2. Практическая часть

Рассмотрим примеры расчета параметров одноканальных и многоканальных СМО с отказами.

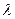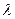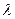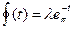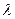Одно ка­нальная СМО содержит один канал (n = I), и на ее вход посту­пает пуассоновский поток заявок П_вх, интенсивность (среднее число событий в единицу времени) которого inП_вх = . Так как интенсивность входящего потока может изменяться во времени, то вместо записывают (t). Тогда время обслуживания каналом одной заявки Т_об распределено по показательному закону и за­писывается в виде: , где - интенсивность отказов.

Состояние СМО характеризуется простаиванием или занято­стью ее канала, т. е. двумя состояниями: s0 — канал свободен и простаивает, s1— канал занят. Переход системы из состояния s0 в состояние s1 осуществляется под воздействием входящего потока заявок П_вх, а из состояния s1, в состояние s0 систему переводит поток обслуживании П_об: если в данный момент времени система находится в некотором состоянии, то с наступлением первого по­сле данного момента времени СМО переходит в другое состояние. Плотности вероятностей перехода из состояния s0 в s1и обратно равны соответственно 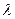и .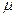

Для многоканальной СМО с отказами (n > 1) при тех же условиях состояния системы обозначим по числу занятых каналов (по числу заявок, находящихся в системе под обслуживанием, так как каждый канал в СМО либо свободен, либо обслуживав только одну заявку). Таким образом, подобная СМО может находиться в одном из следующих (n+1) состояний: s0 — все п каналов свободны; s1 — занят только один из каналов, остальные (n-1) каналов свободны; Si - заняты i каналов, (п—i) каналов свободны; Sn —заняты все п каналов.

Пользуясь общим правилом составления дифференциалы уравнений Колмогорова, можно составить системы дифференциальных уравнений:

а) например, для одноканальной СМО имеем:

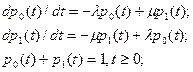
6) для многоканальной СМО соответствен имеем:

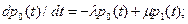
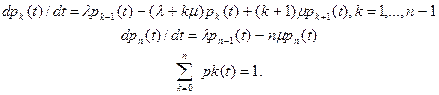
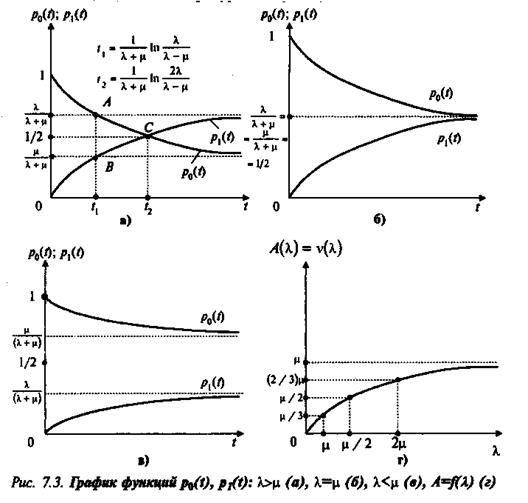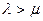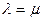Решив первую систему уравнений, можно найти значения p₀(t) и p₁(t) для одноканальной СМО и построить графики (рис.7.3, а-в) при трех случаях: 1) ; 2) ; 3) 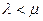. Можно также определить предельную пропускную способность СМО (рис. 7.3, г).

Теперь осуществим оценку эффективности деятельности субъектов рынка:

Пример 1. Пусть на телефонную линию филиала банка производительностью μ = 0,6 вызовов/мин и простейшим потоком обслуживания поступает простейший поток выозовов клиентов с интенсивностью λ = 0,3 вызовов/мин. Определить предельные значения относительной пропускной способности Q, абсолютной пропускной способности А и вероятности отказа P_отк телефонной линии, влияющие на итоговый доход филиала. Определить также среднее время обслуживания одного вызова, среднее время простоя канала и вероятность того, что канал свободен или занят.

Решение:Так как математической моделью телефонной линии является одноканальная СМО с отказами, характеризующаясями параметрами – интенсивностью входящего потока обслуживания inП_вх = 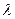= 0,3 и интенсивностью потока обслуживания inП_об = μ = 0,6, то по формуле:

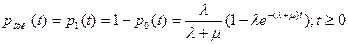
можно определить вероятность отказа так:

P_отк = 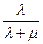= = 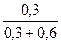0,333, или 33,3%, т.е. в установившемся предельном режиме из каждых 100 заявок в среднем 3 получат отказ.

Далее определим предельное значение относительной Q и абсолютной А пропускной способности СМО, используя формулу:

Q = 1 - P_отк = 1 – 0,333 = 0,667;

A= λ * Q =0,3*0,667=0,2.

Итак из расчета следует, что случайный характер поступления телефонных вызовов и случайный характер длительности разговора пораждают ситуацию, что абсолютная пропускная способность A= 0,2 разговора/мин в три раза меньше производительности телефонной линии μ = 0,6 вызова/мин (0,6:0,2 = 3).

Определим:

а) среднее время обслуживания (в мин) Т_об :

Т_об= 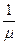= = 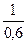1,66 мин;

б) среднее время простоя канала (в мин) Т_пр :

Т_пр= 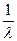= = 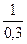3,33 мин;

в) вероятность того, что канал свободен :

P₀= 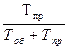= = 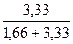0,2.

Или P0= 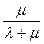= =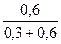0,666,

в) вероятность того, что канал занят P₁:

P₁= 1 – P₀ = λ/(λ+μ) = 0,334,

Или P₁= Т_об / (Т_об + Т_пр ) = 1,66 / (1,66+3,33) = 0,332.

Таким образом, вероятность того, что канал занят, ментше вероятности того, что канал свободен, т.е. P₁ < P₀, и этого следовало ожидать, так как интенсивность входящего потока λ = 0,3 меньше интенсивности производительности канала μ = 0,6.

Пример 2. Пусть филиал фирмы по ремонту радиоаппа­ратуры имеет n = 5опытных мастеров. В среднем в течение рабочего дня от населения поступает в ремонт l =10 радио­аппаратов. Общее число радиоаппаратов, находящихся в эксплуатации у населения, очень велико, и они независимо друг от друга в различное время выходят из строя. Поэтому есть все основания полагать, что поток заявок на ремонт ап­паратуры является случайным, пуассоновским. В свою оче­редь каждый аппарат в зависимости от характера неисправ­ности также требует различного случайного времени на ре­монт. Время на проведение ремонта зависит во многом от серьезности полученного повреждения, квалификации мас­тера и множества других причин. Пусть статистика показа­ла, что время ремонта подчиняется экспоненциальному за­кону; при этом в среднем в течение рабочего дня каждый из мастеров успевает отремонтировать m = 2,5 радиоаппарата. Требуется оценить работу филиала фирмы по ремонту радио­аппаратуры, рассчитав ряд основных характеристик данной СМО.

Решение: За единицу времени принимаем 1 рабочий день (7 часов).

1. Определим параметр

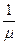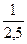a = l* = 10* = 4,

так как a < n, то очередь не может расти безгранично.

2. Вероятность того, что все мастера свободны от ремонта аппаратуры, равна :

P₀= 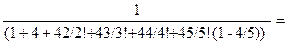0,013.

3. Вероятность того, что все мастера заняты ремонтом:

P_n= 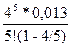= 0,554

Это означает, что 55,4% времени мастера полностью за­гружены работой.

4. Среднее время обслуживания (ремонта) одного аппарата:

Т_об = 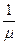= = 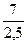2,8 ч/аппарат

(при условии семичасового рабочего дня).

5. В среднем время ожидания каждого неисправного аппа­рата начала ремонта равно:

t_ож= 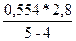= 1,55 ч.

6. Очень важной характеристикой является средняя длина очереди, которая определяет необходимое место для хранения аппаратуры, требующей ремонта:

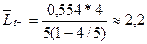
7. Определим среднее число мастеров, свободных от ра­боты:

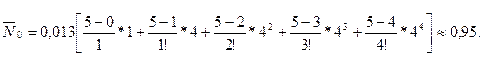
Таким образом, в среднем в течение рабочего дня ремонтом заняты четыре мастера из пяти.

ЗАКЛЮЧЕНИЕ

В настоящее время с развитием значения экономики в мире и увеличением числа изменяющихся характеристик для производителей требуются все более точные экономические рекомендации. Для ответа на вопросы, возникающие при осуществлении массового обслуживания, и создаются модели. Процесс их построения – моделирование.

Моделировать можно любой объект любой сложности, и именно моделирование дает порой те результаты, которые нельзя получить никаким другим способом.

Для начала моделирования необходимо:

1) изучить и выделить главные и второстепенные черты и свойства объекта;

2) расположить их друг за другом в определенной последовательности, указать их взаимосвязь;

3) поставить цель моделирования и определить показатели достижения цели (критерии);

4) разработать модели и средства для достижения цели и определить необходимые для этого ресурсы;

5) осуществить моделирование.

Моделирование СМО позволяет осуществить анализ экономических объектов СМО, спрогнозировать их развитие, подготовить обоснованные управленческие решения по совершенствованию деятельности. Модели позволяют изучить устройство конкретного объекта, апробируя различные варианты управления на модели объекта можно выбрать лучший вариант организации управленческой работы. Поэтому так важно на сегодняшний день уделить внимание разработке различных моделей системы мас­сового обслуживания, ведь с их помощью можно усовершенствовать способы функционирование множества предприятий, банков, кредитных учреждений, страховых организаций, налоговых ин­спекций, организаций сферы обслуживания (магазинов, больниц и др.), деятельность которых связана с многократной реализаци­ей исполнения каких-то однотипных задач и операций.

В первой части данной курсовой работы были достигнуты поставленные цели: была описана актуальности создания моделей СМО, раскрыты основные этапы моделирования и оптимизации систем, описаны структуры и их параметры эффективности функционирования, дана краткая классификация основных видов СМО.

Во второй части были приведены практические расчеты по использованию моделей СМО на примере трех предприятий:

была определена производительность, пропускная способность на телефонных линия филиала банка. Также среднее время обслуживания одного вызова, среднее время простоя канала и вероятность того, что канал свободен или занят. Были расчитаны значения, позволяющие принять оптимальное финансовое решение экономической организации филиала банка.

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ

1. Боровков А.А. Вероятные процессы в тероии массового обслуживания. – М.: Наука, 1972. с.20

2. Джонсон И.К. Экономические методы. – М.: ЮНИТИ, 1998. с.13-23.

3. Дрогобыцкий И.Н. Экономико-математическое моделирование. – М.: ЭКЗАМЕН, 2004. с.134.

4. Жданов С.А. Экономические модели и методы в управлении. – М.: Дело и сервис, 1998. с.25-77.

5. Замков О.О. Математические методы в экономике. – М.: Высшая школа, 1998. – 230с.

6. Петров А.А. Экономика. Модели. – М.: Наука, 1996. -251с.

7. Пинегин М.В. Математические методы и модели в экономике: Учебное пособие. – М.: ЭКЗАМЕН, 2002. с.123-131.

8. Федосеев В.В. Экономико-математические методы и прикладные модели. – М.: ЮНИТИ, 2002. с.314-326.

9. Черемных Ю.Н. Математические методы в экономике. – М.: ЮНИТИ, 1999.

с.10-15.

10. Чхартишвили А.Г., Шикин Е.В. Математические методы и модели в управлении. – М.: Экономика, 2000. с.34.

11. Шелобаев С.И. Математические методы и модели в экономике, финансах, бизнесе. – М.: ЮНИТИ, 2001. с.208-225.

12. Парамзин Н. Н. Методы и моделли в бизнесе. – М: ЮНИТИ, 2002. с.123-132.

И года поменяй в списке литературы книге не должно быть больше пяти лет, так что поменяй года, например 2009, или 2011 вот так вот, и еще кое что, в курсовой буквы все должны быть обычными, сдесь не должно быть курсива, или жирности, и текст должен быть TIMES NEW ROMAN 14.