Задания на выполнение лабораторной работы
Шифрование с помощью управляемых операций
Цель работы
Освоить порядок моделирования криптосистемы, основанной на шифрование с помощью управляемых операций, в программе Multisim 11.0.2.
Общие сведения
Программа Multisim может быть успешно использована для имитации работы криптографических систем. В предыдущей работе был рассмотрен шифр гаммирования. Основная идея шифра гаммирования заключается в замене символов открытого текста на числа и суммировании их с псевдослучайными числами, которые называются «гаммой». При этом состав гаммы известен только доверенным лицам на передающей и приёмной сторонах.
Известны методы взлома этого шифра. Скомпрометировать шифр можно в случаях нештатного использования гаммы (некачественный состав гаммы, малая длина или повторное использование одной и той же гаммы для шифрования разных сообщений).
Ещё одним уязвимым элементом в аддитивном шифре является логическая операция Исключающее ИЛИ, которая используется для зашифрования и расшифрования.
Известно интересное свойство этой логической операции:
.
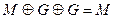Соотношение говорит о том, что наличие чётного числа одинаковых слагаемых, участвующих в операции Исключающее ИЛИ, уничтожает эти слагаемые. Таким образом, если определить период циклически повторяющейся гаммы и выполнить логическую операцию Исключающее ИЛИ над символами криптограммы с одинаковыми значениями гаммы (с одинаковыми фазами), то можно уничтожить гамму. В результате такого преобразования получаются данные, представляющие собой результат выполнения логической операции Исключающее ИЛИ над символами открытого текста:
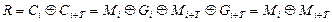
Это объясняется тем, что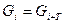 
, то есть элементы гаммы повторяются с периодом Т и поэтому они одинаковые. Если гамма дважды использована для шифрования двух разных текстов, то задача криптоанализа становится ещё проще: достаточно выполнить операцию Исключающее ИЛИ над двумя криптограммами. Известен пример неверного использования метода гаммирования в операционной системе Windows 95. Одна и та же гамма применялась несколько раз для шифрования данных в файлах PWL (эти файлы хранят логины и пароли).
Величину R можно назвать разностью открытых текстов (сообщений). Разность R может быть подвержена успешному криптоанализу путём учёта статистических закономерностей открытых текстов или использования известных из других источников их особенностей.
Таким образом, в аддитивном методе шифрования из-за симметричности (обратимости) логической операции Исключающее ИЛИ и нештатного использования гаммы существует возможность произвести криптоанализ и восстановить открытый текст даже без знания гаммы.
Повысить криптостойкость аддитивного шифра можно за счёт использования управляемых операций шифрования [3, 4]. Основная идея данной криптосистемы состоит в использовании в течение одного сеанса связи не одной, а нескольких различных шифрующих операций. В этой криптосистеме вместе с изменением значения гаммы варьируются операции преобразования, выполняемые над открытым текстом (на передаче) и над криптограммой (на приёме). Причём на передаче и приёме операции зашифрования и расшифрования должны синхронно чередоваться. Например, если на передаче осуществляется арифметическое сложение символа открытого текста с элементом гаммы, то на приёме нужно вычесть гамму из полученной криптограммы. Синхронизация выполняемых операций должна осуществляться под управлением гаммы, которая одновременно определяет и вид выполняемой операции, и сама участвует в этих операциях.
На рисунке показана структурная схема криптографической системы с управляемыми операциями шифрования.
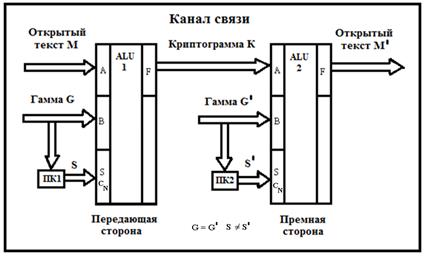
Имитация передающей и приёмной сторон криптосистемы осуществляется с помощью двух арифметико-логических устройств. Четыре разряда открытого текста M подаётся на вход А первого арифметико-логического устройства (АЛУ). Четырехбитная гамма G подаётся на входы В каждого АЛУ. Вид выполняемой операции на передающей стороне задаётся с помощью преобразователя кода ПК1. Управляющие сигналы S на приёмной стороне формируются с помощью преобразователя кода ПК2. Сигналы с выходов преобразователей кодов подаются на управляющие шины АЛУ и шину переноса из старшего разряда CN. Именно эти сигналы определяют вид выполняемых АЛУ операций.
Криптограмма K формируется на выходе F первого АЛУ. Расшифрование криптограммы происходит на приёмной стороне с помощью второго АЛУ. Выполняемые операции синхронно изменяются под управлением гаммы. Принятый открытый текст M` появляется на выходе F второго АЛУ.
В качестве шифрующих преобразований можно использовать различные логические и арифметические операции, а также математические функции и их комбинации [5]. Некоторые из них перечислены в таблице 2.1, в которой приняты такие обозначения:
M - открытый текст (сообщение); G - гамма; K - криптограмма;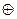 
- логическая операция Исключающее ИЛИ (неравнозначность); 
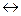- логическая операция равнозначность; «+» - арифметическая операция сложение; «–» - арифметическая операция вычитание; черта над переменными обозначает операцию инверсии.
Первые 10 операций в таблице 2.1 предполагают работу ЭВМ с целыми числами. Остальные операции предназначены для работы с вещественными числами.
Задачей преобразователей кодов ПК1 и ПК2 является синхронное изменение управляющих сигналов на передающей и приёмной сторонах. Естественно, что конструкции преобразователей кодов ПК1 и ПК2 должны быть разными, так как при одинаковых входных воздействиях (гамма G) преобразователи кодов должны формировать разные выходные (управляющие) сигналы S, S` и сигналы переносов CN.
Преобразователи кодов можно синтезировать различными способами: графически (с помощью карт Карно и диаграмм Вейча), аналитически (методы Квайна, Мак-Класки, неопределённых коэффициентов) и с помощью графических символов, интерпретирующих булевы функции.
Перечисленные способы синтеза комбинационных цифровых устройств трудоёмки и имеют ограничения на их использование при числе переменных более 5…6. При разработке модели данной криптосистемы преобразователи кодов целесообразно синтезировать с помощью блока Logic Converter (логический конвертор), который входит в систему моделирования радиоэлектронных устройств Multisim.
Таблица 2.1
| Операции на передающей стороне | Операции на приёмной стороне | |
| 1. | Неравнозначность 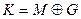 | Неравнозначность  |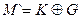
| 2. | Равнозначность 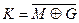 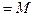 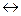 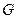| Равнозначность   |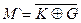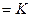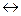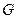
| 3. | Сложение 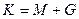 | Вычитание  |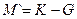
| 4. | Вычитание 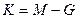 | Сложение  |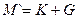
| 5. | Вычитание 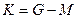 | Вычитание  |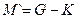
| 6. | Инверсия от суммы 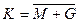 | Комбинированная разность  |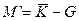
| 7. | Инверсия от разности 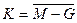 | Комбинированная сумма  |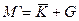
| 8. | Инверсия от разности 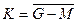 | Комбинированная разность  |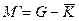
| 9. | Комбинированная сумма 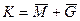 | Комбинированная разность  |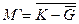
| 10. | Комбинированная разность 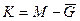 | Комбинированная сумма  |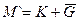
| 11. | Умножение 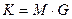 | Деление  |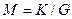
| 12. | Деление 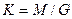 | Умножение  |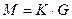
| 13. | Деление 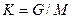 | Деление  |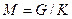
| 14. | Функциональные 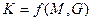 | Функциональные  |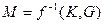
| 15. | Алгебраические 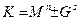 | Алгебраические  |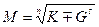
Логический конвертор позволяет создавать преобразователи кодов с числом аргументов n ≤ 8. Для получения логических выражений, описывающих работу ПК, достаточно в конвертор ввести таблицу истинности, которая описывает работу преобразователя кода. Полученные математические выражения затем можно использовать для построения принципиальной схемы ПК.
Рассмотрим подробнее порядок выбора логических и арифметических операций, которые можно использовать в криптосистеме.
Безусловно, для шифрования нужно использовать многократно проверенную на практике операцию Исключающее ИЛИ. Аналогичными положительными свойствами обладает операция “Равнозначность”, которая является инверсной по отношению к операции Исключающее ИЛИ.
В виду того, что логические операции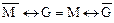 
эквивалентны операции неравнозначности 
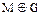, использовать все три операции при шифровании не имеет смысла, так как криптограммы при шифровании будут одинаковыми. Аналогично операции 
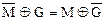сводятся к операции равнозначности 
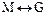. Таким образом, из рассмотренных шести операций следует использовать только две: равнозначность и неравнозначность.
Для арифметических операций в дополнительном коде справедливы соотношения:
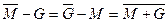
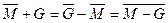
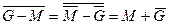
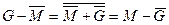
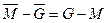
Использование операций, перечисленных в одной строке, даст одинаковые значения криптограммы при одинаковых значениях гаммы и открытого текста. Из четырнадцати указанных операций целесообразно оставить только шесть, например,
, 
, 
, 
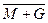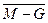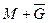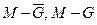и 
.
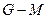Задания на выполнение лабораторной работы
3.1. Задание 1. Синтез преобразователя кода
Используя таблицу 3.1.1, разработать два преобразователя кода (по одному для передающей и приёмной стороны). Преобразователи кодов нужно синтезировать с помощью блока Logic Converter (логический конвертор).
Таблица 3.1.1
| Варианты | Значения гаммы G | |||
 |  |  |  | |
| 0,5,6,7 | 1,3,11 | 2,8,12,15 | 4,9,10,13,14 | |
| 2,3,7,11 | 8,12,14,15 | 0,1,5,9,13 | 4,6,10 | |
| 0,1,4,5 | 2,3,12,14,15 | 6,8,10 | 7,9,11,13 | |
| 0,13,14,15 | 4,6,8,10,12 | 1,3,5 | 2,7,9,11 | |
| 1,5,9,13 | 3,7,11,15 | 2,6,10,14 | 0,4,8,12 | |
| 0,5,10,15 | 3,6,9,12 | 4,8,7,11 | 1,2,13,14 | |
| 0,4,8,12 | 1,5,9,13 | 2,6,10,14 | 3,7,11,15 | |
| 2,6,10,14 | 0,4,8,12 | 3,7,11,15 | 1,5,9,13 | |
| 3,7,11,15 | 2,6,10,14 | 1,5,9,13 | 0,4,8,12 | |
| 4,5,8,9, | 2,3,12,13 | 0,1,6,7 | 10,11,14,15 | |
| 13,15,3,7 | 2,6,9,12 | 0,4,8,11 | 1,5,10,14 | |
| 2,3,6,7 | 10,11,14,15 | 4,5,8,9 | 0,1,12,13 | |
| 2,6,8,12 | 3,7,11,15 | 0,4,10,14 | 1,5,9,13 | |
| 5,7,10,13 | 4,6,12,15 | 0,2,8,11 | 1,3,9,14 | |
| 0,4,9,13 | 1,5,8,12 | 3,7,10,14 | 2,6,11,15 | |
| 3,7,8,12 | 0,4,10,14 | 2,6,11,15 | 1,5,9,13 | |
| 0,1,2,3 | 4,5,6,7 | 8,9,10,11 | 12,13,14,15 |
Таблица 3.1.1 показывает, какую операцию должна использовать криптосистема для указанного десятичного значения гаммы. Например, для варианта 17, если гамма равна 0, то выполняемая операция будет . Если значение гаммы равно 11, то операция на передающей стороне будет и т.д.