Правила составления сетевых графиков

1) Каждая работа должна быть заключена между двумя событиями. В сети не может быть работ, имеющих одинаковые коды.

2) В сети не должно быть событий, из которых не выходит ни одной работы, если только это событие не является для данного графика завершающим. Соответственно, в сети не должно быть события, в которое не входит ни одной работы, если только это событие не является исходным.

3) В сетевом графике не должно быть замкнутых контуров.

Сроки выполнение работ и резервы времени

Ранним сроком t_p(j) совершения события j называется минимальное время, к которому необходимо завершить все работы, предшествующие этому событию:

t_p(j) = .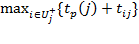

Поздним сроком t_п(j) завершения события i называется максимально допустимый срок наступления этого события, не требующий увеличения времени на осуществление всего проекта:

t_п(j) = .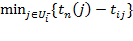

Полный резерв R_П(i, j) – максимальное количество времени, на которое можно перенести начало работ или увеличить ее продолжительность без изменения общего срока проекта t_кр:

R_П(i, j) = t_п(j) – t_p(i) – t_ij.

Свободный резерв R_С(i, j) – запас времени, на который можно перенести начало работы или увеличить ее продолжительность (при условии, что работа начата в свой ранний срок) без изменения раннего срока начала последующих работ:

R_С(i, j) = t_р(j) – t_p(i) – t_ij.

Если R_C <0, то резерв заменяется нулем.

Всегда выполняется неравенство R_П ≥R_C.

Для работ. Принадлежащих критическому пути резерв времени равен нулю.

Резерв времени R(i) – количество времени, на которое может задержаться свершение события i без изменения общего срока выполнения работ t_кр:

R(i) = t_п(i) – t_p(i).

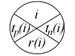
Кроме выше перечисленных показателей работ, определяют ранние и поздние сроки начала и окончания работ. Эти показатели непосредственно связаны и ранними и поздними сроками совершения событий.

Ранний срок начала работы t_рн(i, j)= t_р(i).

Ранний срок окончания работы t_ро(i, j)= t_р(i)+ t_ij.

Поздний срок начала работы t_пн(i, j)= t_п(j) – t_ij.

Поздний срок окончания работы t_по(i, j)= t_п(j).

Пример

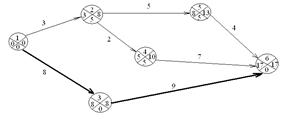
Определить для представленной сети сроки событий и резервы времени.

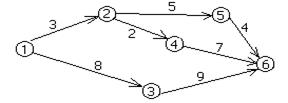
Определим t_кр, для этого рассчитаем продолжительность путей от события 1 до события 6.

П1: 1 – 2 – 5 – 6, t₁=t(П1)=3+5+4=12;

П2: 1 – 2 – 4 – 6, t₂=t(П2)=3+2+7=12;

П3: 1 – 3 – 6, t₃=t(П3)=8+9=17.

t_кр = max{12, 12, 17}=17.

Определим ранний сроки свершения событий.

t_p(1) = 0,

t_p(2) = t_p(1) +t_1,2 = 0+3=3,

t_p(3) = t_p(1) +t_1,3 = 0+8=8,

t_p(4) = t_p(2) +t_2,4 =3+2=5,

t_p(5) = t_p(2) +t_2,5 =3+5=8,

t_p(6) = t_кр =17.

Теперь рассчитаем поздний срок совершения событий

t_п(1) = 0,

t_п (2) = min{t_п (4) – t_2,4 ; t_п (5) – t_2,5 }= min{10 – 2; 13 – 5} = min{8;8}=8,

t_п (3) = t_п (6) – t_3,6 =17 – 9 =8,

t_п (4) = t_п (6) – t_4,6 =17 – 7 = 10,

t_п (5) = t_п (6) – t_5,6 =17 – 4 =13,

t_п (6) = t_кр =17.

Определим резервы событий:

R(1)= t_n(1) – t_p(1) =0 – 0 =0,

R(2)= t_n(2) – t_p(2) =8 – 3 =5,

R(3)= t_n(3) – t_p(3) =8 – 8 =0,

R(4)= t_n(4) – t_p(4) =10 – 5 =5,

R(5)= t_n(5) – t_p(5) =13 – 8 =5,

R(6)= t_n(6) – t_p(6) =17 – 17 =0.

Для определения характеристик работ, воспользуемся таблицей, в которой для удобства проведем вычисления.

	(1, 2)	(1, 3)	(2, 4)	(2, 5)	(3, 6)	(4, 6)	(5, 6)
tрн(i, j)
tро(i, j)
tпн(i, j)
tпо(i, j)
RП(i, j)
RС(i, j)

Сети Петри

Сети Петри — математический аппарат для моделирования динамических дискретных систем. Сеть Петри представляет собой ориентированный граф, состоящий из вершин двух типов — позиций и переходов, соединённых между собой дугами, вершины одного типа не могут быть соединены непосредственно. В позициях могут размещаться метки (маркеры), способные перемещаться по сети.

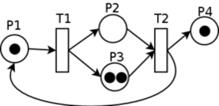
Белыми кружками обозначены позиции, полосками — переходы, чёрными кружками — метки.

Рис. 8. ?? Пример сети Петри.

Событием называют срабатывание перехода, при котором метки из входных позиций этого перехода перемещаются в выходные позиции. События происходят мгновенно, либо разновременно, при выполнении некоторых условий.

Виды сетей Петри

• временная сеть Петри — переходы обладают весом, определяющим продолжительность срабатывания (задержку);
• стохастическая сеть Петри — задержки являются случайными величинами;
• функциональная сеть Петри — задержки определяются как функции некоторых аргументов, например, количества меток в каких-либо позициях, состояния некоторых переходов;
• цветная сеть Петри — метки могут быть различных типов, обозначаемых цветами, тип метки может быть использован как аргумент в функциональных сетях;
• ингибиторная сеть Петри — возможны ингибиторные дуги, запрещающие срабатывания перехода, если во входной позиции, связанной с переходом ингибиторной дугой, находится метка;
• иерархическая сеть — содержит не мгновенные переходы, в которые вложены другие, возможно, также иерархические, сети. Срабатывание такого перехода характеризует выполнение полного жизненного цикла вложенной сети.

Анализ сетей Петри

Основными свойствами сети Петри являются:

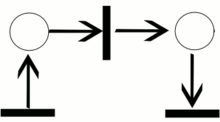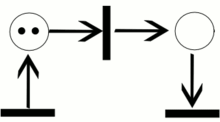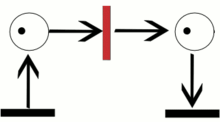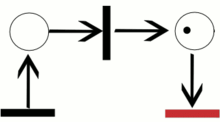
Пример траектории в сети Петри.

• ограниченность — число меток в любой позиции сети не может превысить некоторого значения K;
• безопасность — частный случай ограниченности, K=1;
• сохраняемость — постоянство загрузки ресурсов, т.е. 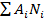постоянна, где N_i — число маркеров в i-той позиции, A_i — весовой коэффициент;
• достижимость — возможность перехода сети из одного заданного состояния (характеризуемого распределением меток) в другое;
• живость — возможность срабатывания любого перехода при функционировании моделируемого объекта.

В основе исследования перечисленных свойств лежит анализ достижимости.