Вставка одного элемента в массив
При вставке одного элемента в массив необходимо сначала освободить место для вставляемого элемента, т.е. “раздвинуть” элементы, а затем вставить новый элемент в массив и увеличить длину массива на 1.
Пример
Дан массив – 3 2 0 6 – 8 12 5 0. После первого числа 0 вставить сумму всех элементов массива.
Программный код
Sub PR21()
Dim x(20) As Integer
Dim n As Integer, i As Integer
Dim i0 As Integer ‘ порядковый номер числа
Dim a As Integer
n = Val(InputBox("Введите n"))
s = 0
For i = 1 To n
x(i) = Cells(1, i) ‘ ввод массива и
s = s + x(i) ‘ вычисление суммы элементов
Next i
‘ поиск порядкового номера первого числа 0
For i = 1 To n
If x(i) = 0 Then
i0 = i
Exit For ‘ выход из цикла
End If
Next i
‘ раздвигаем элементы
For i = n + 1 To i0 + 1 Step –1
x(i) = x(i – 1)
Next i
n = n + 1
x(i0 + 1) = s ‘ вставка элемента
Cells(3, 1) = "полученный массив"
For i = 1 To n
Cells(4, i) = x(i)
Next i
End Sub
При раздвижке элементов массив приобретет следующий вид:
– 3 2 0 0 6 – 8 12 5 0.
После вставки получим массив – 3 2 0 14 6 – 8 12 5 0.
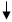
s
Вставка группы элементов в массив
Пример
В одномерный массив перед каждым числом 0 вставить сумму всех элементов массива.
Фрагмент программы, в котором происходит вставка элементов, выглядит следующим образом:
i = 1
While i <= n
If x(i) = 0 Then
For j = n + 1 To i + 1 Step –1
x(j) = x(j – 1)
Next j
x(i) = s
n = n + 1
i = i + 2
Else
i = i + 1
End If
Wend
Двумерные массивы
Двумерные массивы представляют набор однотипных элементов, расположенных в несколько строк и столбцов, например, двумерный массив из целых чисел выглядит следующим образом:
4 –3 2 4 5
6 3 2 4 0
7 1 2 6 0
12 24 25 8 4
0 4 5 8 3
Каждый элемент двумерного массива обозначается при помощи имени и индексов, заключенных в круглые скобки, например, A(i, j), X(4, 3), P(2×i, j+1), первый индекс – номер строки, второй – номер столбца.
Двумерный массив, называемый также матрицей, описывается при помощи оператора Dim.
Dim A(10, 10) As Тип ‘ нумерация с нуля
Dim A(1 To 10, 1 To 10) As Тип ‘ нумерация с единицы
Матрица, у которой количество строк равно количеству столбцов, называется квадратной матрицей.
Ввод двумерного массива
1. Считывание массива с рабочего листа Excel.
For i = 1 To N
For j = 1 To M
A(i, j) = Cells(i, j)
Next j
Next i
‘ N – количество строк массива, M – количество столбцов массива.
2. Формирование массива на рабочем листе Excel при помощи счетчика случайных чисел, а затем считывание массива с рабочего листа.
Randomize
For i = 1 To N
For j = 1 To M
Cells(i, j) = Int(Rnd * 100 – 50)
A(i, j) = Cells(i, j)
Next j
Next i
Вывод двумерного массива
Вывод двумерного массива на рабочий лист Excel выглядит следующим образом:
For i = 1 To N
For j = 1 To M
Cells(i, j) = A(i, j)
Next j
Next i
Формирование матрицы
При формировании квадратной матрицы будем пользоваться следующими инструкциями. Общий вид квадратной матрицы, например размерности 4´4, выглядит следующим образом:
| А11 | А12 | А13 | А14 |
| А21 | А22 | А23 | А24 |
| А31 | А32 | А33 | А34 |
| А41 | А42 | А43 | А44 |
В квадратной матрице выделяются главная и побочная диагонали. Условия нахождения элемента на главной или побочной диагонали показаны на рис. 7.
Относительно каждой диагонали элемент матрицы может находиться выше или ниже диагонали. Условия нахождения элемента в каждой из частей матрицы показаны на рис. 8.
I, J – номера строки и столбца, в которых находится элемент матрицы.
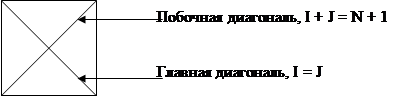 |
Рис. 7. Главная и побочная диагонали
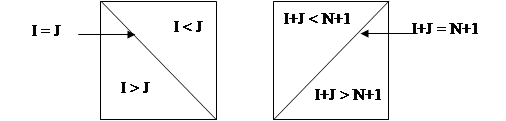 |
Рис. 8. Условия нахождения элемента выше или ниже диагонали
Относительно обеих диагоналей элемент матрицы может находиться в одной из четвертей. Условия нахождения элемента в каждой из них показаны на рис. 9.
 | |||
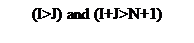 |
Рис. 9. Нахождение элемента в одной из четвертей
Пример 1
Сформировать матрицу X(N, N) вида
На побочной диагонали матрицы стоят 5, на главной диагонали стоят 4, в I четверти – 0, во II четверти – 2, в III четверти – 3, в IV четверти – 1.
Программный код
Option Explicit
Sub PR22()
Dim a(10, 10) As Integer
Dim N As Integer
Dim i As Integer
Dim j As Integer
N = Val(InputBox("Введите N"))
Range(Cells(1, 1), Cells(100, 100)).Select ‘ выделяет диапазон ячеек
Selection.Clear ‘ очищает выделенный диапазон ячеек
Cells(1, 1).Select ‘ снимает выделение
For i = 1 To N
For j = 1 To N
If i + j = N + 1 Then a(i, j) = 5
If i = j Then a(i, j) = 4
If i < j And i + j < N + 1 Then a(i, j) = 0
If i < j And i + j > N + 1 Then a(i, j) = 2
If i > j And i + j > N + 1 Then a(i, j) = 3
If i > j And i + j < N + 1 Then a(i, j) = 1
Next j
Next i
Cells(1, 1) = "Полученная матрица"
For i = 1 To N
For j = 1 To N
Cells(i + 1, j) = a(i, j)
Next j
Next i
End Sub
Пример 2
Сформировать матрицу X(N, N) вида
| … | N | ||||
| … | |||||
| … | |||||
| . | . | . | . | … | . |
| … | |||||
| … | N |
Описание и вывод матрицы будут как в предыдущем примере, здесь и далее будем рассматривать только фрагмент программы, в котором формируется матрица.
For i = 1 To N
For j = 1 To N
X(i, j) = 0
If i = j Then X(i, j) = i
If i + j = N + 1 Then X(i, j) = N + 1 – i
Next j
Next i
Пример 3
Сформировать матрицу Y(N, N) вида
| … | |||||
| … | |||||
| … | |||||
| . | . | . | . | … | . |
| … | |||||
| … | |||||
| … |
For i = 1 To N
For j = 1 To N
If i = 1 Or i = N Or j = 1 Or j = N Then Y(i, j) = 1 Else Y(i, j) = 0
Next j
Next i
Пример 4
Сформировать матрицу Z(N, N) вида
| … | ||||||
| … | ||||||
| … | ||||||
| … | ||||||
| . | . | . | . | . | . | . |
| … | ||||||
| … | N |
For i = 1 To N
For j = 1 To N
If i >= j Then Z(i, j) = j Else Z(i, j) = 0
Next j
Next i
Пример 5
Сформировать матрицу Q(N, N) вида
| … | ||||
| … | ||||
| … | ||||
| . | . | . | . | … |
| … |
For i = 1 To N
For j = 1 To N
If (i +j) mod 2 = 0 Then Q(i, j) = 1 Else Q(i, j) = 2
Next j
Next i
