Сравнение оптимизации в частотной области с оптимизацией методом подбора коэффициентов
МОСКОВСКИЙ АВИАЦИОННЫЙ ИНСТИТУТ
(национальный исследовательский университет)
«МАИ»
Учебная дисциплина
«Основы электротехники и радиоэлектроники»
КУРСОВАЯ РАБОТА
Тема: Матричный анализ линейных схем
Выполнил:
Студент Никитин Р.А.
Группа: № 4О-208Сцк
Серпухов 2015
ГЛАВА 4 ОПТИМИЗАЦИЯ СХЕМ
Пример 4.8
Матрицу частных производных из примера 4.4 можно получить, вводя источники тока, как это изображено на фиг. 4.15, Из схемы фиг. 4.15 имеем
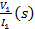 =
= 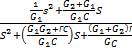 , (4.123)
, (4.123)
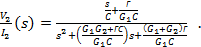 (4.124)
(4.124)
Матрица частных производных строится из числителей выражений (4.123) и (4.124)
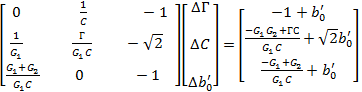 ,
,
(4.125)
(4.125)
что аналогично (4.86) при условии 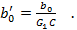 Здесь, как и в
Здесь, как и в
примере 4.4, выбор b'0 не оказывает влияния на итерацию. Поэтому можно положить b'0 = 1, а 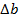 '0 вообще опустить. При этом fo (соответствующая коэффициенту при старшем члене) всегда будет равняться нулю. Коэффициенты считаются найденными, когда |fi|< ε, i = 1, 2, . . n— 1, и на этом итерации заканчиваются. В более общем случае, когда положение некоторых полюсов безразлично, можно после каждой итерации вычислять
'0 вообще опустить. При этом fo (соответствующая коэффициенту при старшем члене) всегда будет равняться нулю. Коэффициенты считаются найденными, когда |fi|< ε, i = 1, 2, . . n— 1, и на этом итерации заканчиваются. В более общем случае, когда положение некоторых полюсов безразлично, можно после каждой итерации вычислять 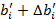 [уравнение (4.125)] и затем нормировать эту величину делением на
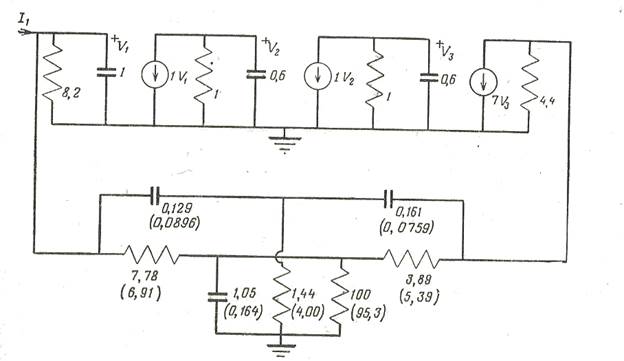
[уравнение (4.125)] и затем нормировать эту величину делением на 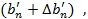 т. е.
т. е.
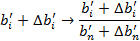
И в этом случае итерации заканчиваются, когда |fi|<ε.
При м е р 4.9 .
Активный RС-фильтр, изображенный на фиг. 4.16, в исходном состоянии неустойчив (главный полюс в точке s = 0,0169 ± j0,566). Следует изменить элементы схемы таким образом, чтобы главный полюс переместился в точку s = —0,05 + j1. При вычислении импедансов для всех подбираемых элементов была использована программа анализа с помощью уравнений состояния. На фиг. 4.15 в скобках указаны окончательные значения параметров элементов, полученные за шесть итераций, которые заняли 4 сек машинного времени на машине IBM 360-67.
Фиг. 4.16, Схема активного фильтра. В скобках указаны значения параметров элементов после корректировки главных полюсов.
Сравнение оптимизации в частотной области с оптимизацией методом подбора коэффициентов
Напомним, что при проектировании узкополосных схем для получения точных частотных характеристик нужно иметь весьма точные значения коэффициентов схемной функции. Частные производные от этих коэффициентов нужно знать еще точнее, так как они используются в ходе итераций при обращении матриц. Очевидно, наиболее точно (но зато с большими затратами времени) частные производные получаются при помощи аналитических (символических) методов. Методами уравнений состояния производные вычисляются гораздо быстрее (но менее точно). Сейчас принято считать на основании опытных данных, что символические методы предпочтительнее при вычислениях с обычной длиной слова (8 значащих цифр), а численные (матричные) методы — при вычислениях с удвоенной точностью. И в том, и в другом случае сложность схемы обычно ограничена 25 элементами и 15 узлами, так как большая часть машинного времени уходит на получение коэффициентов схемной функции и их производных, которые перевычисляются при каждой итерации путем обращения матрицы, [s I— А]. (Альтернатива состоит в обращении рациональной матрицы методом, аналогичным изложенному в гл. 3.)
Итак, может сложиться впечатление, что оптимизация в частотной области обладает неоспоримыми вычислительными преимуществами, так как при помощи методов гл. 3 перевычислить частные производные совсем несложно. Вернемся, однако, к задаче об оптимизации фильтра с потерями, сформулированной в начале данной главы. Как показано в работе [28], коэффициенты знаменателя функции передачи по напряжению V2(s)/V1 (s) можно с точностью до константы сделать равными коэффициентам знаменателя функции передачи идеального фильтра (без потерь), сохраняя заданное соотношение между элементами LC (аналогично тому, как это делается в примере 4.5). Таким образом, удалось подобрать коэффициенты со значительно более высокой точностью, благодаря чему характеристика фильтра оказалась почти идеальной. Превосходство этой характеристики над характеристикой схемы, полученной при оптимизации в частотной области, проявляется в том, что: 1) подбором коэффициентов удалось устранить проблему локального минимума, тогда как полученная при оптимизации в частотной области характеристика, изображенная на фиг. 4.2, представляет собой как раз локальный минимум для функции ошибки F(х, ω); 2) если даже иногда удается другими методами подобрать F(х, ω), которая не дает локальных минимумов, все же метод подбора коэффициентов требует от проектировщика значительно меньше труда и изобретательности при выборе различных функций ошибок.
Резюмируя сказанное здесь и в разд. 4.8.1, можно утверждать, что метод подбора коэффициентов является наиболее подходящим для некоторых классов хорошо обусловленных численных задач, если в распоряжении проектировщика имеются удобные способы вычисления частных производных (см. [33]).
4.10. Минимизация чувствительности [19]
Лишние степени свободы, возникающие при превышении числа варьируемых параметров элементов над минимально необходимым числом таких параметров, можно использовать для оптимизации самих критериев. Очень полезным критерием является чувствительность характеристик схемы к изменениям параметров элементов. Следуя рассуждениям предыдущего раздела, будем осуществлять оптимизацию в s-плоскости, так что речь пойдет о чувствительности собственных частот схемы.
Изменение положения полюса определяется как
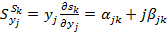 (4-127)
(4-127)
где Sk находится из
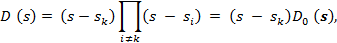
(4.128)
причем Sk — простой корень. Таким образом, согласно (4.127), чувствительность есть изменение Sk, поделенное на относительное изменение уj. Поэтому чувствительность является комплексным числом. Как уже говорилось ранее, полиномы, входящие в схемную функцию, являются линейными функциями от каждого элемента, т. е. мы можем написать следующее выражение:
D(s) = D1(s) + yjD2(s). (4.129)
Теперь можно показать (предоставляем это читателю в качестве упражнения), что
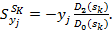 (4.130)
(4.130)
Если схема обладает одним главным корнем, тогда можно минимизировать αik, βik или ( 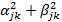 ). Минимизация αik делает схему более устойчивой, минимизация βik повышает стабильность частоты, минимизация
). Минимизация αik делает схему более устойчивой, минимизация βik повышает стабильность частоты, минимизация 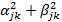 обеспечивает общее уменьшение чувствительности схемы. Мы будем заниматься минимизацией
обеспечивает общее уменьшение чувствительности схемы. Мы будем заниматься минимизацией 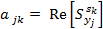 .
.
Пусть необходимо получить заданное снижение чувствительности, т. е. 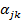 = а0. Положим
= а0. Положим
fi = αjk — а0 (4.131)
тогда fi — 0 является решением поставленной задачи. Или же уравнение (4.131) можно присоединить к уравнениям метода подбора коэффициентов при условии, что частные производные вычисляются так, как это изложено ниже.
Так как в общем случае D(s) может иметь как главные, так и неглавные корни, то, как и в подразд. 4.8.3, можно написать
D(s) = (b0 + bls+ ... + bmsm) (a0 + a1s+ ... + ansn), (4.132)
D (s) = В(s) A(s), (4.133)
причем корни полинома A(s)—главные. Пусть sk — главный корень, тогда
D(s) = B(s)A0(s)(s-sk). (4.134)
Обозначим
D0(s) = B(s) A0(s). (4.135)
Знаменателем 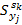 является
является
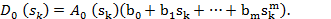 (4.136)
(4.136)
Дальнейшие выкладки основываются на том, что исходная и конечная схемы имеют одни и те же главные полюса и, значит, один и тот же полином A0(sk). Поэтому можно считать A0(sk) константой, a D0(Sk) — функцией только bi.
Анализируя числитель полинома D2(sk), мы видим, что его коэффициенты тоже линейно зависят от значений параметров элементов схемы.
Теперь нетрудно вычислить частные производные 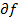 i/
i/ 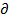 ym и
ym и 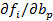
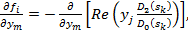 (4.137)
(4.137)
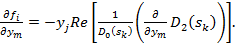 (4.138)
(4.138)
Так как D2(Sk) тоже линейно зависит от ут, то получение частных производных не составляет особого труда.
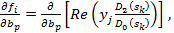 (4.139)
(4.139)
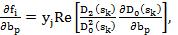 (4.140)
(4.140)
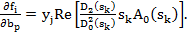 (4.141)
(4.141)
Пример 4.10
Желательно уменьшить на 20% чувствительность для схемы фиг. 4.13:
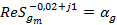
Элементы C1,R2, Г — переменные; их начальные значения 0,8012; 49,7 и 1,0 соответственно (см. табл. 4.12).
Имея в виду, что полином в знаменателе содержит корень
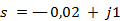 , его можно записать таким образом:
, его можно записать таким образом:
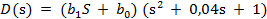 , (4.143)
, (4.143)
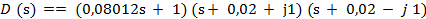 (4.144)
(4.144)
или же
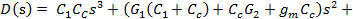
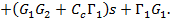 (4.145)
(4.145)
Отсюда
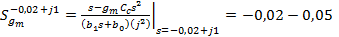 (4.146)
(4.146)
В этом случае, поскольку ни gm, ни Сс не являются переменными, частные производные равны
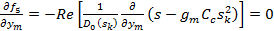 (4.147)
(4.147)
Далее
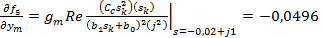 (4.148)
(4.148)
И
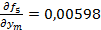
Последующие итерации отражены в табл. 4.14.
Таблица 4.14
Последовательные итерации в примере 4.10
| Номер итерации | С1 | L1 | R2 |
| 0,8012 | 1,0000 | 49,70 | |
| 1,3090 | 0,6747 | 22,63 | |
| 1,2389 | 0,6961 | 26,30 | |
| 1,2377 | 0,6961 | 26,61 |
Пример 4.11
Схема активного полосового фильтра на фиг. 4.17 отличается тем свойством, что все проводимости имеют одинаковый температурный коэффициент, а все β имеют в три раза больший температурный коэффициент. Желательно сделать главный корень нечувствительным к изменениям всех β и проводимостей.
30.6
(54)

Фиг. 4.17. Схема активного фильтра. В скобках указаны значения параметров элементов после минимизации чувствительности.
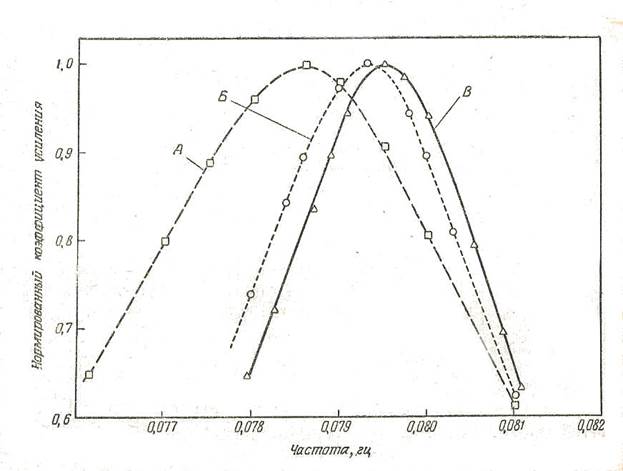
Фиг. 4.18. Влияние минимизации чувствительности на частотную характеристику.
А — исходная схема (Q = 19,7); Б — схема с минимизированной чувствительностью после изменения проводимостей на 5% и β на 15% по сравнению с расчетными (Q == 28,4); В—схема с минимизированной чувствительностью при расчетных значениях элементов (Q — 30,6).
Легко показать, что в любой схеме сумма чувствительностей всех проводимостей для одного и того же корня равна самому корню. В данной схеме, имеющей главный корень s1 = —0,0081 + j0,5,
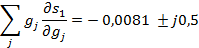
Так как β изменяются с температурой в три раза быстрее проводимостей, то, учитывая противоположный знак этого изменения,
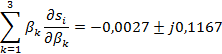
Но так как 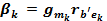 ,
,
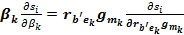 ,
,
То
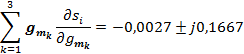
На фиг. 4.17 указаны начальные и конечные (в скобках) значения параметров элементов. Вычисления заняли 2,5 мин. Графики, показывающие влияние одновременного изменения всех β и проводимостей, приведены на фиг. 4.18.
4.11. Метод непрерывного преобразования схем с сохранением эквивалентности [18,31]
В качестве заключения в данной главе рассмотрим один метод машинного проектирования схем, который, хотя и выглядит несколько академически по сравнению с мощными итерационными методами, изложенными ранее, все же может служить одним из примеров нетрадиционного подхода к решению классических задач с помощью современных вычислительных машин.
Пусть заданы: схемная функция T(s), которая должна быть синтезирована, и начальная реализация схемы N1. Требуется найти другую схему, эквивалентную N1, но с другими значениями параметров элементов или, может быть, имеющую структуру, отличающуюся от N1. Например, если схемная функция имеет вид
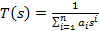 (4.150)
(4.150)
тогда любая схема N2 реализующая функцию
 , (4,151)
, (4,151)
эквивалентна N1 с точностью до коэффициента усиления.
Один способ получения класса схем, содержащего N2, состоит в том, что коэффициенты а1 берутся из множества решений
дифференциального уравнения
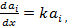
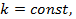
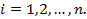 (4.152)
(4.152)
Так как
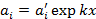 (4.153)
(4.153)
то очевидно, что b0= exp kx. Здесь без потери общности можно положить k=1.
Значение уравнения (4.152) состоит в том, что любое аi можно записать как функцию адмиттансов элементов yj. Раскрывая уравнение (4.152), имеем
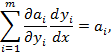
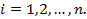 (4.154)
(4.154)
Или можно написать матричное дифференциальное уравнение

При m = n, если уравнения независимы, с помощью обращения матрицы можно найти единственные решений для 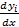 .
.
П р и м е р 4.12
Фильтр, изображенный на фиг. 4.11, имеет функцию передачи по напряжению (с учетом сопротивления источника R1)
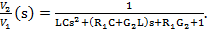
Необходимо при G2=const и увеличении Ri сохранить функцию передачи неизменной.
Уравнения (4.152) записываются в данном случае в таком виде:
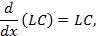
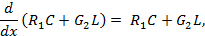
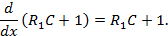
Или в матричной записи 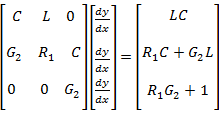
Переходя к обычной форме записи, получаем
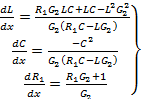 (4.155)
(4.155)
Эти уравнения можно проинтегрировать методами численного анализа, взяв исходные значения параметров элементов схемы фильтра в качестве начальных.
Указанную методику вряд ли можно рекомендовать для больших схем, поскольку при численном интегрировании нужно брать малый шаг, чтобы поддерживать точность элементов в разумных границах. Поэтому почти всегда предпочитают использовать метод подбора коэффициентов. Тем не менее идея введения параметров сама по себе является полезной.
Заключение
Укажем некоторые направления современных исследований в области машинного проектирования радиоэлектронных схем:
1. Методы чебышевской аппроксимации частотных и временных характеристик [30, 32]. Предложенные до настоящего времени методы подобного типа являются либо узко специализированными, либо имеют сравнительно малые области сходимости или склонны приводить к локальному минимуму. Однако достоинства методов чебышевской аппроксимации вполне заслуживают дальнейших исследований в этом направлении.
2. Оптимизация (нелинейных) переключательных и импульсных схем [30].
3. Автоматическая трансформация и модификация топологии схемы: исключение, замена и введение новых элементов [13, 30, 31]. Автоматический синтез топологии схемы из схем холостого хода и схем короткого замыкания.
ЗАДАЧИ
4.1. Показать, что в методе наискорейшего спуска направление, определенное на i-й итерации, ортогонально направлению, определенному на
(i— 1) -й итерации, если âi-1 вычислено точно.
4.2. Флегчер и Поуэлл показывают, что их метод обеспечивает сходимость к А-1 в том случае, когда минимизируемая функция квадратичная, доказывая, что вектор 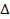 xj является линейно независимым от предыдущих (j — 1) векторов. Почему из этого следует сходимость к А-1?
xj является линейно независимым от предыдущих (j — 1) векторов. Почему из этого следует сходимость к А-1?
4.3. Разложение в ряд Тейлора с остаточным членом для функции n переменных имеет следующий вид:
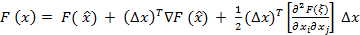 ,
,
где 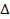 х = x —
х = x — 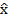 ,
, 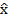 — точка глобального минимума, £ лежит на отрезке х +/Ах (О^/s^l). Доказать, что если
— точка глобального минимума, £ лежит на отрезке х +/Ах (О^/s^l). Доказать, что если 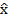 является локальным минимумом, тогда гессиан не может быть положительно определенной матрицей на всем отрезке.
является локальным минимумом, тогда гессиан не может быть положительно определенной матрицей на всем отрезке.
4.4. Плохую обусловленность в задачах, где функция F имеет эллипсоподобные линии постоянного уровня (как на фиг. 4.4а), можно устранить, реализуя итерации не по хi, а по log хi . Показать на примере, как это делается.
4.5. Дополнить математическое условие унимодальности так, чтобы оно годилось для n-мерного пространства. Изобразите чашеобразный участок поверхности, который удовлетворяет условию унимодальности, но не является выпуклым.
4.6. Можно показать, что в методе поиска с помощью чисел Фибоначчи
начальные интервалы стремятся к пределу 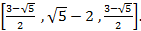 Если выбрать в качестве начальных эти интервалы, то какими выражениями описываются длины интервалов при последующих итерациях? Почему этот метод менее эффективен, чем изложенный в подразд. 4.4.3?
Если выбрать в качестве начальных эти интервалы, то какими выражениями описываются длины интервалов при последующих итерациях? Почему этот метод менее эффективен, чем изложенный в подразд. 4.4.3?
4.7. Показать, что в методе подбора коэффициентов должно выполняться следующее обязательное условие: число варьируемых элементов должно быть Не меньще числа полюсов, которые хотят сохранить на том же месте.
4,8, Высокочастотная малосигнальная модель транзистора, изображенная на схеме 34.1, содержит элементы у, которые зависят от тока смещения эмиттера. В частности, 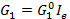 ,
, 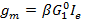 (ток Iе в миллиамперах). Мы хотим компенсировать изменения, вызываемые током эмиттера, путем варьирования параметра одного или нескольких элементов. Если требуется сохранить два главных полюса, то сколько элементов нужно сделать варьируемыми, чтобы матрица частных производных была квадратной? Найти эту матрицу.
(ток Iе в миллиамперах). Мы хотим компенсировать изменения, вызываемые током эмиттера, путем варьирования параметра одного или нескольких элементов. Если требуется сохранить два главных полюса, то сколько элементов нужно сделать варьируемыми, чтобы матрица частных производных была квадратной? Найти эту матрицу.
4.9. Пусть ограничение на элемент G выражается неравенством 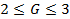 . Подобрать а1 и
. Подобрать а1 и 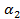 в выражении
в выражении
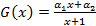 так, чтобы неравенство для G выполнялось в случае х, изменяющейся в интервале [0,
так, чтобы неравенство для G выполнялось в случае х, изменяющейся в интервале [0, 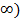 . Найти схему, реализующую G, в которой каждая проводимость
. Найти схему, реализующую G, в которой каждая проводимость

Фиг. 34.1. Полосовой усилитель.
либо постоянна, либо имеет вид Gix. Обратите внимание на то, что для 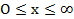 итеративная схема, приведенная в подразд. 4.8.4.2, гарантирует, что G будет ограниченной величиной.
итеративная схема, приведенная в подразд. 4.8.4.2, гарантирует, что G будет ограниченной величиной.
4.10 Минимизировать функцию F(x) при ограничениях 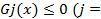
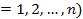 с помощью метода, изложенного в подразд. 4.7.2, положив
с помощью метода, изложенного в подразд. 4.7.2, положив
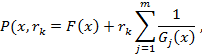
где rk<rk-1 . Пусть 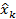 обозначает ту величину
обозначает ту величину 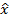 , при которой P(x,rk) достигает минимума. Показать, что F(
, при которой P(x,rk) достигает минимума. Показать, что F( 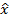 k+1) <F(
k+1) <F( 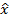 k) и
k) и 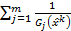 . (Не обязательно требовать, чтобы функции F и Gj были выпуклой и вогнутой соответственно.) Если итерации начинаются вблизи от границы Gj =0, а минимум достигается далеко от границы, то каким образом сумма
. (Не обязательно требовать, чтобы функции F и Gj были выпуклой и вогнутой соответственно.) Если итерации начинаются вблизи от границы Gj =0, а минимум достигается далеко от границы, то каким образом сумма 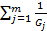 может убывать, как это требуется?
может убывать, как это требуется?
4.11.В этой главе рассмотрен метод вычисления производных от коэффициентов полинома 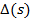 который в общем случае является знаменателем некоторой схемной функции. Попытайтесь развить аналогичный метод вычислений производных от коэффициентов полинома в числителе, исходя из методики измерений параметров n-полюсника, аналогичной методике, отраженной на фиг. 4.15 (Указание: используйте методы вычисления частных производных в частотной и временной областях, изложенные в гл. 3.) Разработайте способ рекурсивного вычисления производных от коэффициентов при помощи методов пространства состояний. (Указание: примените метод разбиений или методы теории n-полюсников, рассмотренные в гл. 1 применительно к анализу нелинейных цепей.) Следует отдельно рассматривать случаи резистивных и реактивных элементов.
который в общем случае является знаменателем некоторой схемной функции. Попытайтесь развить аналогичный метод вычислений производных от коэффициентов полинома в числителе, исходя из методики измерений параметров n-полюсника, аналогичной методике, отраженной на фиг. 4.15 (Указание: используйте методы вычисления частных производных в частотной и временной областях, изложенные в гл. 3.) Разработайте способ рекурсивного вычисления производных от коэффициентов при помощи методов пространства состояний. (Указание: примените метод разбиений или методы теории n-полюсников, рассмотренные в гл. 1 применительно к анализу нелинейных цепей.) Следует отдельно рассматривать случаи резистивных и реактивных элементов.
4.12. Метод подбора коэффициентов имеет тесную связь с методом подбора корней [28]. Пусть 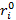 — заданный (комплексный) корень; положим
— заданный (комплексный) корень; положим
Fi=ri - 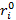 (i=1, 2, …, m), тогда fi = 0 является искомым решением. Пусть n-степень рассматриваемого полинома. Найти связь между двумя методами: а) при m =n; б) при т<n (случай главных и неглавных корней). Коэффициенты, естественно, подбираются с точностью до постоянного множителя. Используйте материал данной главы по чувствительности корней.
(i=1, 2, …, m), тогда fi = 0 является искомым решением. Пусть n-степень рассматриваемого полинома. Найти связь между двумя методами: а) при m =n; б) при т<n (случай главных и неглавных корней). Коэффициенты, естественно, подбираются с точностью до постоянного множителя. Используйте материал данной главы по чувствительности корней.
ЛИТЕРАТУРА
1. Kuhn Н. W., Now-Linear Programming, Proc. Second Symposium on Mathematical Statistics and Probability, Univ. of California Press, Berkeley, 1951.
2. Linvi 11 J. G., Network Alignment Techniques, Proc. IRE, 41, 290—293 (February 1953).
3. Aaron M. R., The Use of Least Squares in System Design, IRE Trans, on Circuit Theory, CT3, 224—231 (December 1956).
4. Arrow K. J-, Hurwicz L., Uzawa H., Studies in Linear and Non- Linear Programming, Stanford Univ. Press, 1958.
5. D e n n i s J. В., Mathematical Programming and Electrical Networks, MIT Press, 1959; см. русский перевод: Деннис Дж. Б., Математическое программирование и электрические цепи, ИЛ, 1961.
6. Desoer С. A., Mitra S. К., Design of Lossy Ladder Filters by Digital Computer, IRE Trans, on Circuit Theory, CT8, 192—201 (September 1961).
7. Carrol, C. W., The Created Response Surface Technique for Optimizing Non-Linear Constrained Systems, Opns. Res., 9, 169—184 (1961).
8. Spang H. A., A Review of Minimization Techniques for Non-Linear Functions, SI AM Review, 4, 343—365 (1962).
9. Fletcher R., Powell M. J. D., A Rapidly Convergent Descent Method for Minimization, The British Computer Journal, 6, 163—168 (1963).
10. Rice J. R., The Approximation of Functions^ Addison — Wesley, 1963.
11. Werner H., Rationale Tschebyscheff — Approximation, Eigenwerttheo- rie, und Differenzenrechnung, Arch. Rat. Mech. Anal., 13, 330—337 (1963).
12. Fiacco A. V., M с С о r m i с k G. P., The Sequential Unconstrained Technique for Non-Linear Programming, Algorithm II, Optimum Gradients by Fibronacci Search, Research Analysis Corp. Report RAC-TP-123, June 1964.
13. Calahan D. A., Computer Solution of the Network Realization Problem, Proc. Second Allerton Conference, Univ. of Illinois, pp. 175—200, 1964.
14. Fiacco A. W., McCormick G. P., The Sequential Unconstrained Minimization for Nonlinear Programming, A Primal — Dual Method, Management Service, 10, 360—366 (1964).
15. Murata Т., The Use of Adaptive Constrained Descent in Systems Design, IEEE International Conv. Rec., Part 1, 296—306 (1964).
16. P о w e l l M. J. D., An Efficient Method for Finding the Minimum of a Function of Several Variables Without Calculating Derivatives, The British Computer Journal, 155—162 (1964).
17. Fiacco А. V., McCormick G. P., The Sequential Unconstrained Minimization Techniques for Convex Programming with Equality Constraints, Research Analysis Corp. Report RAC-TP-155 (April 1965).
18*. Calahan D. A., Computer Design of Linear Frequency Selective Networks, Proc. IEEE, 53, 1701—1706 (November 1965).
19. Calahan D. A., A Numerical Algorithm for the Minimization of Sensitivity, Proc. Third Allerton Conference, 394—406 (1965).
20. P о w e l l M. J. D., A Method for Minimizing a Sum of Squares of Nonlinear Functions Without Calculating Derivatives, British Computer Journal, 7, 303—307 (1965).
21. Scheibe P. O., Huber E. A., The Application of Carroll's Optimization Technique to Network Synthesis, Third Allerton Conference, 182—191 (1965).
22.Temes G. C., Bingham J. A. C., Iterative Chebyshev Approximation Technique for Equalizer Synthesis, Proc. Third Allerton Conference, Univ. of Illinois, 773—785 (1965).
23.War en A. D., L a s d о n L. S., Practical Filter Design Using Mathematical Optimization, Proc. Third Allerton Conference, Univ. of Illinois, 677— 689 (1965).
24. L a s d о n L. S., Waren A. D., Optimal Design of Filters with Bounded, Lossy Elements, Trans. IEEE, CT13, 175—187 (June 1966).
25.Athanassopoulos I. A., S с h о e f f 1 e r J. D., Waren A. D., Time-Domain Synthesis by Nonlinear Programming, Fourth Allerton Conference, 766—775 (1966).
26.W i l d e D. J., В e i g h 11 e r C. S., Foundations of Optimization, Prentice- Hall, 1967.
27.Lovi A., Vogl T. P., Recent Advances in Optimization Techniques, Wiley, 1966.
28*. Temes G. С., С a 1 a h a n D. A., Computer Aided Network Optimization— The State of the Art. Proc. IEEE (November 1967).
29. Gaash A. A., P e p p e r R. S., P e d e r s о n D. O., Design of Integrable Desinsitized Frequency Selective Amplifiers, /. of Solid State Cir. № 1, 29— 34 (December 1966).
30*. См. другие статьи в журнале Proc. IEEE, November, 1967.
31.Schoeffler J. D., The Synthesis of Minimum Sensitivity Networks, Trans IEEE, CT11, 271—288 (June 1964).
32.Temes G. C., Gyi M., Design of Filters with Arbitrary Passband and Chebyshev Stopband Attenuation, IEEE Conv. Record, 15, 5, 2—12 (March 1967).
33. H a m 111 о n A. W., The Use of Computers in the Design of Color Television Receivers. Trans. IEEE on Broadcast and Television Receivers 34—39 (July 1967).
ГЛАВА 5
