Усреднение модели измерений

МОСКОВСКИЙ АВИАЦИОННЫЙ ИНСТИТУТ

(государственный технический университет)

Факультет

Прикладной математики и физики

КУРСОВАЯ РАБОТА

«анализ и планирование эксперимента»

Выполнил: студент группы 08-504

Никольский Г. Л.

Вариант 9

Преподаватель: Горяинов А. В.

Москва

Постановка задачи

Пусть плоская траектория точки характеризуется следующей моделью.

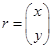- координаты точки,

,

,

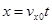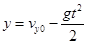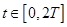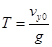, – время подъёма на максимальную высоту, 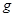– ускорение свободного падения. На интервале 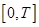могут производиться измерения дельности 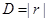от начальной точки полёта до движущейся точки в моменты 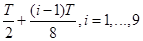. Предполагается, что номинальное значение модуля начального импульса равно 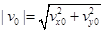= 1000 м/с, значение угла наклона равно 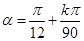, где 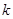– номер студента по списку.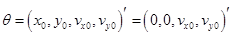

В качестве контролируемых параметров принимаются координаты 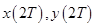, которые могут отличаться от номинальных в результате ошибок исполнения начального импульса 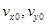. Для контролируемых параметров решить задачу L-оптимального планирования эксперимента с точностью до 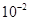(или выше), т.е. найти оптимальные значения моментов измерений 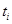и соответствующие доли от общего числа измерений 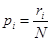. Критерий минимизации – сумма дисперсий оценок контролируемых параметров.

, .

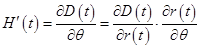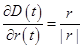Теоретическая часть

Усреднение модели измерений

Пусть θ вектор неизвестных параметров системы, и при i = 1,...,n проводится r_i измерений y_ij, j = 1,..., ri функции H’Q. Обычно считают, что измерения y_ij при заданном i проводятся в заданный момент времени t_i (возможен и другой параметр привязки всех измерений у^ при заданном i, например дальность полета при движении точки по траекто­рии). Тогда можно измерения в этот момент считать сеансом измерения. Например, космические измерения проводятся сеансами, соответствующи­ми небольшим интервалам времени, в течение которого есть радиовиди­мость космического объекта. Эти интервалы часто можно при планирова­нии космического эксперимента заменить отдельными моментами t_i.

Предполагается, что ошибки измерений являются некоррелированными между собой случайными величинами с нулевыми математическими ожи­даниями и единичными дисперсиями. Согласно теореме Гаусса-Маркова, в классе линейных нсмещенных алгоритмов оценивания минимальную дис­персию оценки любого параметра дает МНК, соответствующий весовой матрице W = I. Учитывая это, осредним модель оценивания.

ЛеммаПри использовании МНК исходную модель измерений

y_ij = Н’Q + ε_ij, j = 1,..., п; i = 1,..., n

можно заменить усредненной моделью

y_i = H'_i Q+ ε_i; i = 1,...,n,

есть средние арифметические указанных выше ri измеренных значений yij ошибок εij.

При этом εi есть некоррелированные между собой случайные величины, математические ожидания которых равны нулю/

Постановка задачи

Пусть задано общее число измерений N. Вместо чисел ri будем использовать вектор p с координатами r_i/N/ Далее будем, как это обычно делают, пренебрегать целочисленностью ri и считать, что р непрерывный план эксперимента, т.е. любой вектор из симплекса

Пусть b_j – заданные векторы, l_j - контролируемые параметры. Этот оцениватель дает несмещенные оценки параметров b'-Q тогда и только тогда, когда он удовлетворяет условиям несмещенности, т.е. bj есть линейная комбинация тех векторов, для которых pi > 0. Да­лее будем обозначать P_n множество тех p из Σ_n, для которых выполняются условия несмещенности (3.6) (для некоторых Φij).

Для каждого p ∈ P_n рассмотрим наилучшие линейные несмещенные оценки, для которых оцениватель определяется из условия минимальных дисперсий при линейном несмещенном оценивании:

Задача оптимального планирования эксперимента состоит в нахождении плана р G n, доставляющего нижнюю грань заданному критерию опти­мальности L(p):

L = inf{L(p):p∈P_n}.

Мы будем рассматривать два критерия оптимальности, предполагая да­лее, что оценки (3.5) являются наилучшими нелинейными несмещенными. Первый критерий есть критерий L-оптимальности. Второй критерий

L(p)² = Nmax{Dlˆ1,...,Dlˆ_s}

будем называть MVs-критерием (при s = m и lj = θj, j = 1,..., m крите­рий (3.10) называют просто MV-критерием). В зависимости от критерия (3.9) или (3.10) задачу (3.8) будем соответственно называть L-задачей или MV_s-задачей. При решении задачи (3.8) будем предполагать, что

(3.11) rапк{Н’,...,Н'_п) =m

(т.е. ранг составной матрицы максимален), что равносильно допущению о возможности линейного несмещенного оценивания всех компонент вектора в в случае использования всех n групп измерений.

В дальнейшем будем считать указанные замены при суммировании и оптимизации произведенными.

3.3. Скалярная задача планирования эксперимента и алгоритм

Ее решения

При s = 1L-задача (а также MVs-задача) сводится к минимизации дис­персии 1Л, где l = l1 и называется C -задачей планирования эксперимента. Проведем далее минимизацию дисперсии по pi, пренебрегая тем, что ri должно быть целым. Это оправдано при достаточно большом N. Получим, используя множители Лагранжа, что оптимальный план измерений есть

Замечание 3.4. Указанная оптимизация по п здесь проведена не совсем строго (так же как и в основополагающей работе [24]). Действительно, мы проводили оптимизацию по pi только при условии p1 + .. .+pn = 1. Однако, не при всех таких pi может выполняться условие несмещенности, т.е. может быть получена оценка параметра l. (В связи с этим условие несмещенности также называют условием оцениваемости.) Поэтому множество допусти­мых pi может быть несколько меньше, а искомый минимум не меньше. Однако, ввиду того, что получившееся решение приводит к допустимым оценкам, это решение является верным.

Оптимизация величины D0, полученной при оптимальных ri, по оцени-вателю x приводит к задаче линейного программирования

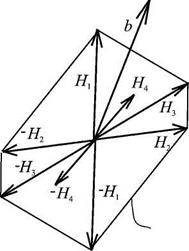conv {Я,, Н2,Щ,Щ

Рис. 2. Построение выпуклой оболочки множеств Hi ^пр^и решении задачи (3.16)

Сформулированную задачу можно интерпретировать следующим обра­зом: следует разложить вектор b по векторам ±Hi с коэффициентами yi > 0 и минимизировать сумму коэффициентов. Эта задача представляет собой задачу линейного программирования, геометрический способ ее решения (в двумерном случае) обсуждался в предыдущей главе. У этой задачи су­ществует оптимальное решение, содержащее не более m отличных от нуля коэффициентов, т.е. вектор b лежит внутри многогранного угла, образо­ванного некоторыми m векторами ±Hi (базисом), причем гиперплоскость, проведенная через их концы, отсекает от вектора b наибольшую часть по сравнению с другими комбинациями из m векторов. Легко заметить, что указанная гиперплоскость, проходящая через концы векторов опти­мального базиса, принадлежит выпуклой оболочке всех 2n векторов ±Hi, i=1,... ,n (см. рис.2).

Таким образом мы делаем важный вывод. При решении скалярной зада­чи планирования эксперимента следует выбрать оптимальные m измерений и найти оцениватель для усредненной модели.