Математическое дополнение

1. Вывод распределения Гаусса.

Возьмём в качестве исходного, биномиальное распределение

(1)

Прологарифмируем + (2)

Значение m= ,при котором P достигает максимума найдём из условия:

=0 или = 0 = (3)

При этом для каждого факториала воспользуемся приближением Дифференцируя (2): C учётом, что p+q=1, найдем значение m= :

Для получения компактной записи функции распределения, разложим lnP в окрестности в ряд Тейлора. Свойства этого разложения таковы, что члены ряда быстро убывают и можно ограничиться первыми членами разложения.

](m- (4)

Так как первая производная от lnP равна нулю при m= (3), то ограничим ряд только вторым членом:

Вторую производную легко вычислить из (3): =

В точке Вторая производная

Разложение (4) примет вид:

(5)

Величина (постоянная) :

Последний интеграл сводится к табличному :

Полагая , и , получим распределение Гаусса:

.

2. Статистический смысл энтропии (полный вывод).

Пусть изолированная термодинамическая система находится в состоянии с энергией . Это состояние равновероятно реализуется способами. Разобьём условно систему на две подсистемы и , таких, что гамильтонианы систем связаны соотношением: Положим далее, что внешние силовые поля отсутствуют и элементы подсистем не взаимодействуют между собой, но могут обмениваться энергией. Для изолированной системы выполняется закон сохранения энергии: сумма энергий подсистем равна энергии сложной системы: . Пусть число доступных состояний и подсистем А и А₁ соответствует случаям, когда их энергии лежат , соответственно, в интервалах Е,

Е+ δЕ и Е₁, Е₁+δЕ_1. Найдём вероятность того, что из общего числа состояний системы А_{0 ,} часть соответствует состоянию подсистемы А с энергией Е. По определению вероятности:

(11)

то есть вероятность пропорциональна числу доступных состояний.

В тоже время каждое из состояний подсистемы А с энергией Е можно комбинировать с любым доступным состоянием подсистемы с энергией . Тогда полное число доступных состояний системы , в которых энергия подсистемы равна , будет выражаться произведением:

(12)

( так как произведение вероятностей пропорционально произведению числа доступных состояний). С учётом (12) соотношение (11) примет вид (13)

Воспользуемся каноническим распределением Гиббса и связью вероятности с плотностью распределения вероятности

(14)

где - плотность распределения вероятности.

(15)

Интегрируя (14), с учётом (15) и получим искомую вероятность:

(16)

Здесь D - некоторый параметр, который переходит в постоянную величину в равновесном состоянии системы . Найдём условия перехода системы и её подсистем в равновесное состояние.

Равновесное состояние системы характеризуется максимальной вероятностью или максимальным числом доступных состояний. Для нахождения условий равновесного перехода исследуем на максимум:

Заметим, что производная от логарифма вероятности по энергии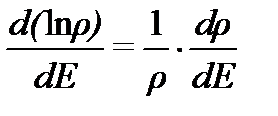

равна нулю в тех же точках, что и производная от вероятности.

Так как D не зависит от энергии, то (17)

Равенство (17) показывает, что равновесное состояние системы наступит тогда и только тогда, когда параметры Т и подсистем А и станут равными соответствующему параметру системы . Этот параметр - абсолютная температура.

Поскольку абсолютная температура всегда только положительная величина, то в процессе перехода в равновесное состояние должно выполняется условие .

Введём некоторую функцию, которая могла бы указывать направление передачи энергии в процессе перехода системы в равновесное состояние. Прологарифмируем (13) и приравняем нулю производную по энергии.

(18)

При выводе (18) учтено, что Выделим из соотношений (18) равенство:

Преобразуем последнее выражение к виду: (19)

Для анализируемой термодинамической системы левая часть равна нулю в тех же точках, что и производная от вероятности.

Так как D не зависит от энергии, то (17)

Равенство (17) показывает, что равновесное состояние системы наступит тогда и только тогда, когда параметры Т и подсистем А и станут равными соответствующему параметру системы . Этот параметр - абсолютная температура.

Поскольку абсолютная температура всегда только положительная величина, то в процессе перехода в равновесное состояние должно выполняется условие .

Введём некоторую функцию, которая могла бы указывать направление передачи энергии в процессе перехода системы в равновесное состояние. Прологарифмируем (13) и приравняем нулю производную по энергии. (18)

При выводе (18) учтено, что Выделим из соотношений (18) равенство:

.

Преобразуем последнее выражение к виду: (19)

Для анализируемой термодинамической системы левая часть представляет собой разность приведённых теплот, которыми обмениваются подсистемы А и . Правая часть должна быть равна по определениям классической молекулярной физики разности дифференциалов энтропий этих подсистем. Следовательно: Это и есть статистическое определение энтропии термодинамической системы, введённое М.Планком.

Теперь (19) можно переписать в виде:

Полагая, что по прежнему Т₁ >Т, в правой части тогда dS > dS_{1 ,} то есть подсистема А получает тепло, а подсистема А₁ его отдаёт. В изолированной системе поток тепловой энергии направлен от подсистемы с большей температурой к подсистеме с более низкой температурой. Исходя из аддитивности энтропии, можно утверждать, что энтропия изолированной термодинамической системы не убывает.

(20) Неравенство (20) представляет собой второе начало термодинамики в энтропийной формулировке.

Программа курса физики.. КНиИТ, 1 курс ,2 семестр.

МЕХАНИКА

Раздел 1. Введение.

Математический аппарат физики. Векторы и операции с ними.

Раздел 2. Кинематика.

Материальная точка. Системы отсчета. Траектория. Перемещение и путь. Скорость и ускорение. Тангенциальное и нормальное ускорения. Классификация движения по ускорению. Кинематика прямолинейного и вращательного движений точки. Кинематика колебательного и волнового движений. Примеры, практические задачи.

Движение твёрдого тела. Степени свободы. Поступательное и вращательное движение твёрдого тела. Теорема Эйлера о произвольном движение твёрдого тела.

Раздел 3. Законы динамики.

Основная задача динамики. Первый закон Ньютона. Инерциальные системы отсчета. Взаимодействие тел. Сила. Масса и импульс тела. Второй закон Ньютона, и его особенности. Третий закон Ньютона и границы его применимости.

Твёрдое тело. Момент импульса, момент силы, момент инерции. Уравнение моментов - дифференциальное уравнение движения твёрдого тела. Уравнения динамики колебательного и волнового движений (волновое уравнение). Примеры, практические задачи.

Раздел 4. Законы сохранения.

Закон сохранения импульса и его особенности. Закон сохранения момента импульса. Примеры: распад нейтрона, движение планет солнечной системы, гироскоп.

Работа сил. Потенциальная и кинетическая энергия. Работа и энергия вращения Закон сохранения механической энергии. Примеры, практические задачи.

Раздел 5. Гравитационное поле.

Закон всемирного тяготения. Гравитационное поле. Гравитационная энергия. Гравитационный радиус. «Чёрные дыры» Движение в поле тяготения Земли. Космические скорости.

Раздел 6. Движение в неинерциальных системах отсчёта.

Силы инерции в общем случае. Поступательные и центробежные силы инерции. Сила Кориолиса. Проявления сил инерции в движениях на Земле.

Раздел 7. Элементы теории относительности. Примеры

МОЛЕКУЛЯРНАЯ СТАТИСТИЧЕСКАЯ ФИЗИКА.

Раздел 1. Введение.

Предмет и методы молекулярной физики и термодинамики. Развитие представлений о строении вещества. Молекулярно-тепловое движение. Межмолекулярные силы. Равновесное состояние термодинамической системы. Температура.

Раздел 2. Динамическая теория идеального газа.

2.1. Давление и средняя энергия молекул газа. Основное уравнение молекулярно-кинетической теории идеального газа. Изопроцессы.

2.2. Столкновения молекул. Средняя длина свободного пробега. Явления переноса в газах: диффузия, внутреннее трение, теплопроводность.

Раздел 3. Основы статистического описания термодинамических систем. .

3.1.Основные понятия. Микро- и макропараметры состояния. Равновесные состояние системы. Понятие фазового пространства и его свойства..

3.2. Элементы теории вероятностей. Случайные величины и их описание. Функция распределения. Средние значения, математическое ожидание, дисперсия и флуктуации. Биноминальное распределение. Распределение в системах с большим количеством элементов Распределение Пуассона и Гаусса.

3.3. Статистические распределения для идеального газа.

Координата и скорость молекулы как случайные величины. Фазовое пространство координат и импульсов, обобщённые координаты. Функция Гамильтона. Каноническое распределение Гиббса. Распределение молекул по скоростям Максвелла. Закон распределения энергии по степеням свободы. Термодинамическая система в поле внешних сил. Идеальный газ в гравитационном поле, распределение Максвелла- Больцмана .

Раздел 4..Элементы статистической термодинамики

4.1. Основные положения статистической термодинамики. Условия равновесия.. Начала термодинамики.

4.2. Термодинамические процессы. Превращение тепла в работу. Циклические процессы. Энтропия и энергия. «Энтропийная» формулировка второго начала термодинамики. Энтропия и вероятность, статистический смысл энтропии. Парадокс Максвелла. Информационный смысл энтропии

ПЕРЕЧЕНЬ ОСНОВНОЙ И ДОПОЛНИТЕЛЬНОЙ ЛИТЕРАТУРЫ

1. Савельев И.В. Курс общей физики. Т. 1, 2, . - М.: Наука, 1980.

2. Сивухин Д.В. Общий курс физики. Т. 1,2. М., 1974-1980.

3. Стратонович Р.Л, Поляков М.С.. Элементы молекулярной физики, термодинамики и статистической физики. Изд. МГУ,1981.

4. Ф. Рейф. Статистическая физика. ВКФ. Изд. «Наука», М.,1977.