Тихонова Ольга Александровна

АВТОНОМНАЯ НЕКОММЕРЧЕСКАЯ ОРГАНИЗАЦИЯ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

ЦЕНТРОСОЮЗА РОССИЙСКОЙ ФЕДЕРАЦИИ

«РОССИЙСКИЙ УНИВЕРСИТЕТ КООПЕРАЦИИ»

КАЗАНСКИЙ КООПЕРАТИВНЫЙ ИНСТИТУТ (ФИЛИАЛ)

О.А.Тихонова

ЭКОНОМЕТРИКА

ТЕСТОВЫЕ ЗАДАНИЯ

для студентов по специальностям 080109.65 «Бухгалтерский учет, анализ и аудит»; 080105.65 «Финансы и кредит»

Казань

Тихонова О.А.. Эконометрика: Тестовые задания. - Казань: Казанский кооперативный институт, 2010. – 39с.

Тестовые задания по дисциплине «Эконометрика» для проверки остаточных знаний студентов по специальностям 080109.65 «Бухгалтерский учет, анализ и аудит»; 080105.65 «Финансы и кредит» составленыТихоновой О.А., старшим преподавателем кафедры «Инженерно-технические дисциплины и сервис» Казанского кооперативного института, в соответствии с требованиями по подготовке специалистов по специальностям 080109.65 «Бухгалтерский учет, анализ и аудит»; 080105.65 «Финансы и кредит» и инструкцией по разработке аттестационных педагогических измерительных материалов.

Рецензент: к.ф-м.н., доцент З.Э. Хайруллин

Тестовые задания:

согласованыс кафедрой «Бухгалтерский учет, анализ и аудит»

Зав. кафедрой М.Н. Хабриева

«10» сентября 2010 г.

обсуждены и рекомендованык изданию решением кафедры «Инженерно-технические дисциплины и сервис» от 07.10.2010 г., протокол №2

Зав. кафедрой Э.А. Гатина

одобреныМетодическим советом института от 07.10.2010 г., протокол №3

Председатель З.Н. Мирзагалямова

©Казанский кооперативный институт (филиал) Российского университета кооперации, 2010

©Тихонова О.А., 2010

S: Эконометрика – это …

+: наука, которая дает количественное выражение взаимосвязей экономических явлений и процессов

-: раздел экономической теории, связанный с анализом статистической информации

-: специальный раздел математики, посвященный анализу экономической информации

-: наука, которая осуществляет качественный анализ взаимосвязей экономических явлений и процессов

I:

S: Термин эконометрика был введен:

+: Фришем

-: Марковым

-: Тинбергеном

-: Фишером

I:

S: Значения экономических параметров, характеризующих различные экономические объекты в данный или один и тот же момент времени принято называть:

+: пространственными данными

-: временными данными или рядами

I:

S: Значения экономических параметров, характеризующих один и тот же экономический объект в различные моменты времени принято называть:

-: пространственными данными

+: временными данными или рядами

I:

S: Внешние по отношению к рассматриваемой экономической модели переменные называются:

-: эндогенные

+: экзогенные

-: лаговые

-: интерактивные

I:

S: Переменные, значения которых формируются внутри самой модели и являются объясняемыми, называются:

+: эндогенными

-: экзогенными

-: лаговыми

-: предопределенными

I:

S: Переменные, значения которых датированы предыдущими моментами времени, называются:

-: эндогенными

-: экзогенными

+: лаговыми

-: предопределенными

I:

S: Переменные, значения которых известны к моменту моделирования, называются:

-: эндогенными

-: экзогенными

-: лаговыми

+: предопределенными

I:

S: К классу предопределенных переменных не относят:

-: лаговые эндогенные

-: лаговые экзогенные

+: текущие эндогенные

-: текущие экзогенные

I:

S: Выберите правильную последовательность.

Этапы построения эконометрической модели:

1) оценка параметров модели (параметризация)

2) спецификация модели (выбор формы модели)

3) проверка адекватности модели

4) сбор статистической информации об объекте исследования

+: 2,4,1,3

-: 1,2,3,4

-: 2,4,3,1

-: 3,2,4,1

I:

S: Под верификацией модели понимается:

-: спецификация модели (выбор формы модели)

-: оценка параметров модели (параметризация)

-: сбор статистической информации об объекте исследования

+: проверка адекватности модели

I:

S: Под параметризацией (настройкой) модели понимается:

-: спецификация модели

+: оценка параметров модели

-: сбор статистической информации об объекте исследования

-: проверка адекватности модели

I:

S: Выбор списка переменных модели и типа взаимосвязи между ними выполняется на этапе:

+: спецификации

-: оценки параметров

-: сбора статистической информации об объекте исследования

-: проверка адекватности

I:

S: Статистический анализ модели (статистическое оценивание её параметров) относится к этапу:

-: априорному

-: информационному

+: идентификации

-: верификации

I:

S: Метод наименьших квадратов может применяться в случае

-: только парной регрессии

-: только множественной регрессии

+: нелинейной и линейной множественной регрессии

-: коллинеарной регрессии

I:

S: Метод наименьших квадратов используется для оценивания

+: параметров линейной регрессии

-: величины коэффициента корреляции

-: величины коэффициента детерминации

-: средней ошибки аппроксимации

I:

S: Параметры модели линейной парной регрессии y=a+b×x могут быть найдены

-: методом скользящей средней

+: методом наименьших квадратов

-: методом аналитического выравнивания

I:

S: Модель линейной парной регрессии имеет вид y=-5.79+36.84×x, коэффициент регрессии в такой модели равен:

-: -5.79

+: 36.84

-: 0.6

I:

S: Модель линейной парной регрессии имеет вид y=1.9+0.65×x, коэффициент регрессии в такой модели равен:

-: 1.9

+: 0.65

-: 0.55

I:

S: Модель линейной парной регрессии имеет вид y=3.4+2.986×x, коэффициент регрессии в такой модели равен:

-: 3.4

+: 2.986

-: 0.986

I:

S: Величина коэффициента регрессии показывает …

+: среднее изменение результата при изменении фактора на одну единицу

-: характер связи между фактором и результатом

-: тесноту связи между фактором и результатом

-: тесноту связи между исследуемыми факторами

I:

S: В зависимости от типа взаимосвязи между эндогенной переменной и экзогенной регрессионные модели подразделяются на:

+: линейные и нелинейные

-: парные и множественные

I:

S: В зависимости от количества экзогенных переменных в модели их подразделяются на:

-: линейные и нелинейные

+: парные и множественные

-: статические и динамические

-: стационарные и нестационарные

I:

S: Выбрать правильный ответ.

Независимые переменные в регрессионных моделях называются:

-: откликами

-: возмущениями

+: регрессорами

-: остатком

I:

S: Оценка случайного возмущения называется:

+: остатком

-: откликом

-: регрессором

I:

S: Выбрать правильный ответ.

Уравнение линейной парной регрессии между зависимой переменной Y и независимой переменной X, где a, b – параметры модели, может иметь вид:

+: Y=a+bX

-: Y=a+bX²

-: Y=a+b₁X₁+b₂X₂

I:

S: Уравнение линейной парной регрессии между зависимой переменной Y и независимой переменной X, где a, b – параметры модели, не может иметь вид:

-:Y=a+bX

+: Y=a+bX²

-: Y= bX

I:

S: Уравнение линейной парной регрессии между зависимой переменной Y и независимой переменной X, где a, b – параметры модели, может иметь вид:

-: Y=a+bX²

+: Y=a+bX

-: Y=a+b₁X₁+b₂X₂

-: Y=a+ b/X

I:

S: Уравнение линейной парной регрессии между зависимой переменной Y и независимой переменной X, где a, b – параметры модели, не может иметь вид:

+: Y=a+bX²

-: Y=a+bX

-: Y= bX

I:

S: Какое из уравнений соответствует уравнению модели линейной парной регрессии?

+: y=a+bx

-: y=a+b₁x₁+b₂x₂+e

-: y=a+b/x+e

-: y=a+b₁x+b₂x²+e

I:

S: Примером линейной зависимости экономических показателей является

-: классическая гиперболическая зависимость спроса от цены

+: зависимость зарплаты рабочего от его выработки при сдельной оплате труда

-: зависимость объема продаж от недели реализации

I:

S: Примером линейной зависимости экономических показателей является

+: зависимость стоимости квартиры от ее площади

-: зависимость зарплаты рабочего от номера месяца в течение года

-:зависимость объема продаж от недели реализации

V2: Модель линейной множественной регрессии

I:

S: Уравнение линейной множественной регрессии между зависимой переменной Y и независимой переменной X, где a, b – параметры модели, может иметь вид:

-: Y=a+bX

-: Y=a+bX²

+: Y=a+b₁X₁+b₂X₂

-: Y= bX

I:

S: Уравнение линейной множественной регрессии между зависимой переменной Y и независимой переменной X, где a, b – параметры модели, не может иметь вид:

+: Y=a+b₁X₁²+b₂X₂³

-: Y=a+b₁X₁+b₂X₂

-: Y=a+b₁X₁+b₂X₂+b₃X₃

I:

S: Какое из уравнений соответствует модели линейной множественной регрессии?

-: y=a+bx

+: y=a+b₁x₁+b₂x₂+e

-: y=a+b₁x+b₂x²+e

I:

S: Какие из уравнений не соответствуют модели линейной множественной регрессии?

-: y= a+b₁x₁+b₂x₂+b₃x₃+e

-: y=a+b₁x₁+b₂x₂+e

+: y=a+b₁x+b₂x²+e

I:

S: Нелинейным является уравнение регрессии нелинейное относительно входящих в него

+: переменных(факторов)

-: результатов

-: параметров

-: случайных величин

I:

S: Примером нелинейной зависимости экономических показателей является

+: классическая гиперболическая зависимость спроса от цены

-: линейная зависимость выручки от величины оборотных средств

-: зависимость объема продаж от недели реализации

-: линейная зависимость затрат на производство от объема выпуска продукции

I:

S: Линеаризация нелинейной модели регрессии может быть достигнута:

-: отбрасыванием нелинейных переменных

-: перекрестной суперпозицией переменных

+: преобразованием анализируемых переменных

-: сглаживанием переменных

I:

S: При помощи какого математического преобразования можно выполнить линеаризацию модели y=a+b×x³:

-: путем дифференцирования

-: путем логарифмирования

+: путем замены переменных

-: путем потенцирования

I:

S: При помощи какого математического преобразования можно выполнить линеаризацию модели y=a+b×lnx:

-: путем дифференцирования

-: путем логарифмирования

+: путем замены переменных

-: путем потенцирования

I:

S: При помощи какого математического преобразования можно выполнить линеаризацию модели y=a+b/x:

-: путем дифференцирования

-: путем логарифмирования

+: путем замены переменных

-: путем потенцирования

I:

S: При помощи какого математического преобразования можно выполнить линеаризацию модели y=а×b^x

-: путем дифференцирования

+: путем логарифмирования

-: путем замены переменных

-: путем потенцирования

I:

S: При помощи какого математического преобразования можно выполнить линеаризацию модели y= а×x^b:

-: путем дифференцирования

+: путем логарифмирования

-: путем замены переменных

-: путем потенцирования

I:

S: При помощи какого математического преобразования можно выполнить линеаризацию модели y=а×e^bx:

-: путем дифференцирования

+: путем логарифмирования

-: путем замены переменных

-: путем потенцирования

I:

S: К линейному уравнению нельзя привести следующий вид модели

+: y=a+bx^C

-: y=a+b₁x₁+b₂x₂+e

-: y=a+b/x+e

-: y=a+b₁x+b₂x²+e

I:

S: Теснота статистической связи между переменной у и объясняющими переменными Х измеряется:

-: t-критерием Стьюдента

-: коэффициентом детерминации

+: коэффициентом корреляции

-: F-критерием Фишера

I:

S: Коэффициент парной линейной корреляции характеризует:

+: тесноту линейной связи между двумя переменными

-: тесноту нелинейной связи между двумя переменными

-: тесноту линейной связи между несколькими переменными

-: тесноту нелинейной связи между несколькими переменными

I:

S: Корреляция подразумевает наличие связи между

+: переменными

-: параметрами

-: случайными факторами

-: результатом и случайными факторами

I:

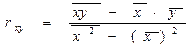S:
Коэффициент корреляции для модели линейной парной регрессии может быть рассчитан по формуле:

-:

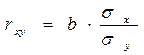-: R=(r_xy)²

+:

I:

S: Линейный коэффициент корреляции r_xy может принимать значения в диапазоне:

-: (-1; 1)

-: [0; 1]

+: [-1; 1]

-: [-1.1; 1]

I:

S: Линейный коэффициент корреляции r_xy не может принимать значения в диапазоне:

+: (-2; 1)

-: [0; 1]

-:[-1; 1]

-: [-0.1; 1]

I:

S: Линейный коэффициент корреляяции r_xy может принимать значения в диапазоне:

-: (-1; 1.1)

-: [0; 1.5]

-: [0; 2]

+: [-1; 1]

I:

S: Линейный коэффициент корреляции r_xy может принимать значения в диапазоне:

-: [0; 1.5]

-: [0; 1.1]

+: [-1; 1]

-: [-0.5; 1.5]

I:

S: Линейный коэффициент корреляции r_xy может принимать значения только в диапазоне:

-: [-1; 1.5]

-: [-1.1; 1]

-: [-1.1; 1]

+: [-1; 1]

I:

S: Линейный коэффициент корреляции r_xy не может принимать значение равное:

-: 0.5

-: 0.99

-: -0.5

+: 1.2

I:

S: Линейный коэффициент корреляции r_xy не может принимать значение равное:

-: 0.5

-: 0.99

+: 1.05

-: 1

I:

S: Линейный коэффициент корреляции r_xy не может принимать значение равное:

-: 0.6

-: 0.01

+: -1.05

-: 1

I:

S: Линейный коэффициент корреляции r_xy может принимать значение равное:

-: -1.1

+: 0.99

-: 1.05

-: 1.2

I:

S: Линейный коэффициент корреляции r_xy может принимать значение равное:

-: -1.35

+: -0.99

-: 1.05

-: 1.001

V2:

I:

S: Корреляционная связь между переменными X и Y считается тесной, если коэффициент корреляции принимает следующие значения:

-: r_xy=0;

-: 0<r_xy£0.3

-: 0.3<r_xy£0.7

+: 0.7<r_xy<1

-: r_xy=1

I:

S: Корреляционная связь между переменными X и Y считается умеренной, если коэффициент корреляции принимает следующие значения:

-: r_xy=0;

-: 0<r_xy£0.3

+: 0.3<r_xy£0.7

-: 0.7<r_xy<1

-: r_xy=1

I:

S: Корреляционная связь между переменными X и Y считается слабой, если коэффициент корреляции принимает следующие значения:

-: r_xy=0;

+: 0<r_xy£0.3

-: 0.3<r_xy£0.7

-: 0.7<r_xy<1

-: r_xy=1

I:

S: Корреляционная связь между переменными X и Y считается линейной функциональной, если коэффициент корреляции принимает следующие значения:

-: r_xy=0;

-: 0<r_xy£0.3

-: 0.3<r_xy£0.7

-: 0.7<r_xy<1

+: r_xy=1

I:

S: Корреляционная связь между переменными X и Y отсутствует, если коэффициент корреляции принимает следующие значения:

-: r_xy=0;

-: 0<r_xy£0.3

-: 0.3<r_xy£0.7

+: 0.7<r_xy<1

-: r_xy=1

I:

S: Коэффициент детерминации R является показателем

-: тесноты связи между переменными X и Y

+: качества построенной модели

-: адекватности модели исходным фактическим данным

-: статистической значимости модели

I:

S: Коэффициент детерминации рассчитывается для оценки качества

+: подбора уравнения регрессии

-: параметров уравнения регрессии

-: мультиколлинеарных факторов

-: факторов, не включенных в уравнение регрессии

I:

S: Качество построенной модели парной регрессии может быть измерено:

-: t-критерием Стьюдента

+: коэффициентом детерминации

-: коэффициентом корреляции

-: F-критерием Фишера

I:

S: Коэффициент детерминации для модели линейной парной регрессии может быть рассчитан по формуле:

-:

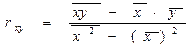+: R=(r_xy)²

-:

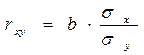I:

S: Линейный коэффициент детерминации R может принимать значения в диапазоне:

-: (-1; 1)

+: [0; 1]

-: [-1; 1]

-: [-1.1; 1]

I:

S: Линейный коэффициент детерминации R не может принимать значения в диапазоне:

+: (1; 1.5)

-: [0; 1]

-: [0; 0.99]

-: [0.1; 1]

I:

S: Линейный коэффициент детерминации R может принимать значения в диапазоне:

-: (-1; 1)

-: [0; 1.5]

+: [0; 1]

-: [-1.1; 1]

I:

S: Линейный коэффициент детерминации R может принимать значения в диапазоне:

+: [0; 1]

-: [0; 1.1]

-: [-1; 1]

-: [-0.5; 1]

I:

S: Линейный коэффициент детерминации R может принимать значения только в диапазоне:

-: [-1; 1]

-: [-1.1; 1]

-: [-1; 1]

+: [0; 1]

I:

S: Линейный коэффициент детерминации R не может принимать значение равное:

-: 0.5

-: 0.99

+: -0.5

-: 1

I:

S: Линейный коэффициент детерминации R не может принимать значение равное:

-: 0.5

-: 0.99

+: 1.05

-: 1

I:

S: Линейный коэффициент детерминации R не может принимать значение равное:

-: 0.6

-: 0.01

+: -1.05

-: 1

I:

S: Линейный коэффициент детерминации R может принимать только значение равное:

-: -0.5

+: 0.99

-: 1.05

-: 1.2

I:

S: Линейный коэффициент детерминации R может принимать только значение равное:

+: 0.35

-: -0.99

-: 1.05

-: 1.001

I:

S: Определить коэффициент детерминации линейной двухфакторной модели, если известно, что коэффициент корреляции r_xy= -0.5

-: 0.5

+: 0.25

-: -0.5

-: -0.25

I:

S: Определить коэффициент детерминации линейной двухфакторной модели, если известно, что коэффициент корреляции r_xy= -0.3

-: 0.3

+: 0.09

-: -0.3

-: -0.09

I:

S: Определить коэффициент детерминации линейной двухфакторной модели, если известно, что коэффициент корреляции r_xy= -0.4

-: 0.4

+: 0.16

-: -0.4

-: -0.16

I:

S: Определить коэффициент детерминации линейной двухфакторной модели, если известно, что коэффициент корреляции r_xy= -0.25

+: 0.0625

-: -0.625

-: 0.5

-: -0.25

I:

S: Определить коэффициент детерминации линейной двухфакторной модели, если известно, что коэффициент корреляции r_xy= -0.6

+: 0.36

-: -0.36

-: 0.6

-: -0.24

I:

S: Определить коэффициент детерминации линейной двухфакторной модели, если известно, что коэффициент корреляции r_xy= -0.7

-: 0.07

-: -0.49

+: 0.49

-: -0.7

I:

S: Определить коэффициент детерминации линейной двухфакторной модели, если известно, что коэффициент корреляции r_xy= 0.7

-: 0.07

-: -0.49

+: 0.49

-: -0.7

I:

S: Определить коэффициент детерминации линейной двухфакторной модели, если известно, что коэффициент корреляции r_xy= 0.8

+: 0.64

-: -0.64

-: 0.8

-: -0.8

I:

S: Определить коэффициент детерминации линейной двухфакторной модели, если известно, что коэффициент корреляции r_xy= 0.9

-: -0.81

+: 0.81

-: 0.9

-: -0.9

I:

S: Определить коэффициент детерминации линейной двухфакторной модели, если известно, что коэффициент корреляции r_xy= 0.65

-: -0.65

-: 0.65

+: 0.4225

-: -0.125

I:

S: Тенденция (Тренд) временного ряда характеризует совокупность факторов,

+: оказывающих долговременное влияние и формирующих общую динамику изучаемого показателя

-: оказывающих сезонное воздействие

-: оказывающих единовременное влияние

-: не оказывающих влияние на уровень ряда

I:

S: Плавно меняющаяся компонента временного ряда, отражающая влияние на экономические показатели долговременных факторов, называется:

+: трендом

-: сезонной компонентой

-: циклической компонентой

-: случайной компонентой

I:

S: Компонента временного ряда, которая отражает колебания экономических показателей с периодом равным одному году, называется:

-: трендом

+: сезонной компонентой

-: циклической компонентой

-: случайной компонентой

I:

S: Компонента временного ряда, которая отражает колебания экономических показателей с периодами длиной в несколько лет, называется:

-: трендом

-: сезонной компонентой

+: циклической компонентой

-: случайной компонентой

I:

S: Компонента временного ряда, которая отражает влияние не поддающихся учету и регистрации случайных факторов, называется:

-: трендом

-: сезонной компонентой

-: циклической компонентой

+: случайной компонентой

I:

S: Временной ряд называется стационарным, если

+: среднее значение членов ряда постоянно

-: члены ряда образуют арифметическую прогрессию

-: члены ряда образуют геометрическую прогрессию

-: среднее значение членов ряда постоянно растет

I:

S: Временной ряд является нестационарным, если:

-: среднее значение его членов постоянно

-: его случайная составляющая зависит от времени

-: его члены не зависят от времени

+: его неслучайная составляющая зависит от времени

I:

S: В стационарном временном ряде трендовая компонента

+: отсутствует+

-: присутствует

-: имеет линейную зависимость от времени

-: имеет нелинейную зависимость от времени

I:

S: В аддитивной модели временного ряда его основные компоненты

-: перемножаются

-: логарифмируются

+: складываются

-: закономерные компоненты перемножаются, а случайная - складывается

I:

S: В мультипликативной модели временного ряда его основные компоненты

-: логарифмируются

+: перемножаются

-: складываются

-: закономерные компоненты перемножаются, а случайная - складывается

I:

S: В мультипликативно-аддитивной модели временного ряда его основные компоненты

-: логарифмируются

-: перемножаются

-: складываются

+: закономерные компоненты перемножаются, а случайная - складывается;

I:

S: Временной ряд записан в следующем виде: Y=T+S+C+E, выберите вид соответствующей модели:

-: регрессионная модель

-: мультипликативная модель

-: мультипликативно-аддитивная модель

+: аддитивная модель

I:

S: Временной ряд записан в следующем виде: Y=T×S×C×E, выберите вид соответствующей модели:

-: регрессионная модель

+: мультипликативная модель

-: мультипликативно-аддитивная модель

-: аддитивная модель

I:

S: Временной ряд записан в следующем виде: Y=T×S×C+E, выберите вид соответствующей модели:

-: регрессионная модель

-: мультипликативная модель

+: мультипликативно-аддитивная модель

-: аддитивная модель

I:

S: Какой из методов используется при вычислении сезонной компоненты временного ряда:

-: метод укрупнения интервалов

+: метод скользящей средней

-: метод экспоненциального сглаживания

I:

S: Какие методы используются при моделировании тренда временного ряда?

+: метод укрупнения интервалов

+: метод скользящей средней

+: метод аналитического выравнивания

-: графический метод

I:

S: Какой метод не используется при моделировании тренда временного ряда?

-: метод укрупнения интервалов

-: метод скользящей средней

-: метод аналитического выравнивания

+: графический метод

I:

S: Система одновременных уравнений может быть записана в виде:

+: структурной формы

-: функциональной формы

+: приведенной формы

-: обобщенной формы

I:

S: Набор взаимосвязанных регрессионных моделей, в которых одни и те же переменные могут одновременно быть эндогенными в одних уравнениях и экзогенными в других уравнениях называется:

-: системой рекурсивных уравнений

-: системой независимых уравнений

+: системой одновременных уравнений

-: системой уравнений с фиксированным набором факторов

I:

S: Система уравнений, в которой каждая зависимая переменная (у_j) рассматривается как функция одного и того же набора факторов (х_i), при этом каждое уравнение системы может рассматриваться самостоятельно, называется:

-: системой рекурсивных уравнений

+: системой независимых уравнений

-: системой одновременных уравнений

-: системой уравнений с фиксированным набором факторов

I:

S: Система уравнений, в которой зависимая переменная у включает в каждое последующее уравнение в качестве факторов все зависимые переменные из предшествующих уравнений наряду с набором собственных факторов х. (Каждое уравнение этой системы можно рассматривать самостоятельно, каждая зависимая переменная (у_j) рассматривается как функция одного и того же набора факторов (х_i)) называется:

+: системой рекурсивных уравнений

-: системой независимых уравнений

-: системой одновременных уравнений

-: системой уравнений с фиксированным набором факторов

I:

S: Система уравнений, в которой одни и те же зависимые переменные в одних уравнениях входят в левую часть, а в других уравнениях – в правую часть системы:

-: системой рекурсивных уравнений

-: системой независимых уравнений

+: системой одновременных уравнений

-: системой уравнений с фиксированным набором факторов

I:

S: Форма записи эконометрической модели в виде:

y₁=d₁₁x₁+d₁₂x₂+e₁

y₂=d₂₁x₁+d₂₂x₂+e₂

называется

-: структурной формой

+: приведенной формой

-: редуцированной формой

-: нормальной формой

I:

S: В правой части приведенной формы системы одновременных уравнений могут стоять только…….. переменные

+: экзогенные

-: лаговые

-: эндогенные

-: нелаговые

I:

S: Форма записи эконометрической модели в виде:

y₁=a₁₁x₁+ a₁₂x₂+b₁₂y₂+e₁

y₂= a₂₁x₁+ a₂₂x₂+b₂₁y₁+e₂

называется

+: структурной формой;+

-: приведенной формой;

-: редуцированной формой;

-: нормальной формой;

I:

S: В левой части структурной формы системы одновременных уравнений могут стоять только…….. переменные

-: экзогенные

-: лаговые

+: эндогенные

-: нелаговые

I:

S: Ниже приводится макроэкономическая модель:

Функция потребления: C_t=a₀ +a₁Y_t+a₂Y_t-1 +u₁

Функция инвестиций: I_t= b₀+b₁Y_t+u₂

Тождество дохода: Y_t=C_t+I_t+G_t,

где C_t, - расходы на конечное потребление в период t;

Y_t, Y_t-1 – доход в годы t и t-1;

I_t- валовые инвестиций в году t;

G_t – государственные расходы году t;

u₁, u₂ – случайные ошибки.

Определить количество эндогенных (зависимых) переменных в модели:

-: 2;

+: 3;+

-: 4;

-: 7;

I:

S: Ниже приводится макроэкономическая модель:

Функция потребления: C_t=a₀ +a₁Y_t+a₂Y_t-1 +u₁

Функция инвестиций: I_t= b₀+b₁Y_t+u₂

Тождество дохода: Y_t=C_t+I_t+G_t,

где C_t, - расходы на конечное потребление в период t;

Y_t, Y_t-1 – доход в годы t и t-1;

I_t- валовые инвестиций в году t;

G_t – государственные расходы году t;

u₁, u₂ – случайные ошибки.

Определить количество экзогенных (независимых) переменных в модели:

+: 2

-: 3

-: 4

-: 7

I:

S: Ниже приводится макроэкономическая модель:

Функция денежного рынка: R_t=a₀ +a₁Y_t+a₂M_t +u₁

Функция товарного рынка: Y_t= b₀+b₁R_t+ b₂G_t +u₂

Функция инвестиций: I_t= c₀+c₁R_t + u₃,

где R_t – процентная ставка в период t;

Y_t – реальный валовый национальный доход в период t;

I_t- внутренние инвестиции в году t;

M_t- денежная масса в период t;

G_t – государственные расходы году t;

u₁, u₂, u₃– случайные ошибки.

Определить количество эндогенных (зависимых) переменных в модели:

-: 2

+: 3

-: 4

-: 7

I:

S: Ниже приводится макроэкономическая модель:

Функция денежного рынка: R_t=a₀ +a₁Y_t+a₂M_t +u₁

Функция товарного рынка: Y_t= b₀+b₁R_t+ b₂G_t +u₂

Функция инвестиций: I_t= c₀+c₁R_t + u₃,

где R_t – процентная ставка в период t;

Y_t – реальный валовый национальный доход в период t;

I_t- внутренние инвестиции в году t;

M_t- денежная масса в период t;

G_t – государственные расходы году t;

u₁, u₂, u₃– случайные ошибки.

Определить количество экзогенных (независимых) переменных в модели:

+: 2

-: 3

-: 4

-: 7

I:

S: Ниже приводится макроэкономическая модель, характеризующая спрос на продукцию:

Q_t=a₀ +a₁Y_t +u₁

C_t= b₀+b₁Y_t +u₂

I_t=c₀+c₁(Y_t-1-K_t-1)+u₃

Y_t=C_t+I_t

K_t=K_t-1+I_t

где Q_t –реализованная продукция в период t;

Y_t, Y_t-1 –валовая добавленная стоимость в периоды t и t-1;

I_t – валовые инвестиции в регион в году t;

K_t, K_t-1 – реальный запас капитала в регионе на конец периода t и t-1;

u₁, u₂, u₃, – случайные ошибки

Определить количество эндогенных (зависимых) переменных в модели:

-: 3

-: 4

+: 5

-: 7

I:

S: Ниже приводится макроэкономическая модель, характеризующая спрос на продукцию:

Q_t=a₀ +a₁Y_t +u₁

C_t= b₀+b₁Y_t +u₂

I_t=c₀+c₁(Y_t-1-K_t-1)+u₃

Y_t=C_t+I_t

K_t=K_t-1+I_t

где Q_t –реализованная продукция в период t;

Y_t, Y_t-1 –валовая добавленная стоимость в периоды t и t-1;

I_t – валовые инвестиции в регион в году t;

K_t, K_t-1 – реальный запас капитала в регионе на конец периода t и t-1;

u₁, u₂, u₃, – случайные ошибки

Определить количество экзогенных (независимых) переменных в модели:

-: 7

-: 4

-: 5

+: 2

I:

S: Ниже приводится макроэкономическая модель спроса и предложения кейнсианского типа:

Q_t^S=a₀ +a₁P_t + a₂P_t-1 +u₁ (предложение)

Q_t^d= b₀+b₁P_t + b₂P_t + b₃Y_t +u₂ (спрос)

Q_t^S=Q_t^d (тождество)

где Q_t^d –спрос на товар в период t;

Q_t^S предложение товара в момент t;

Р_t –цена товара в моменты t и t-1;

У_t –доход в момент t;

u1, u₂– случайные ошибки.

Определить количество эндогенных (зависимых) переменных в модели:

+: 2

-: 4

-: 5

-: 7

I:

S: Ниже приводится макроэкономическая модель спроса и предложения кейнсианского типа:

Q_t^S=a₀ +a₁P_t + a₂P_t-1 +u₁ (предложение)

Q_t^d= b₀+b₁P_t + b₂P_t + b₃Y_t +u₂ (спрос)

Q_t^S=Q_t^d (тождество)

где Q_t^d –спрос на товар в период t;

Q_t^S предложение товара в момент t;

Р_t –цена товара в моменты t и t-1;

У_t –доход в момент t;

u1, u₂– случайные ошибки.

Определить количество экзогенных (независимых) переменных в модели:

+: 2

-: 4

-: 5

-: 7

I:

S: Ниже приводится макроэкономическая модель, характеризующая денежный рынок:

R_t=a₁ +b₁₁M_t + b₁₂Y_t +u₁

C_t= a₂+b₂₁R_t + b₂₂I_t +u₂,

где R_t –процентная ставка в период t;

Y_t –ВВП в период t;

М – денежная масса,

I_t – внутренние инвестиции году t;

u₁, u₂, u₃, – случайные ошибки.

Определить количество эндогенных (зависимых) переменных в модели:

+: 2

-: 4

-: 5

-: 7

I:

S: Ниже приводится макроэкономическая модель, характеризующая денежный рынок:

R_t=a₁ +b₁₁M_t + b₁₂Y_t +u₁

C_t= a₂+b₂₁R_t + b₂₂I_t +u₂,