Основы дискретной математики
Множества и отношения. Свойства отношений. Операции над множествами.
Студент должен:
иметь представление:
· о способах задания множеств;
· о диаграммах Эйлера.
знать:
· определение множества, отношений;
· операции и свойства операций над множествами;
· свойства отношений.
Элементы и множества. Задание множеств. Операции над множествами. Свойства операций над множествами. Отношения. Свойства отношений.
Основные понятия теории графов.
Студент должен:
иметь представление:
· о связи понятия графов и понятия отношения.
знать:
· определение графов и его элементов;
· виды графов и операции над ними.
Графы. Основные определения. Элементы графов. Виды графов и операции над ними.
ОСНОВЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ.
Вероятность. Теоремы сложения и умножения вероятностей.
Студент должен:
знать:
· понятия: событие, частота и вероятность появления события, совместные и несовместные события, полная вероятность;
· теоремы сложения вероятностей;
· теоремы умножения вероятностей.
уметь:
· находить вероятность в простейших задачах, используя классическое определение
вероятности;
· решать задачи с применением теорем сложения и умножения вероятностей.
Понятие события и вероятности события. Достоверные и невозможные события. Классическое определение вероятности. Теоремы сложения вероятностей. Теоремы умножения вероятностей.
Случайная величина, ее функция распределения.
Студент должен:
знать:
· способы задания случайной величины;
· определение дискретной и непрерывной случайной величины;
· закон распределения случайной величины.
уметь:
· строить ряд распределения случайной величины;
· находить функцию распределения случайной величины.
Случайная величина. Дискретная и непрерывная случайные величины. Закон распределения случайной величины.
Математическое ожидание и дисперсия случайной величины.
Студент должен:
знать:
· определения числовых характеристик случайной величины: математического ожидания, дисперсии дискретной случайной величины;
· определение квадратичного отклонения случайной величины.
уметь:
· находить математическое ожидание и дисперсию случайной величины по заданному закону ее распределения;
· находить среднее квадратичное отклонение случайной величины.
Математическое ожидание и дисперсия случайной величины. Среднее квадратичное отклонение случайной величины.
Основные численные методы
Численное интегрирование
Студент должен:
знать:
· способы представления функции в виде прямоугольников и трапеций;
· формулу Симпсона;
· выражения для определения предельных абсолютных погрешностей;
уметь:
· вычислять интегралы по формулам прямоугольников, трапеций по формуле Симпсона.
Формулы прямоугольников. Формула трапеций. Формула Симпсона. Абсолютная погрешность при численном интегрировании.
Численное дифференцирование
Студент должен:
знать:
· интерполяционные формулы Ньютона;
· таблицу конечных разностей;
уметь:
· по табличным данным находить аналитическое выражение производной.
Численное дифференцирование. Формулы приближенного дифференцирования, основанные на интерполяционных формулах Ньютона. Погрешность в определении производной.
Примеры решения упражнений
Пример 1.
Вычислите пределы фукций: 1) 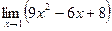 ; 2)
; 2) 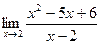 ; 3)
; 3) 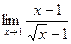 .
.
Решение.
1) 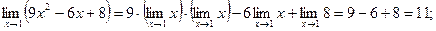
2) Поскольку предел знаменателя равен 0, то воспользоваться теоремой о пределе частного невозможно. Поэтому первоначально сократим дробь, разложив числитель на множители:
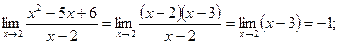
3)
| |
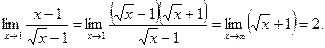
Ответ. 1) 11, 2) –1, 3) 2.
Пример 2.
Найдем производные следующих функций:
1) 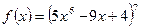 ;
;
2) 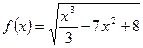 ;
;
3) 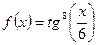 .
.
Решение.
1) Полагаем, что 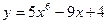 , тогда
, тогда 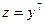 . Отсюда, согласно формуле для расчета производной сложной функции, имеем:
. Отсюда, согласно формуле для расчета производной сложной функции, имеем:
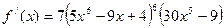 .
.
2) Полагаем, что 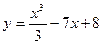 , тогда
, тогда 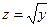 . Отсюда, согласно формуле для расчета производной сложной функции, имеем:
. Отсюда, согласно формуле для расчета производной сложной функции, имеем:
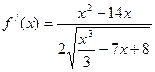 .
.
3) Имеем, что
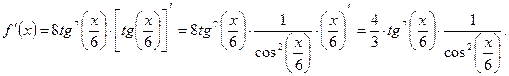
Пример 3.
Исследуем функцию и построим эскиз ее графика:
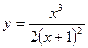
Решение.
1. Определим область существования этой функции. Функция существует при всех значениях х, кроме 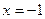 , при котором знаменатель дроби обращается в нуль. Значит, функция определена в интервалах (—
, при котором знаменатель дроби обращается в нуль. Значит, функция определена в интервалах (— 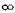 , —1)
, —1) 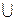 (—1, +
(—1, + 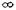 ).
).
2. Исследуем вопрос о наличии центра симметрии к оси симметрии. Проверим для этого, выполняются ли равенства 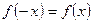 или
или 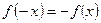 .
.
Непосредственная подстановка убеждает нас, что ни одно из этих равенств не выполняется, так что ни центра, ни оси симметрии график функции не имеет.
3. Определяем точки разрыва. Числитель и знаменатель дробно-рациональной функции 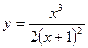 представляют собой непрерывные функции и, следовательно, функция у будет непрерывной при всех значениях х, кроме
представляют собой непрерывные функции и, следовательно, функция у будет непрерывной при всех значениях х, кроме 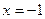 , при котором знаменатель дроби обращается в нуль.
, при котором знаменатель дроби обращается в нуль.
4. Переходим к определению асимптот графика.
а) Вертикальные асимптоты найдем, приравняв знаменатель нулю:
2(х+1)2 = 0; отсюда 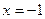 .
.
Вертикальная асимптота одна: ее уравнение 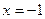 .
.
б) Горизонтальные асимптоты находим так: отыскиваем
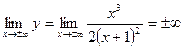 ,
,
а это означает, что горизонтальных асимптот нет.
в) Наклонные асимптоты:
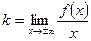
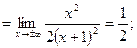
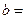
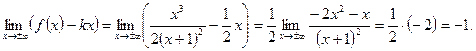
Наклонная асимптота одна: 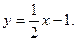
5 и 6. Определяем интервалы возрастания и убывания функции и экстремум функции.
Находим первую производную: 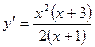 . Определим критические точки:
. Определим критические точки:
1) Решаем уравнение 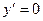 , т. е. уравнение
, т. е. уравнение 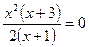 и находим, что
и находим, что 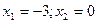 .
.
2) Определяем значения х, при которых 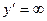 . Таким значением является
. Таким значением является 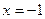 Но это значение не должно подлежать рассмотрению, так как оно не входит в область определения функции. Критические точки, подлежащие рассмотрению:
Но это значение не должно подлежать рассмотрению, так как оно не входит в область определения функции. Критические точки, подлежащие рассмотрению: 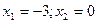 и точка
и точка 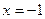 – разделяют область существования функции на такие интервалы:
– разделяют область существования функции на такие интервалы: 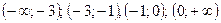 .
.
В каждом из этих интервалов производная сохраняет знак: в первом — плюс, во втором — минус, в третьем — плюс, в четвертом — плюс (в этом можно убедиться, взяв в каждом интервале произвольное значение х и вычислив при нем значение у'). Последовательность знаков первой производной запишется так: +, —, +, +. Значит, в интервале 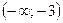 функция возрастает, в интервале
функция возрастает, в интервале 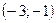 – убывает, в интервалах
– убывает, в интервалах 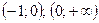 функция возрастает.
функция возрастает.
При 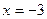 функция имеет максимум и
функция имеет максимум и 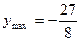 . Так как знаки во втором и третьем интервалах различны, то можно было бы предположить, что при
. Так как знаки во втором и третьем интервалах различны, то можно было бы предположить, что при 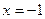 есть экстремум. Но такое предположение неверно, так как при
есть экстремум. Но такое предположение неверно, так как при 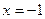 заданная функция не существует. Итак, функция имеет единственный экстремум (максимум) при
заданная функция не существует. Итак, функция имеет единственный экстремум (максимум) при 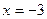 .
.
7. Определяем интервалы выпуклости и вогнутости графика функции и точек перегиба.
Находим, что 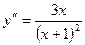 и определяем критические точки второго рода:
и определяем критические точки второго рода:
1) решаем уравнение 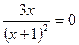 и находим, что
и находим, что 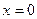 ;
;
2) определяем значения х, при котором 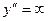 . Таким значением является
. Таким значением является 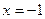 . Как уже было отмечено выше, это значение рассматриваться не должно, так как при нем не существует заданной функции.
. Как уже было отмечено выше, это значение рассматриваться не должно, так как при нем не существует заданной функции.
Критическая точка второго рода 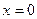 разделяет интервалы (—
разделяет интервалы (— 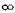 , —1) и (—1, +
, —1) и (—1, + 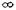 ). существования функции на интервалы:
). существования функции на интервалы: 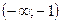 ,
, 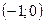 и
и 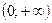 .
.
В каждом из этих интервалов вторая производная конечна и сохраняет знак: в первом – минус, во втором – минус, в третьем – плюс, и мы имеем такое чередование знаков второй производной в этих интервалах: —, —, +.
Значит, в интервалах 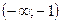 и
и 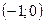 кривая выпукла, а в интервале
кривая выпукла, а в интервале
(0, + ∞) — вогнута. При 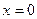 вторая производная равна нулю, а при переходе из второго интервала в третий она поменяла знак. Это указывает на то, что при
вторая производная равна нулю, а при переходе из второго интервала в третий она поменяла знак. Это указывает на то, что при 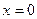 , кривая имеет точку перегиба. Координаты точки перегиба (0, 0) — это начало координат.
, кривая имеет точку перегиба. Координаты точки перегиба (0, 0) — это начало координат.
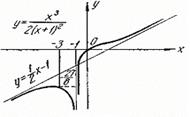 Рис. 9 Рис. 9 | 8. Определение точек пересечения графика с осями координат и исследование промежутков монотонности произведите самостоятельно. График функции пересекает оси координат в единственной точке 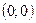 . Функция отрицательна на промежутках . Функция отрицательна на промежутках 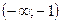 и и 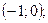 положительна на промежутке положительна на промежутке 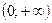 . . |
Все полученные сведения наносим на чертеж и получаем эскиз кривой (см. рис. 9).
Пример 4.
Найдем 1) 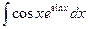 , 2)
, 2) 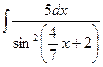
Решение.
1)
|
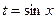 . Тогда
. Тогда 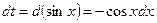
Произведя подстановку, получим:
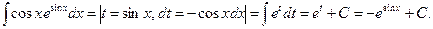
2) Так как аргумент подынтегральной функции имеет вид 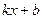 , где
, где 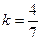 , то, применяя вышеназванную теорему, получим:
, то, применяя вышеназванную теорему, получим:
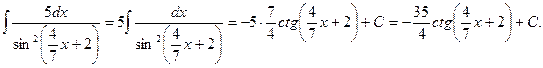
Пример 5.
Вычислим 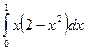 .
.
Решение.
Положим 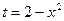 . Тогда
. Тогда 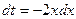 . Вычислим значения новых пределов интегрирования, подставив в формулу новой переменной исходные значения пределов:
. Вычислим значения новых пределов интегрирования, подставив в формулу новой переменной исходные значения пределов: 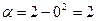 ,
, 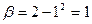 . Воспользовавшись формулой замены переменной в определенном интеграле, получим:
. Воспользовавшись формулой замены переменной в определенном интеграле, получим:
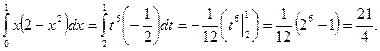
Пример 6.
Исследовать сходимость ряда, используя признак Даламбера:
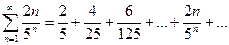
Решение. Подставив в общий член ряда 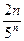 вместо n число n+1, получим
вместо n число n+1, получим 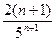 . Найдём предел отношения (n+1)-ого члена к n-му члену при
. Найдём предел отношения (n+1)-ого члена к n-му члену при 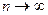 :
:
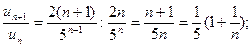
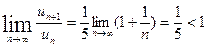 .
.
Следовательно, данный ряд сходится.
