Специальные свойства объектов подкласса ss

Свойство	Описание	Тип данных
a	Матрица состояний
b	Матрица вход-состояние
c	Матрица вход-состояние-выход	Двумерная матрица
d	Матрица вход-выход
e	Матрица при производных
StateName	Названия переменных состояний	Массив ячеек из строк

Отметим некоторые особенности используемых свойств lti-объектов.

Свойство variable для объектов подклассов tf и zpk задает способ отображения переменной при выводе передаточных функций на экран. По умолчанию такими переменными являются 's' (переменная преобразования Лапласа) для непрерывных систем и 'z' (переменная Z-преобразования) для дискретных систем. Альтернативными значениями переменной могут быть 'p' для 's' и 'q' или 'z^-1 для z. Отметим, что команда tf дает тот же результат, что и команда filt, когда свойство Variable имеет значение 'z^-1 или 'q'.

Свойство StateName позволяет присвоить имена переменным состояния.

При работе с ППП Control System Toolbox перечень свойств lti-объекта может быть просмотрен с помощью команд set(ss), set(tf), set(zpk).

Методические примеры

Требуется создать динамическую модель системы представленную передаточной функцией:

W(s)=(1)/(0.1s²+0.1s+1)

Создадим lti-объект с именем wn, для этого выполним:

>> wn=tf(1,[0.1 0.1 1])

Transferfunction

1

------------------

0.1s^2 + 0.1s+1

Определим корни характеристического уравнения:

>> pole(wn)

ans =

-0.5000 + 3.1225i

-0.5000 - 3.1225i

Так как действительная часть корней меньше нуля, то можно сделать вывод об асимптотической устойчивости рассматриваемой системы.

Требуется создать динамическую модель замкнутой системы представленную на рисунке 1.

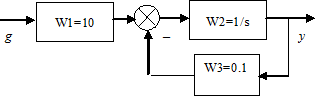
Рис. 2.1. Структурная схема системы автоматического регулирования

Создадим LTI-объект с именем wrez, для этого выполним следующие команды:

>> W1=tf([10],[1])

Transfer function:

>> W2=tf(1,[1 0])

Transfer function:

-

s

>> W3=tf(.1,1)

Transfer function:

0.1

>> wrez=W1*feedback(W2,W3)

Transfer function:

-------

s + 0.1

Построим переходную характеристику рассмотренной системы:

>> step(wrez)

На рисунке 2.2 показана переходная характеристика системы и найдено время регулирования (Settling Time).

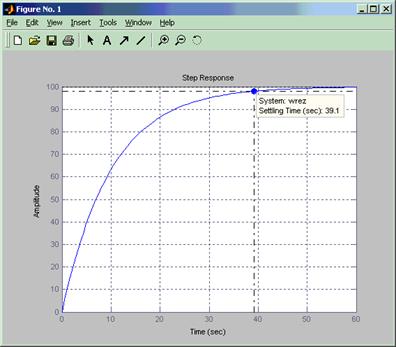
Рис. 2.2. Переходная характеристика системы wrez

Последовательность выполнения работы

1. Согласно заданному варианту организовать динамическую модель САР (см. рис. 2.3) в среде Matlab.

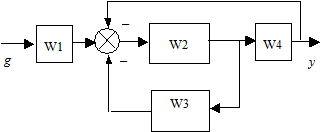
Рис. 2.3. Структурная схема системы исследования

Передаточные функции для каждого варианта приведены в таблице 2.6.

Таблица 2.6

Варианты заданий

Вариант	W1	W2	W3	W4
		100/s		10/(s+1)
		100/s		1/s
		10/(s+1)		1/s
		20/s	s/s+1	1/(s+1)
	1/(s+1)	1/s		1/s
	10/(0.1s+1)	1/(s+100)	10/s
	0.5/(s+1)	1/(s2+0.1s+1)
	0.1/(s+1)	1/(s2+1)
		1/(s2+0.1s+1)		10/s
	50/(s+1)		1/(s+1)
			20/(0.1s+1)	10/s
	10/(s+10)	10/(s+10)		10/(s+2)
		5/(0.1s+10)	10/(s+1)

2. Определить аналитически передаточную функцию замкнутой и разомкнутой системы САУ.

3. Сравнить полученные результаты.

4. Оценить устойчивость САУ корневым методом.

5. Определить нули полученной системы.

6. Построить переходную характеристику САУ.

7. Используя библиотеку динамических элементов Simulink организовать визуально-ориентированную модель согласно заданному варианту. Получить переходную характеристику. Сравнить полученный график переходного процесса с результатами моделирования с помощью Control System Toolbox.

Содержание отчета

Отчет оформляется в соответствии с требованиями, предъявляемыми к оформлению лабораторных работ в вузе, и должен содержать:

1. Титульный лист.

2. Формулировку цели работы.

3. Постановка задачи в соответствии с вариантом задания.

4. Результаты работы.

5. Выводы.

2.6. Контрольные вопросы

1. Дайте определение и поясните физический смысл переходной характеристики.

2. Представьте исходную систему в пространстве состояний.

3. Найдите передаточную функцию замкнутой системы.

4. Указать динамические свойства звеньев представленные в задании.

5. Какой класс систем позволяет моделировать библиотека Control System Toolbox?