Элементы теории вероятностей

Случайные события

Элементарным исходом называют любой простейший исход опыта.

Множество всех элементарных исходов называется пространством элементарных исходов: .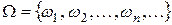

Класс A подмножеств множества 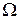называется алгеброй, если выполнены следующие аксиомы:

А1. 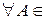A A,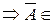

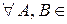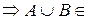А2. A 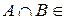A, A.

Класс подмножеств A называется 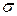-алгеброй, если аксиома А2 выполняется для счетного числа подмножеств.

Произвольное подмножество 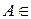A называется событием.

Событие, состоящее из всех элементарных исходов, называется достоверным событием.

Событие, не содержащее ни одного элементарного исхода, называется невозможным событием.

Событие 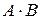называют произведением событий, если происходят оба события 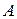и .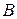

Событие 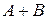называют суммой событий, если происходит хотя бы одно из событи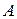й и .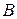

События 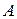и 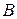называются несовместными, если их произведение является невозможным событием.

События 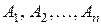образуют полную группу, если их сумма есть достоверное событие.

Два несовместных события, образующих полную группу, называются противоположными.

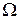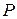Тройка ( , A, ) называется вероятностным пространством, где 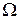– абстрактное множество, A – класс подмножеств 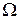, образующих 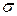-алгебру, 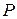– мера, определенная на классе A, со свойствами:

Р1. (аксиома неотрицательности) 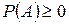, 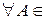A,

Р2. (аксиома нормированности) ,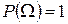

Р3. (расширенная аксиома сложения) Для любых попарно несовместных событий 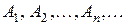справедливо равенство .

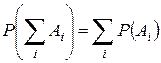Значение 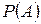называют вероятностью события .

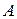Пусть 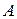и 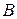– некоторые события, причем 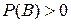. Условной вероятностью события 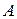при условии 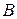(обозначается 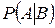) называется вероятность события 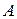, найденная при условии, что событие 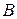произошло. Эта вероятность находится по формуле .

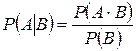Теорема умножения вероятностей: .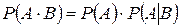

Одним из основных практических приложений понятия условной вероятности являются формулы полной вероятности и Байеса.

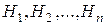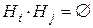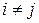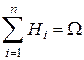Пусть события образуют полную группу попарно несовместных событий, т.е. ( ) и . События 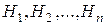назовем гипотезами. Относительно гипотез известны априорные (доопытные) вероятности .

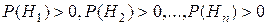Предположим, событие 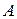может произойти только с одним из событий 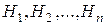и нам известны условные вероятности P(A| 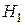), P(A| 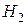),…, P(A| 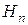). Тогда безусловная вероятность 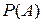вычисляется по формуле полной вероятности:

| .

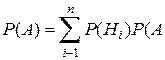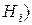Если в результате опыта произошло событие 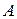, то прежние, априорные вероятности гипотез 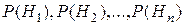должны быть заменены на новые, апостериорные (послеопытные) вероятности 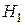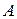P( | ), P( 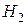| 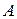),…, P( 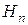| 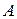), которые вычисляются по формуле Байеса:

P( | ) .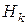

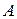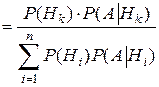Случайные величины

Скалярную функцию 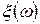, заданную на пространстве элементарных исходов 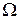, называют случайной величиной, если для любого 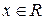множество элементарных исходов 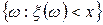является событием.

Для исследования вероятностных свойств случайной величины необходимо знать правило, позволяющее находить вероятность того, что случайная величина примет значение из подмножества ее значений. Любое такое правило называют законом распределения вероятностей.

Общим законом распределения, присущим всем случайным величинам, является функция распределения.

Функцией распределения случайной величины 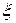называют функцию .

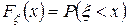Функция распределения обладает свойствами:

F1. Функция распределения любой случайной величины – неубывающая функция.

F2. Функция распределения непрерывна слева.

F3. , .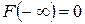

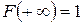4. .

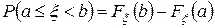5. .

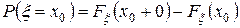Теорема. Функция распределения однозначно определяет распределение случайной величины.

Случайная величина 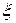называется дискретной, если она принимает не более чем счетное число значений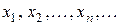

Распределение дискретной случайной величины удобно задавать соответствием между ее возможными значениями 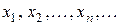и вероятностями 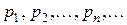, с которыми эти значения принимаются.

Функция распределения дискретной случайной величины имеет вид .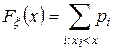

Случайная величина 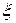называется непрерывной, если существует функция 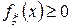, интегрируемая на всей числовой оси 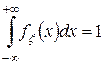, такая что функция распределения случайной величины представима в виде сходящегося несобственного интеграла 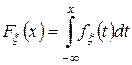. Функция 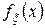называется плотностью распределения вероятностей.

Дискретная случайная величина 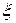распределена по закону Бернулли с параметром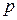 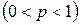, если она принимает значение 0 с вероятностью 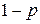и значение 1 с вероятностью .

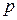Дискретная случайная величина 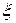распределена по биномиальному закону с параметрами и 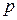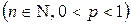, если она принимает значения 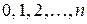с вероятностями .

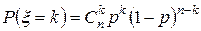Дискретная случайная величина 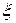распределена по закону Пуассона с параметром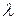 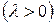, если она принимает целые неотрицательные значения с вероятностями .

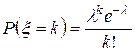Дискретная случайная величина 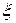распределена по геометрическому закону с параметром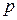 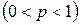, если она принимает натуральные значения с вероятностями .

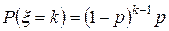Непрерывная случайная величина 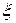имеет равномерное на 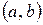распределение, если ее плотность распределения вероятностей имеет вид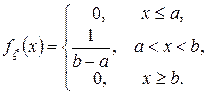

Непрерывная случайная величина 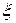распределена по нормальному закону с параметрами распределения 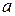и 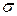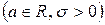, если ее плотность распределения вероятностей имеет вид .

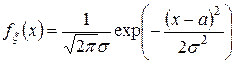Нормальное распределение с параметрам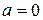и и 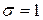называется стандартным нормальным распределением.

Непрерывная случайная величина 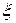распределена по экспоненциальному (показательному) закону, если ее плотность распределения вероятностей имеет вид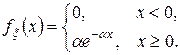

Основные числовые характеристики случайных величин

При решении многих задач нет необходимости находить закон распределения случайных величин, достаточно характеризовать их некоторыми неслучайными числами. Такие числа называют числовыми характеристиками.

Математическим ожиданием дискретной случайной величины 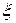называют неслучайное число 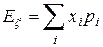. При этом, если множество значений случайной величины счетное предполагается, что ряд 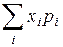сходится абсолютно. В противном случае говорят, что мат. ожидание не существует. Математическим ожиданием непрерывной случайной величины 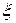называют неслучайное число 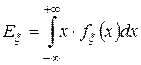. При этом предполагается, что 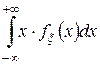сходится абсолютно.

Математическое ожидание является идеализированным средним значением случайной величины.

Свойства математического ожидания:

1. 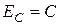, где .

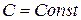2. , .

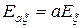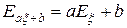3. 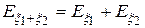, есл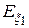и и 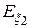существуют.

4. Если случайные величины 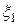и 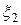независимы, то .

Для характеристики разброса возможных значений случайной величины относительно своего среднего значения служит дисперсия.

Дисперсией случайной величины 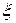называют математическое ожидание квадрата отклонения случайной величины от ее среднего значения .

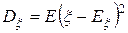Свойства дисперсии:

1. 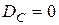, где .

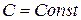2. , .

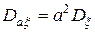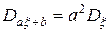3. .

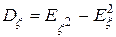Если случайные величины 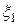и 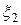независимы, то .

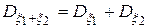Средним квадратическим отклонением случайной величины 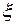называется число 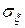, определяемое равенством 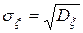. Величина 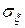неотрицательна и имеет ту же размерность, что и случайная величина .

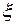Числовые характеристики важнейших распределений представлены в приложении 5.

Предельные теоремы теории вероятностей

Пусть 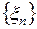– последовательность независимых одинаково распределенных случайных величин с конечным математическим ожиданием и дисперсией 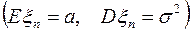. Обозначим через 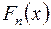функцию распределения нормированной суммы 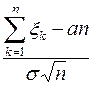, т.е.

.

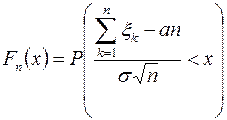Обозначим через 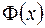функцию распределения стандартного нормального закона, т.е.

.

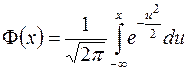Теорема (Центральная предельная теорема). Пусть 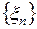– последовательность независимых одинаково распределенных случайных величин с конечным математическим ожиданием и дисперсией 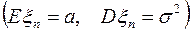. Тогда

.

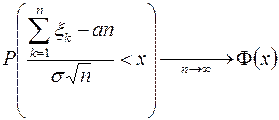Нормальный закон имеет важное значение на практике, поскольку, как правило, всегда встречается в ситуациях, когда случайная величина определяется большим количеством независимых случайных факторов, ни один из которых при этом не оказывает решающего влияния.

Функция 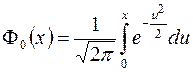называется функцией Лапласа.

Свойства функции Лапласа:

1. .

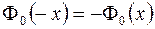2. .

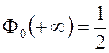3. .

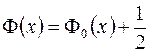4. Для .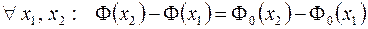

Следствием из центральной предельной теоремы являются интегральная и локальная теоремы Муавра-Лапласа.

Рассмотрим схему Бернулли, состоящую из 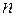независимых испытаний с вероятностью «успеха» 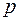. Обозначим через 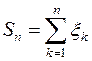– число успехов в схеме Бернулли, при этом случайные величины 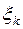независимы и одинаково распределены по закону Бернулли с параметром 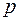, их числовые характеристики 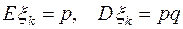. Тогда согласно центральной предельной теореме нормированная сумма 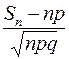сходится по распределению к стандартному нормальному распределению при .

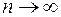Теорема (интегральная теорема Муавра-Лапласа). При достаточно большом 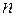вероятность того, что число успехов в схеме Бернулли будет не менее 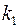и не более 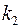, приближенно равна

,

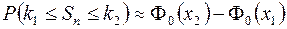где , .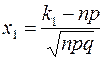

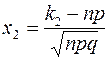Теорема (локальная теорема Муавра-Лапласа). При достаточно большом 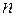вероятность того, что число успехов в схеме Бернулли будет 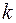, приближенно равна

,

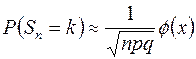где 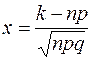, 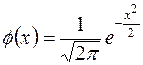– плотность распределения стандартного нормального закона.

Пусть вероятность успеха 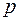является функцией от 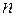, т.е. .

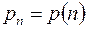Теорема Пуассона. Пусть 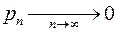, так что 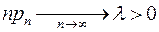, тогда при достаточно большом 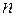вероятность того, что число успехов в схеме Бернулли будет 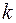, приближенно равна

.
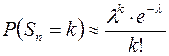