Построение решений в спектральной форме
Принимаем за основу соотношение (42), характеризующее решение уравнения  из экстремального класса
из экстремального класса  . Выберем в качестве функции
. Выберем в качестве функции 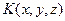 нулевое приближение к исходной модели среды. Тогда
нулевое приближение к исходной модели среды. Тогда  представляет собой спектр мощности нулевого приближения. Критерий оптимальности
представляет собой спектр мощности нулевого приближения. Критерий оптимальности  в содержательной форме имеет вид:
в содержательной форме имеет вид:


 (7.48)
(7.48)
Здесь  - функция, соответствующая оператору свертки
- функция, соответствующая оператору свертки  . Представляется, что минимизация этого выражения соответствует максимизации с обратной в смысле алгебры сверток функцией:
. Представляется, что минимизация этого выражения соответствует максимизации с обратной в смысле алгебры сверток функцией:
 (7.49)
(7.49)
Но в силу симметрии  , следующей из того, что
, следующей из того, что  критерий (49) и (48) ассоциируется с требованием максимизации функции взаимной корреляции между искомым распределением плотности и заданным нулевым приближением (точнее его автокорреляционной функцией). Далее следует разработать устойчивый способ вычисления значения этого неограниченного оператора на заданном поле
критерий (49) и (48) ассоциируется с требованием максимизации функции взаимной корреляции между искомым распределением плотности и заданным нулевым приближением (точнее его автокорреляционной функцией). Далее следует разработать устойчивый способ вычисления значения этого неограниченного оператора на заданном поле 
Для устойчивого вычисления значения (42):
 (7.42)
(7.42)
должны быть использованы методы регуляризации, рассмотренные ранее в гл. 4. Один конкретный способ вычислений излагается ниже.
Спектры функций, входящих в (42), заменяются коэффициентами ДПФ (дискретное преобразование Фурье), вычисляемыми по формуле:
 (7.50)
(7.50)
Обратное преобразование задается соотношением:
 (7.51)
(7.51)
Здесь:  ,
,
 - количество узлов сетки в направлении оси
- количество узлов сетки в направлении оси 
 - количество узлов сетки в направлении оси
- количество узлов сетки в направлении оси 

Замена преобразования Фурье на ДПФ приводит к погрешностям. С целью уменьшения их влияния вместо вычисления1:

осуществляется расчет ДПФ от гравитационного эффекта  соответствующего распределению плотности
соответствующего распределению плотности  . Обозначим
. Обозначим 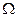 - область отличных от нуля коэффициентов Фурье функций
- область отличных от нуля коэффициентов Фурье функций 

 предполагая, что коэффициенты при всех
предполагая, что коэффициенты при всех  равны нулю. Кроме того, будем считать, что
равны нулю. Кроме того, будем считать, что  имеет нулевыми коэффициентами все те, которые отличны от нуля и
имеет нулевыми коэффициентами все те, которые отличны от нуля и  Пусть:
Пусть:


 (7.52)
(7.52)
Или:
 (7.53)
(7.53)
Норму функций  и
и  определим равенствами:
определим равенствами:
 (7.54)
(7.54)
Оператор (52) рассмотрим как отображение  в
в  с нормами (54). Тем самым определится и норма оператора (52). Далее для краткости письма там, где это не приводит к недоразумениям, отождествляем
с нормами (54). Тем самым определится и норма оператора (52). Далее для краткости письма там, где это не приводит к недоразумениям, отождествляем  и
и  с
с  соответственно.
соответственно.
Имеем:
 (7.55)
(7.55)
Следовательно, норма оператора (52) ограничена величиной  . Вычислим, на сколько в норме (54) отличаются
. Вычислим, на сколько в норме (54) отличаются  и
и  .
.
 Тогда после деления на
Тогда после деления на  :
:
 (7.56)
(7.56)
следовательно, выбор 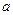 из условия:
из условия:
 . (7.57)
. (7.57)
обеспечивает согласованность погрешности, с которой задано  (в смысле (54)), и величины параметра регуляризации
(в смысле (54)), и величины параметра регуляризации 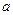 .
.
При выборе параметра 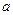 следует учитывать два, в общем, противоречивых обстоятельства. С одной стороны, увеличение
следует учитывать два, в общем, противоречивых обстоятельства. С одной стороны, увеличение 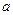 приводит к повышению устойчивости решения (см. (55)). Оценка для
приводит к повышению устойчивости решения (см. (55)). Оценка для 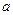 из (57), обеспечивая заданную величину невязки, может не обеспечивать требуемую устойчивость, и наоборот. Фактически это означает лишь то, что регуляризующее слагаемое в знаменателе
из (57), обеспечивая заданную величину невязки, может не обеспечивать требуемую устойчивость, и наоборот. Фактически это означает лишь то, что регуляризующее слагаемое в знаменателе  выбрано не лучшим образом. Для обеспечения заданного типа устойчивости и минимизации невязки воспользуемся итерационным процессом:
выбрано не лучшим образом. Для обеспечения заданного типа устойчивости и минимизации невязки воспользуемся итерационным процессом:
 (7.58)
(7.58)
где  - рассчитанный дискретный спектр гравитационного поля от
- рассчитанный дискретный спектр гравитационного поля от  .
.
Пусть  Тогда итерационный процесс (58) сходится к элементу из
Тогда итерационный процесс (58) сходится к элементу из  с гравитационным эффектом, равным
с гравитационным эффектом, равным  , причем:
, причем:
 (7.59)
(7.59)
 (7.60)
(7.60)
Сходимость процесса (58) к постулируемому решению следует из оценок (59) и (60). Их и следует доказать. Из (55) имеем:
 (7.61)
(7.61)
Из (56) следует:
 . (7.62)
. (7.62)
Подставляя последнее выражение в (61) получаем (59). Результат доказан.
