Указания к проведению и порядок работы

Введение

Сегодня

предприятиям надо обеспечить соответствие выпускаемой продукции требованиям международных стандартов ISO, что невозможно без использования CALS-технологий. В настоящее время в РФ всё больше внимания уделяется интеграции информационных технологий практически во все отрасли машиностроения, идёт активное внедрение совершенно новых автоматизированных средств информационной поддержки изделий на всех этапах жизненного цикла. Особое внимание уделяется новым перспективным направлениям разработки и управления технологическими процессами (ТП) механообработки с использованием нейросетевого моделирования.

Ниже представлена сравнительная таблица обзора характеристик методов управления с относительной оценкой основных параметров (Таблица 1).

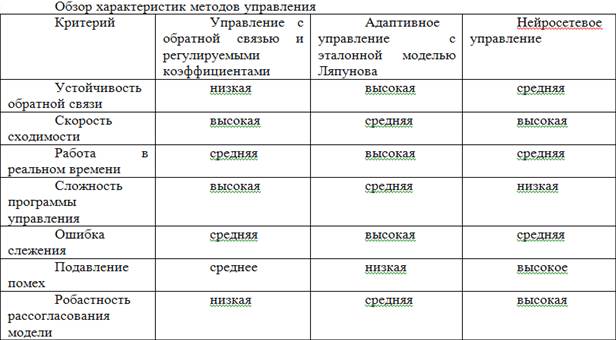
В последние годы резко повысился интерес к таким научным направлениям как идентификация, нейроуправление, нейропрогнозирование с использованием нечеткой логики.

Цели и задачи работы.

В технике довольно часто возникают ситуации, когда невозможно получить исчерпывающую информацию для построения точной математической модели объекта управления. К неточной информации можно отнести большое разнообразие возмущающих воздействий, изменяемых в процессе работы станка; изменение таких параметров окружающей среды как температура, трение в исполнительных механизмах и т.д.

Нейроуправление значительно улучшает характеристики технологического оборудования. Системы управления станками с ЧПУ с нечеткой логикой обеспечивают более высокие показатели качества, обладают лучшими статическими и динамическими характеристиками и поэтому являются перспективным направлением при создании новых современных технологий в области нейроуправления.

Преимуществами НС перед традиционными системами управления является:

1. НС могут обучаться любым функциям, важен только объем предоставленных данных и выбор правильной нейронной модели. Таким образом НС позволяют избежать использования сложного математического аппарата;

2. Использование нелинейных функций активации в нейронных сетях позволяет реализовать задачи с существенными нелинейностями;

3. НС являются самообучаемыми системами. Это означает возможность осуществлять управление в условиях существенных нелинейностей;

4. Высокая степень параллельности НС обеспечивает высокую производительность вычислений;

5. Архитектура параллельной обработки позволяет НС функционировать даже при повреждении отдельных элементов сети.

Из этого следует, что нейронные сети имеют большие перспективы в области управления сложным технологическим оборудованием.

Искусственный нейрон является составной частью нейронной сети. На рис.1 показана его структура. Он состоит из элементов трех ти­пов: умножителей (синапсов), сумматора и нелинейного преобра­зователя.

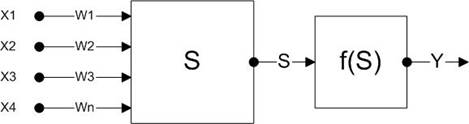
Рис. 1. Структура искусственного нейрона

Нейрон в целом реализует скалярную функцию векторного аргумента. Математическая модель нейрона:

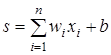(5)

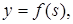(6)

где 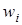, - вес (weight) синапса, 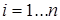; 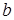- значение смещения (bias); s - результат суммирования (sum); x, - компонент входного вектора (входной сигнал), i = 1...п; у - выходной сигнал нейрона; n - число входов нейрона; f - нелинейное преобразование (функ­ция активации).

Указания к проведению и порядок работы.

На основании полученных данных обработки партии гладкого вала в течении смены составить таблицу данных («банк данных»), указать требуемые параметры для формирования пакета входных данных НС.

Пример:

Пластинка: CNMG 120408-M3 ТР3000

Резец: POLNR 2525M12

N=630 об/мин

Подача 0,3 мм/об.

Таблица результатов измерений

Время измерений	Результаты измерений, мкм
№1	№2	№3	№4	№5	№6
1ч	0,25	0,12	0,19	0,24	0,16	0,17
0,14	0,08	0,22	0,18	0,10	0,15
2ч	0,16	0,27	0,34	0,18	0,27	0,14
0,11	0,09	0,36	0,12	0,18	0,29
3ч	0,08	0,01	0,11	0,20	0,23	0,12
0,34	0,31	0,47	0,42	0,33	0,27
4ч	0,26	0,41	0,57	0,29	0,32	0,24
0,24	0,35	0,38	0,27	0,16	0,14
5ч	0,35	0,27	0,21	0,30	0,15	0,09
0,11	0,19	0,27	0,21	0,08	0,17
6ч	0,54	0,38	0,42	0,49	0,31	0,24
0,45	0,48	0,31	0,26	0,20	0,32

Рис. 2. Таблица результатов эксперимента (относительные отклонения)

Для оценки числа нейронов в многослойной сети можно воспользоваться формулой:

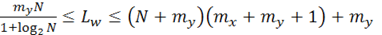где 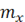- размерность входного сигнала, 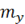-размерность выходного сигнала, N-числообучающей выборки, Lw-необходимое число синаптических весов.

Оценив необходимое число весов, можно рассчитать число нейронов в скрытых слоях для двухслойной сети:

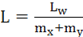Принимаем: среднеквадратическое значение погрешности

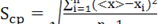где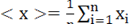

среднее арифметическое значение истинного результата измерений.

Подставляя вместо <x>≡ 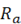, получаем для распространённого случая двух входов на нейрон:

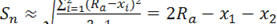При использовании НС за счёт множества циклов обучения можем принять построение результирующих точек условно равным:

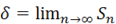В качестве функции активации 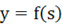можем принять такую величину, при которой заданная погрешность будет выполнять роль пороговой ошибки обучения. При этом при увеличении ошибки (погрешности) будет сокращаться число циклов обучение и, как следствие понижаться требования к базе измерений обработанных деталей для заполнения таблицы обучения нейронной сети. При уменьшении ошибки (погрешности) произойдёт повышение точности сети, но за счёт сокращения быстродействия и повышения чувствительности к «зашумлённости» результатов базовых измерений вследствие случайных погрешностей; при этом

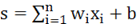уравнение активации нейрона в сети, где 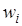, - вес синапса, 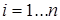; 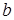- значение смещения; s - результат суммирования; 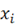- входной сигнал, i = 1...n; n - число входов нейрона; f - функ­ция активации.

Выводы

На основании полученных данных можно утверждать о возможности применения прикладного пакета нейросетевого моделирования для решения задачи коррекции управляющей программы в процессе обработки.

Параметры, которые будет использовать сеть в качестве входных данных, а также построить теоретическую модель функции активации нейрона с указанием возможного порога срабатывания и выходные данные сети: а именно, по какому образцу возможно «обучение» сети и какие параметры можем принять в качестве ошибки обучения.

Лабораторная работа №2.

«Модели оптимизации в многофакторных экспериментах».

Введение

Научное исследование – это такое систематическое и целенаправленное изучение объектов, в котором используются методы и средства науки и которое завершается формулированием знаний об изучаемых объектах (гипотез, теорий, законов, методов проведения экспериментов, методов расчета и др.).

Объектом научного исследования является материальная или идеальная система.

Предметом научного исследования является структура системы, закономерности взаимодействия элементов внутри системы или вне ее, закономерности развития и т.п.

Цель научных исследований (объектов, процессов или явлений) – всестороннее достоверное получение, изучение и формулирование новых знаний, которые будут использованы для решения технических, экономических, социальных, гуманитарных и других задач.

При разработке технологических процессов используют методы структурной и параметрической оптимизации по разным критериям, которые можно объединить в две группы:

1) экономические критерии (минимальная технологическая себестоимость, наименьшие приведенные затраты, наибольшая прибыль и др.);

2) критерии технического уровня (максимальный уровень автоматизации, максимальная производительность, наибольший коэффициент использования материалов, наибольший коэффициент загрузки оборудования и др.).

Структура элементов таких моделей описывается ориентированным графиком, не имеющим замкнутых циклов. Модель содержит большое число вариантов техпроцесса, в которых строго сохраняется порядок следования элементов, соответствующий технологическим операциям.

Цели и задачи работы.

Основной целью экстремальных экспериментов является нахождение наилучших (оптимальных) решений по выбранному критерию (параметру оптимизации). Для этого задается некоторый критерий оптимизации в виде целевой функции y, зависящий от управляемых параметров (факторов варьирования)

.

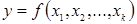Задача оптимизации сводится к отыскиванию таких значений параметров 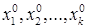, при которых целевая функция достигает экстремума (максимума или минимума). Будем считать оптимальным максимальное значение параметра оптимизации. Зависимость 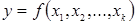образует некоторую поверхность в (k+1) мерном пространстве 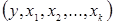, которую называют поверхностью отклика, а значение y в точках факторного пространства – откликом.

Если бы поверхность отклика можно было описать в аналитической форме в виде приведенной функции, то координаты точки экстремума 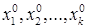можно найти, решив систему дифференциальных уравнений вида

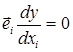, где i = 1,2,…,k.

Решением системы является экстремальная точка (или «стационарная точка»), в которой градиент функции у обращается в нуль

,

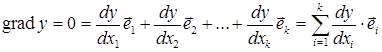где – направляющий вектор координатной оси x_i.

Однако в большинстве случаев экспериментальных исследований аналитическая функция «у» неизвестна. Исследователь имеет возможность только экспериментально получить значение отклика при некоторой комбинации варьируемых факторов 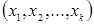. Полученное экспериментально значение отклика y_э всегда содержит случайную ошибку, т.е. оно будет отличаться от истинного значения y_i на величину случайной ошибки опыта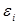

.

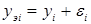Таким образом, задача оптимизации может быть решена двумя методами.

1) Каким-либо способом строиться математическая модель и задача решается аналитически или численным способом.

2) Поиск экстремальной («стационарной») точки в факторном пространстве 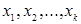проводится экспериментально. При этом осуществляется локальное изучение поверхности отклика по результатам ряда экспериментов, специально спланированных вблизи выбранной точки. Экспериментальное значение отклика находится путем многократной исследовательской процедуры изучения поверхности отклика и продвижения в факторном пространстве. Для движения к оптимуму широко используется шаговый принцип, при котором строится математическая модель поверхности отклика и движение по факторному пространству осуществляется шагами с периодической оценкой правильности направления движения. Предполагается, что поверхность отклика гладкая, непрерывная и на ней имеется единственный оптимум. В этом случае, проводя ряд экспериментов, можно установить направление дальнейшего движения к оптимуму.

Известны несколько методов экспериментального поиска оптимума, различающихся способом определения направления движения и организацией самого движения.

В лабораторной работе рассмотрим наиболее широко применяемые экспериментальные методы и сравним результаты применённых моделей оптимизации.