Распределительные задачи

Распределение рабочих по сменам и участкам. Определить явочный состав работающих каждого из трех участков цеха при условии, что суточная выработка продукции будет максимальной (режим работы на предприятии – трехсменный). При этом требуется, чтобы в соответствии с имеющимся объемом работ число работающих первого участка не превышало 100 чел., второго – 160 чел, а общее число работающих было не более 400 чел. Известна средняя суточная производительность труда работающих соответственно по каждому из участков: 70, 60, 50 шт. По условиям безопасности труда в цехе необходима хорошая вентиляция. На одного работающего каждого участка должно приходиться не менее 4,5; 6; 9 м³/мин воздуха. Мощность цеховой вентиляционной установки 800 м³/мин.

Математическая модель задачи.

Обозначим через x_ij– количество работающих на i-м участке в j-ю смену.

Функция цели (максимизация выработки продукции):

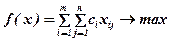
ограничения по числу работающих на участках

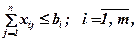
ограничение на общее количество рабочих в цехе

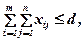
ограничения, связанные с требованиями вентиляции

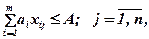
условие неотрицательности решения

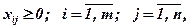
где с_j – средняя выработка на i-м участке (шт./чел.); b_i – максимальное общее количество работников на i-м участке с учетом трехсменного режима работы; d – максимально возможное общее число работающих в цехе во всех сменах; a_i – потребность в воздухе на i-м участке на каждого человека; А – мощность вентиляционной системы цеха; i – номер участка; m – число участков; j – номер смены; n – число рабочих смен в цехе.

Подставим исходные данные в модель

max f(x) = 70x₁₁+70x₁₂+70x₁₃+60x₂₁+60x₂₂+60x₂₃+

+50x₃₁+50x₃₂+50x₃₃

x₁₁+x₁₂+x₁₃ ≤ 100

x₂₁+x₂₂+x₂₃ ≤ 160

x₁₁+x₁₂+x₁₃+ x₂₁+x₂₂+x₂₃+x₃₁+x₃₂+x₃₃ ≤ 400

7,5x₁₁+6x₂₁+9x₃₁ ≤ 800

7,5x₁₂+6x₂₂+9x₃₂ ≤ 800

7,5x₁₃+6x₂₃+9x₃₃ ≤ 800

x_ij ≥ 0; i = 1, 2, 3; j = 1, 2, 3.

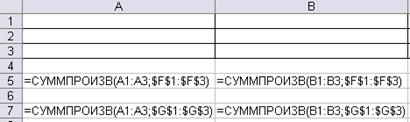
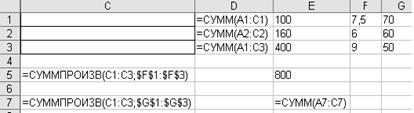
Рис. 9. Ввод модели в Excel

При вводе модели и исходных данных в Excel (рис. 9) используем функцию из категории Математические - =СУММПРОИЗВ. Массив ячеек А1:С3 отведём под изменяемые ячейки для размещения неизвестных переменных x_ij. Функция цели введена в ячейку Е7, а её составляющие – в ячейки А7:С7. Формулы ограничений по численности работников введены в ячейки D1:D3, а по мощности вентиляционной системы жизнеобеспечения – в ячейки А5:С5.

В меню Сервис выбираем программу Поиск решения (при её отсутствии - в меню Сервис выбрать Надстройки и установить флажок у программы Поиск решения).

В программе Поиск решения указать (рис. 10) адрес ячейки с целевой функцией, направление поиска экстремума функции цели, адреса изменяемых ячеек с искомыми переменными. После нажатия кнопки Параметры установить флажки: Линейная модель и Неотрицательные значения.

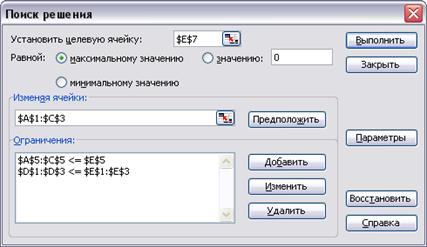
Рис. 10. Ввод модели в программу Поиск решения

Если задача имеет множество решений, то многократный запуск программы Поиск решения позволит выявить эти решения.

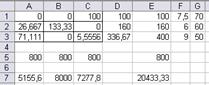
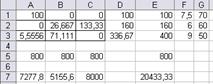
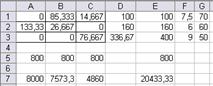
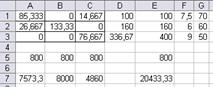
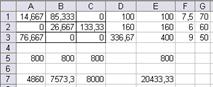
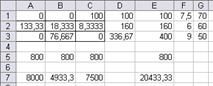
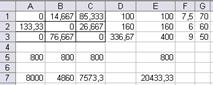
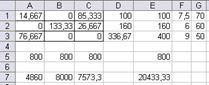
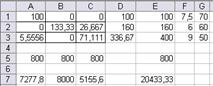
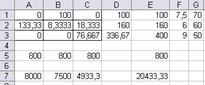
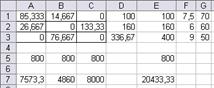
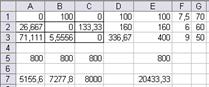
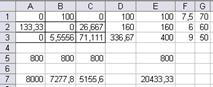
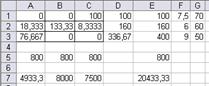
Рис. 11а. Множество вариантов оптимального

распределения работников

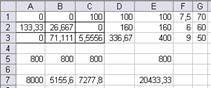
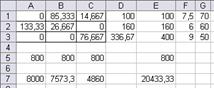
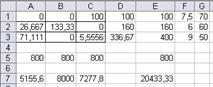
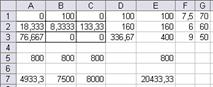
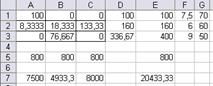
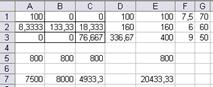
Рис. 11б. Множество вариантов оптимального

распределения работников

Решение задачи симплекс-методом (число переменных = 15, число ограничений = 6):

x₁ x₂ x₃ x₄ x₅ x₆ x₇ x₈ x₉ x₁₀ x₁₁x₁₂ x₁₃x₁₄ x₁₅

1 1 1 0 0 0 0 0 0 1 0 0 0 0 0 100

0 0 0 1 1 1 0 0 0 0 1 0 0 0 0 160

1 1 1 1 1 1 1 1 1 0 0 1 0 0 0 400

7,5 0 0 6 0 0 9 0 0 0 0 0 1 0 0 800

0 7,5 0 0 6 0 0 9 0 0 0 0 0 1 0 800

0 0 7,5 0 0 6 0 0 9 0 0 0 0 0 1 800

-70 -70 -70 -60 -60 -60 -50 -50 -50 0 0 0 0 0 0

Решение: f(x) = -20433,33

x₍₁₁₎=x₁=14,67 x₍₁₃₎=x₃=85,33 x₍₂₂₎=x₅=133,33

x₍₂₃₎=x₆=26,67 x₍₃₁₎=x₇=76,67 x₁₂=63,33

Таблица распределения работников по сменам и участкам

	1 смена	2 смена	3 смена
I участок	14,67		85,33
II участок		133,33	26,67
III участок	76,67

Количество свободных рабочих мест суммарно по трем сменам – 63,33. Общий выпуск продукции в сутки 20433,3 шт.

Модель производства с запасами

Фирма переводит свой завод на производство новых изделий, которые планируется выпускать в течение четырёх месяцев. Оценки спроса на изделия в каждый из этих месяцев приведены в таблице:

Месяц поставки изделия
Спрос (штук)

В каждый месяц спрос можно удовлетворить за счёт;

- избытка изделий, произведённых в предшествующие месяцы;

- изделий, произведённых в текущем месяце;

- изделий, произведённых в последующие месяцы для погашения невыполненных ранее заказов.

Затраты на изготовление одного изделия составляют 4 ден.ед. Изделие, произведённое, но не поставленное потребителю в текущем месяце, влечёт за собой дополнительные издержки на хранение в размере 0,5 ден.ед. за каждый месяц хранения. Изделие, выпускаемое в счёт невыполненных заказов, облагается штрафом в размере 2 ден.ед. за каждый месяц недопоставки.

Объем производства меняется от месяца к месяцу по внутризаводским причинам. В рассматриваемые 4 месяца планируется следующая программа выпуска изделий:

Месяц производства изделия
Выпуск (штук)

Требуется уточнить (доопределить) эту программу таким образом, чтобы она обеспечивала минимальные издержки, обусловленные несогласованностью спроса и предложения (дисбалансом).

Задачи такого типа в исследовании операций известны как транспортные задачи. Это обусловлено тем, что чаще всего такие задачи связаны с оптимизацией процессов перевозок. Вместе с тем к этому типу сводится рассматриваемая задача и многие другие, не имеющие непосредственного отношения к транспорту. Специфика этих задач заключается в использовании таблицы-матрицы, строки и столбцы которой определяют факторы дисбаланса – спрос и предложение, место производства и потребления продукции и т.п.

Математическая формулировка задачи. Пусть i определяет месяц производства изделия, а, j - месяц поставки. Примем в качестве переменных x_ij – количество изделий, произведённых в i-й месяц и поставленных в j-й. (Эти переменные будут размещаться в изменяемых ячейках.) a_i – программа выпуска изделий в i-м месяце, b_j – спрос в j-м месяце, с_ij - затраты на продукцию, производимую в i-м месяце и потребляемую в j-м месяце.

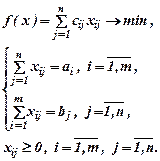
Определим матрицу объёма производства, а также стоимостей производства и хранения изделий (в ден.ед):

Месяц производства (i)	Месяц потребления (j)	Программа выпуска изделий (шт)
	X11 4	X12 4,5	X13 5	X14 5,5
	X21 6	X22 4	X23 4,5	X24 5
	X31 8	X32 6	X33 4	X34 4,5
	X41 10	X42 8	X43 6	X44 4
Спрос (шт)

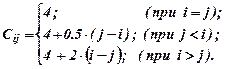
Ограничения:

предложение (объём производства):

х₁₁ + х₁₂ + х₁₃ + х₁₄ = 50;

х₂₁ + х₂₂ + х₂₃ + х₂₄ = 180;

х₃₁ + х₃₂ + х₃₃ + х₃₄ = 280;

х₄₁ + х₄₂ + х₄₃ + х₄₄ = 270;

спрос:

х₁₁ + х₂₁ + х₃₁ + х₄₁ = 100;

х₁₂ + х₂₂ + х₃₂ + х₄₂ = 200;

х₁₃ + х₂₃ + х₃₃ + х₄₃ = 180;

х₁₄ + х₂₄ + х₃₄ + х₄₁ = 300.

Целевая функция:

Z = 4х₁₁ + 4,5х₁₂ + 5х₁₃ + 5,5х₁₄ + 6х₂₁ + 4х₂₂ + 4,5х₂₃ + 5х₂₄ +

+ 8х₃₁ + 6х₃₂ + 4х₃₃ + 4,5х₃₄ + 10х₄₁ + 8х₄₂ + 6х₄₃ + 4х₄₄ → min;

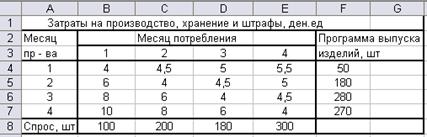
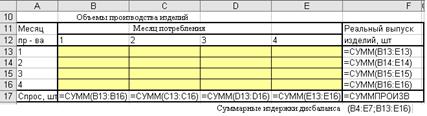
Рис. 12. Ввод модели в Excel

Как изменится найденное решение, если издержки на хранение будут больше штрафа, равны штрафу?