Произведем расчет критериев надежности системы по полученным формулам
Для заданных значений t = 8760 ч и 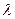 = 8∙10-5 1/ч
= 8∙10-5 1/ч
Pсист = 0,33663038
mt( 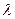 =8∙10-5) = 7,708*103 ч.
=8∙10-5) = 7,708*103 ч.
Система с частично нагруженным резервом
 |
Рис. 5. Схема надежности невосстанавливаемой резервированной системы с дробной кратностью с частично нагруженным резервом
Основными являются элементы 1 – 4, резервными – 5 - 6.
Т.к. система невосстанавливаемая, отказавший элемент не может быть восстановлен. Элементы 5, 6 находятся в резерве и работают в облегченном режиме. При отказе основного элемента он заменяется на резервный; если исправных резервных элементов не остается, система выходит из строя.

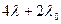
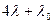

0 1 2 3
Рис. 6. Граф состояний системы
Найдем критерии надежности системы методом дифференциальных уравнений.
Система дифференциальных уравнений, соответствующая графу состояний системы, имеет вид:
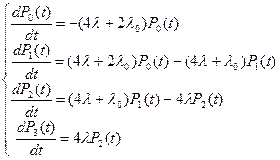
Нормировочное условие: 
Начальные условия для системы дифференциальных уравнений:
P0(0)=1
P1(0)=0
P2(0)=0
P3(0)=0
При расчете методом дифференциальных уравнений, после применения прямого преобразования Лапласа при начальных условиях система принимает вид:
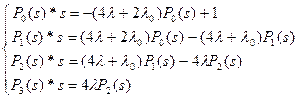
Решая систему уравнений, получим:
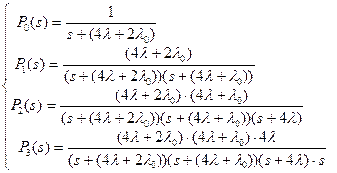
После применения обратного преобразования Лапласа:
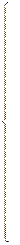 |
 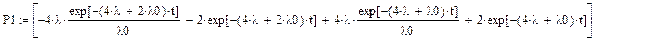 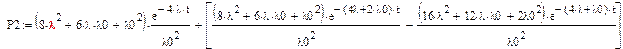 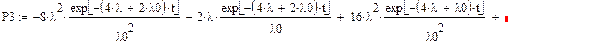 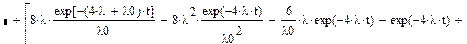 |
Вероятность безотказной работы системы равна:
Pсист = 1-P3(t) =
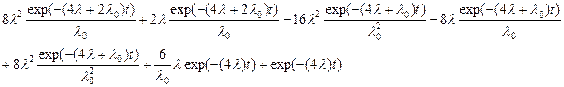 |
Среднее время безотказной работы:
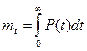 =
= 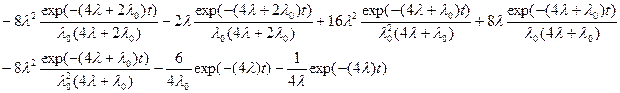
Найдем критерии надежности данной системы методом интегральных уравнений.
Рассмотрим события, которые могут произойти с системой на отрезке времени t:
1.Цепь отработала успешно все время t с интенсивностью отказов 4λ+2λ0.Ни один из элементов не отказал.
Вероятность успешной работы:
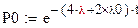
2. Цепь отработала без отказа время τ с интенсивностью 4λ+2λ0, после чего продолжала работать оставшееся время t-τ без отказа с интенсивностью отказов 4λ+λ0.
Вероятность отказа системы во время τ:
 (4λ+2λ0)
(4λ+2λ0) 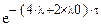
Вероятность успешной работы системы уже из 2 элементов оставшееся время:
P1(t-τ)= 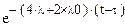
Вероятность успешной работы:
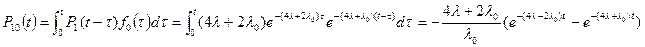
3. Цепь отработала без отказа время τ с интенсивностью отказов 4λ+2λ0, после чего продолжала работать время τ1-τ без отказа с интенсивностью отказов 4λ+λ0.В момент времени τ1 система отказывает повторно и работает оставшееся время t- τ1 без отказов с интенсивностью отказов 4λ.
Вероятность отказа системы во время τ1:
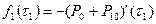
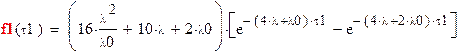
Вероятность успешной работы системы уже из 1 элемента оставшееся время:
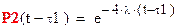
Вероятность успешной работы:
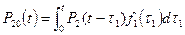
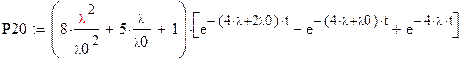
Вероятность успешной работы системы в целом:
P(t)=P0(t)+P10(t)+P20(t)
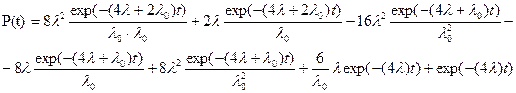
В результате мы получили те же результаты что и методом дифференциальных уравнений.
Произведем расчет критериев надежности системы по полученным формулам.
Для заданных значений t = 8760 ч и 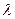 = 8∙10-5 1/ч
= 8∙10-5 1/ч
Pсист = 0,37877057
mt( 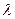 =8∙10-5) = 87,278*102 ч.
=8∙10-5) = 87,278*102 ч.
