Результаты промежуточных вычислений должны иметь 1-2 запасных знака, которые должны быть затем отброшены
Теория погрешностей. Приближенные величины.
Пусть 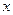 - точное значение некоторой величины и
- точное значение некоторой величины и 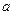 - приближенное значение этой величины.
- приближенное значение этой величины.
Определение. Разность 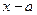 называется абсолютной погрешностью числа
называется абсолютной погрешностью числа 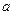 .
.
Определение. Выражение 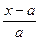 называется относительной погрешностью числа
называется относительной погрешностью числа 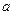 .
.
Для характеристики погрешности обычно указывают её границу.
Определение. Любое число 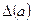 , удовлетворяющее неравенству
, удовлетворяющее неравенству 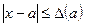 , называется границей абсолютной погрешности.
, называется границей абсолютной погрешности.
Определение. Любое число 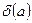 , удовлетворяющее неравенству
, удовлетворяющее неравенству 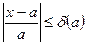 , называется границей относительной погрешности.
, называется границей относительной погрешности.
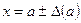 указывает на то, что число
указывает на то, что число 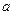 является приближенным значением числа
является приближенным значением числа 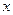 с границей абсолютной погрешности
с границей абсолютной погрешности 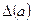 , т.е.
, т.е. 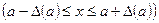 .
.
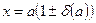 .
.
Виды погрешности:
1) погрешности, возникающие при неточности описания реального процесса (погрешность математической модели);
2) погрешности входных данных;
3) погрешности метода;
4) погрешности вычисления.
Погрешности 1) и 2) являются неустранимыми.
Значащие и верные цифры.
Пусть 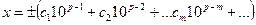 , где
, где 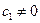 , и
, и
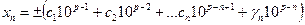 , где
, где
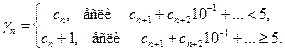
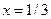
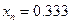
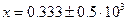
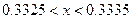
Определение. Значащими цифрами числа в его позиционной записи называются все цифры, начиная с первой ненулевой слева.
Определение. Значащую цифру называют верной, если абсолютная погрешность числа не превосходит единицы разряда, в котором стоит эта цифра.
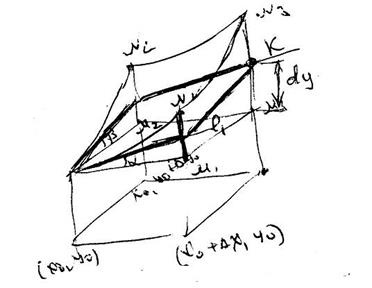
Погрешности вычислений.
Пусть 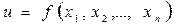 ,
, 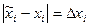
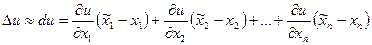
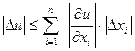
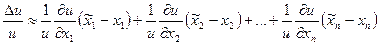
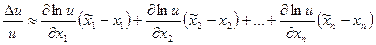
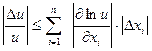
Погрешности арифметических действий.
Сложение и вычитание
Пусть 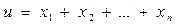 , тогда
, тогда
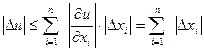
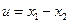
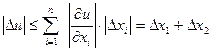
При сложении и вычитании абсолютные погрешности складываются.
Пусть теперь числа 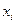 положительные и
положительные и 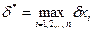 и
и
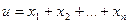 .
.
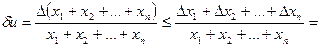
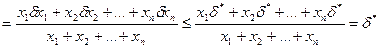 .
.
Относительная погрешность суммы 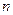 положительных чисел не превосходит максимума относительной погрешности слагаемых.
положительных чисел не превосходит максимума относительной погрешности слагаемых.
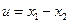
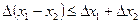
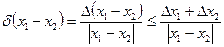
При 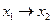 относительная погрешность разности
относительная погрешность разности 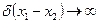 .
.
Умножение
Пусть 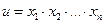 , тогда
, тогда
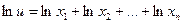
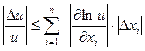
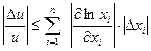
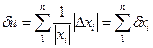
При умножении относительная погрешность не превосходит суммы относительных погрешностей сомножителей.
Деление
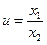
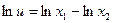
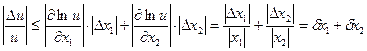
При делении относительная погрешность не превосходит суммы относительных погрешностей делимого и делителя.
Обратная задача теории погрешности.
Какой точности необходимо задать данные на вход, чтобы на выходе получить результат заданной точности?
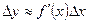 , откуда
, откуда 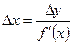 .
.
Принцип Крылова.
Приближенное число должно записываться так, чтобы все значащие цифры, кроме последней, были бы верными. При этом последняя отличалась бы не более чем на единицу этого разряда.
Правила.
При сложении и вычитании приближенных чисел в результате следует сохранять столько десятичных знаков (знаки после запятой), сколько их в приближенном данном с наименьшим количеством десятичных знаков.
При умножении и делении приближенных чисел следует сохранять столько значащих цифр, сколько их имеет приближенное число с наименьшим числом значащих цифр.
Результаты промежуточных вычислений должны иметь 1-2 запасных знака, которые должны быть затем отброшены.
