Экстремальные классы в задачах структурной гравиметрии (СГ)

Оператор прямой задачи гравиметрии для структурных задач имеет вид (2.4)

, (7.66)

что в операторной форме имеет вид .

Перепад плотности на границах может быть функцией горизонтальных координат.

Особое значение имеет случаи, когда поле задано на поверхности рельефа в той, либо иной, системе точек, образующей множество . Для того чтобы подчеркнуть эти обстоятельства и конечность области 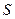- проекции на 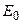носителя аномальные массы будем, по аналогии с (19), использовать операторное обозначение для (66):

(7.67)

Запись будем использовать в случае, когда поле задано всюду на 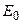( рельеф плоский, ), область 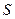конечна и регулярна, либо бесконечна и тогда границы выходят на асимптоты. В последнем случае асимптоты должны быть горизонтальными плоскостями, существенное отличие от которых поведения границ имеется только в конечной подобласти .

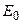Как для случая (66) , так и (18) следует учитывать при расчетах, что для принципиальной возможности сопоставления с наблюдаемой компонентой гравитационного поля должны быть учтены массы, расположенные вне постулированной области для случая (19), и имеющие проекцию своих источников на 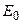, выходящую за 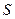. Для структурных задач это имеет особо важное значение. Здесь нельзя отождествлять интерпретируемую компоненту поля, которая укладывается в рамки модели задачи (67), и наблюдаемую, существенно от нее отличающуюся, прежде всего, за счет влияния того, что реальные границы имеют продолжение за 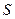. Именно для того, чтобы подчеркнуть это обстоятельство в (66) для интерпретируемой компоненты поля использована запись , а не подчеркивающая, что это приращение поля относительно иных источников. Выделенная компонента, ответственная за гравитационное влияние плотностных границ внутри области, ограниченной на поверхности наблюдений площадью 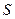. Это влияние называется влиянием боковых зон. Оно достаточно очевидно учитывается для двухмерного случая, но требует серьезных дополнительных предположений в трехмерном. При рассмотрении конкретных алгоритмов моделирования гравитационного поля для структурных задач следует особо внимательно отнестись к тому, как учитывается влияние боковых зон и особенно в трехмерном случае. Никакие надежды на то, что этот вопрос «сам собой решиться» за счет использования достаточно больших областей 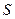неоправданны. Погрешности, связанные с не учетом влияния боковых зон велики, как при решении региональных, так зональных и локальных, задач.

Оператор (66) отображает систему из 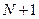плотностных границ , рассматриваемой как в некоторый элемент из функционального пространства на 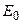. В качестве такого может выступать 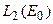с мерой 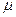, учитывающей способ задания поля . Это отображение является частным случаем и по этой причине наследует свойства оператора (18). Однако, в отличие от (18) является нелинейным.

Справедлив следующий результат.

есть множество первой категории в ;

Существует константа 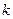такая, что .

Это очевидные следствия аналогичных результатов для (1).

Для характеристики экстремальных классов, соответствующих уравнению (66) воспользуемся результатами 5.6.1. и, в частности, соотношением (5.59) для решения задачи (5.58). Аналогом (5.58) будет:

(7.68)

где линейный замкнутый оператор, отображающий в себя. Операторы могут быть операторами свертки с некоторыми заданными функциями , либо операторами умножения на весовые функции. Содержательная запись этой задачи такова:

(7.69)

Здесь - нулевые приближения к изучаемым границам (см. также 5.1). Компоненты задачи схематично изображены на рис.7.3.

Рис.7.3 Модель задачи.

Для характеристики экстремального класса необходимо вычислить сопряженный к производной оператора . Производная (Фреше) оператора в «точке» f (s) есть линейный оператор действующий на N+1-мерную функцию h(s) с компонентами h_i(s), i=0,1,2,..N и имеющий область значений, включаемую в область значений оператора :

(7.70)

Принимая относительно области значений оператора (70), те же допущения, что и в цепочке равенств (10) для определения сопряженного оператора - , получим:

Отсюда следует, что значение сопряженного к оператора на элементе j(s₀) есть N+1 вектор, i-ая компонента которого:

(7.71)

Отсюда следует аналог (5.59) для характеристики :

(7.72)

i=0,1,…N.

Например, в том частном случае, когда оператор состоит в умножении на неотрицательную весовую функцию имеющую смысл оценки среднеквадратичной погрешности построения нулевого приближения[32], (72) перепишется:

(7.73)

Для случая, когда дополнительно и поле задано в конечном множестве точек - атомическая мера на , характеристика экстремального класса (72) примет другой частный вид:

(7.74)

Также как и для задачи в классе распределений плотности, дадим характеристику экстремального класса .Здесь для простоты доказательств используется оператор, определяющий поле на горизонтальной плоскости ( , и, кроме того, принимается, что область 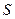совпадает с 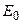. Возникающие несобственные интегралы, в этом случае, будем понимать в смысле главного значения. С этой целью рассмотрим задачу:

;

(7.75)

Далее мы намерены доказать, что необходимым условием для ее решения, при определенных ограничениях на служит:

, (7.76)

где непрерывная функция, одна и та же для всех .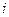

Это условие служит характеристикой экстремального класса .

Утверждение.Пусть решение задачи (75) существует, а уравнение (69) (первое уравнение в (75)) имеет решение на классе функций с представлением (76). Тогда, если и таковы, что:

1. множество непрерывных на 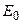функций , для которых

(7.77)

состоит только из нуля;

1. Для любой абсолютно и интегрируемой на 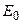функции :

, (7.78)

где сопряженный к оператор, а - непрерывная и абсолютно интегрируемая по любой комбинации переменных функция, а и не равно нулю тождественно[33], то решение уравнения в (75) на классе с представлением (76) есть решение задачи (75) и элемент экстремального класса .

Доказательство.

Пусть решение задачи (75) существует и есть . Это значит, что для всех вариаций , где принадлежит касательному к

.

Функционал принимает минимальное значение при . Касательное множество к в точке есть ядро оператора и состоит из таких , что:

(7. 79)

В сокращенной записи

.

Условие (79) эквивалентно:

(7.80)

Но поскольку и таковы, что для всех удовлетворяющих (80), функционал достигает минимума при , то должно быть решением задачи

(7.81)

(7.82)

Функция , вообще говоря, неизвестна. Это некоторая такая функция, которая будет доопределена после того, как будут найдены необходимые условия для искомого элемента за счет использования уравнения в (75), которое, в этом смысле заменяет (81).

Обозначим через Тогда от задачи (81-82) простой заменой переменных приходим к

Что в содержательных обозначениях переписывается:

(7.83)

Далее воспользуемся аппаратом теории двойственности для решения экстремальных задач. Поскольку линеен (относительно искомого ) и ограничен (из в ), а функционал в (83) есть норма в пространстве , то решение (83) существует, хотя может и быть неединственным. Для того, чтобы было решением, необходимо и достаточно, чтобы в сопряженном к пространстве нашелся функционал такой, что

; (7.84а)

; (7.84 б)

. (7.84в)

Все дальнейшее состоит в доказательстве того, что если имеет все компоненты, равные друг другу , то в условиях сформулированного утверждения, функционал , обладающий свойствами (84а-в), действительно существует. Отсюда и следует, что решение задачи (75) имеет вид (76) с

Из (84 в) следует, что принадлежит * - слабому замыканию (см. теорему у ядре в прил. 2.4) в множества ортогонального к . Но , где замыкание понимается, а * - слабой топологии. Но состоит из векторнозначных функций, компоненты которых есть:

. (7.85)

Действительно:

Тогда

(7.86)

Если в (86) все равны между собой, то (86) трансформируется в функционал на и соотношения (84а) и (84б) будут очевидным следствием, во-первых, всегда выполняющегося по определению равенства:

,

выражающего значение нормы через верхнюю грань значений функционалов, а во-вторых, плотности множества сумм функций с представлением (85) в единичном шаре пространства . Но в силу условия о нулевом ядре оператора (87) получаем, что множество значений оператора

(7.87)

плотно в .

Утверждение доказано.