Мат. ожид. И его св-ва

Мат. ожиданием дискретной сл. Вел. называют сумму произведений всех ее возможных значений на их вероятности.

Пусть случайная величина X может принимать только

значения xl x2, ..., хn, вероятности которых соответственно равны р1, р2, … рn. Тогда мат. ожидание М (X) случайной величины X определяется равенством М (X) = х1р1 + х2р2 + ... + хnpn.

Если дискретная случайная величина X принимает счетное множество возможных значений, то

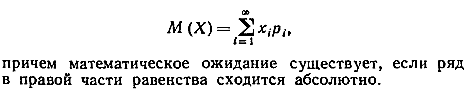
ат. Ожид. Непр. Сл. Вал. Х, знач. Кот. Лежат в промежутке [а,b]. Наз. Число М(Х), равное опред. Интегралу М(Х)= 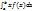, где f(х)-плотность распред. С.в.

Если возможные значения непр. С.в. Х заполняют всю числовую ось. То мат. Ожид. Равно несобст. Интегралу М(Х)= 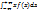. Причём несобст. Интеграл сход-ся абсолютно.

Свойства математического ожидания

1. Мат. ожидание постоянной величины равно самой постоянной: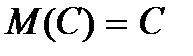

2. Постоянный множитель можно выносить за знак мат. ожидания:

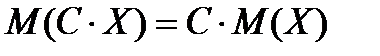
3. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий:

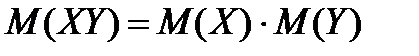
4. Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых:

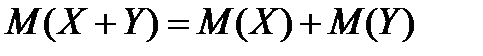
5.Математическое ожидание М (X) числа появлений события А в n независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытании: М (X) = nр.

Дисперсия и её св-ва. Ср.кв. отклонение

На практике часто требуется оценить рассеяние возможных значений случайной величины вокруг ее среднего значения. Такую оценку даёт дисперсия с.в.

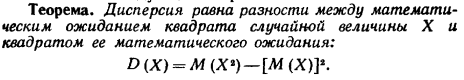
Св-ва:

1. Дисперсия постоянной величины

С равна нулю; D(С)=0

2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат: D(CX)=C² D(X)

3. Дисперсия суммы двух независимых

случайных величин равна сумме дисперсий этих величин: D(X+Y)=D(X)+D(Y)

4. Дисперсия разности двух независимых случайных величин равна сумме их дисперсий: D(X-Y)=D(X)+D(Y)

5.Дисперсия дискр. с.в., распред. по биноминальному з-ну: D(X)=npq

Дисперсия с.в. всегда неотриц. число.

Если непр. с.в. принримает знач. в числ. промежутке [a,b], то её дисп. вычисл.: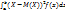

Если знач. непр. с.в. Х заполнит всю числ. ось, то диспер.вычисл. припомощи несобст. интеграла: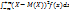

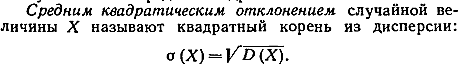
Мода и медиана непр. с.в.

Мода непр. с.в.Х наз. её возм. знач., в кот. плотность распред. f(х) имеет локальный максимум и обознач. М₀(Х).

Медианой непр. с.в. Х наз. такое её знач-е Ме(Х), для кот. выпол-ся рав-во: Р(Х<Ме(Х))=Р(Х>Ме(Х))=1/2

Т. обр. медиана делит мн-во значений непр. с.в. на 2 равновероятных мн-ва.

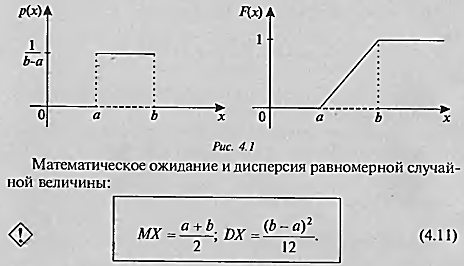
Равномерное распред. Биномин. распред.

Норм. Распред., осн. Хар-ки

Ф-цию распред. Опред. Через большую ф-лу Лапласа

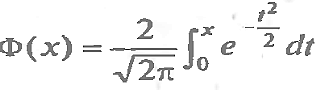
Её св-ва:

Ф(0)=0

Ф(-х)=-Ф(х)

Х>5, Ф(х)=1/2

Показ. З-н распред.. графики ф-ций и плотности распред., числовые хар-ки

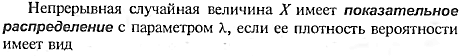
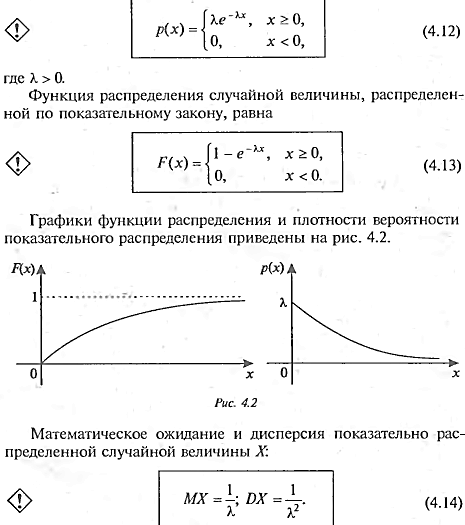
Числовые хар-ки