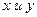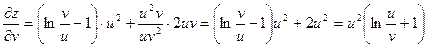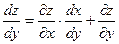Краткий справочник формул
Правила дифференцирования
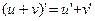 (1)
(1)
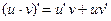 (2)
(2)
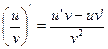 (3)
(3)
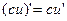 (4)
(4)
Таблица производных
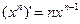 | 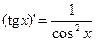 |
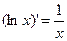 | 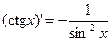 |
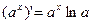 | 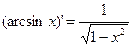 |
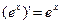 | 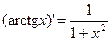 |
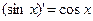 | 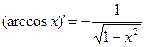 |
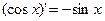 | 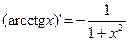 |
Правила вычисления частных производных
Частная производная функции 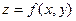 по
по 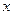 находится при дифференцировании
находится при дифференцировании 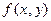 по
по 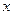 в предположения, что
в предположения, что 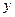 постоянная величина и обозначается
постоянная величина и обозначается 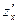 или
или 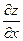 .
.
Частная производная функции 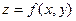 по
по 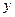 находится при дифференцировании
находится при дифференцировании
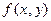 по
по 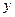 в предположения, что
в предположения, что 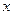 постоянная величина и обозначается
постоянная величина и обозначается 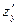 или
или 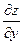 .
.
Полный дифференциал функции нескольких переменных
Полный дифференциал функции двух независимых переменных равен сумме произведений частных производных функции на дифференциалы соответствующих независимых переменных и обозначается 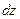 .
.
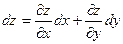
Приложение В
окончание
Формулы дифференцирования сложной функции

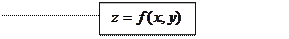

|
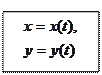 (5)
(5) 
|

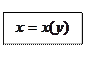 (6)
(6) 

|
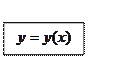 (7)
(7) 
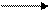
|
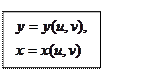 (8.1)
(8.1) (8.2)
Формулы дифференцирования неявной функции
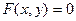
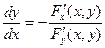 или
или 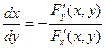 (9)
(9)
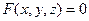 ,
, 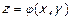
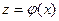
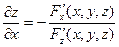 (10.1)
(10.1) 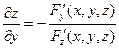 (10.2)
(10.2)
Приложение Г
Образцы выполнения типовых заданий
1 Найдите частные производные функции
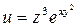
Обратите внимание, что данная функция является функцией трёх независимых переменных, поэтому находим три частные производные
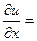 |
| 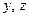 считаются постоянными величинами| =
считаются постоянными величинами| = 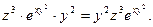
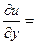 |
| 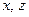 считаются постоянными величинами| =
считаются постоянными величинами| = 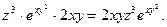
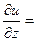 |
| 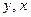 считаются постоянными величинами| =
считаются постоянными величинами| = 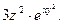
2Найдите полный дифференциал функции
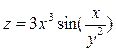
Воспользуемся формулой полного дифференциала 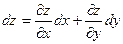
Найдем частные производные
Относительно независимой переменной х данная функция рассматривается как произведение двух функций, поэтому её частную производную по х находим по формуле (2)
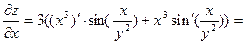
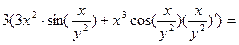
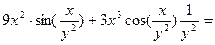
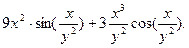
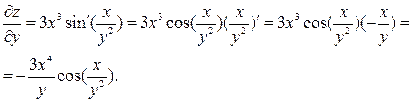
Подставим значения 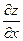 и
и 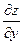 в формулу полного дифференциала
в формулу полного дифференциала
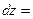
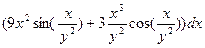
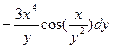
Приложение Г
продолжение
3 Найдите полную производную сложной функции
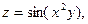 где
где 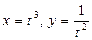
Полная производная находится по формуле:
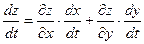
Найдём частные производные: 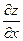 ,
, 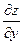
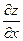 =
= 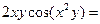 |
| 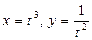 |=
|= 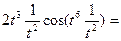
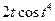
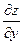 =
= 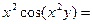 |
| 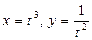 |=
|= 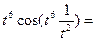
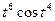
Найдём 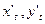 :
:
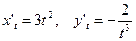
Подставим найденные значения в формулу 5 полной производной, упростим полученное выражение:
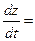
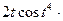
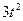 +
+ 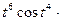
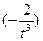 =
= 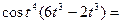
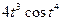

4Найдите полную производную сложной функции
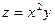 , где
, где 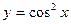
Полная производная находится по формуле:
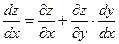
Найдём 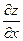 ,
, 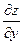
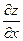 = 2xy,
= 2xy, 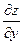
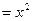
Найдём 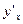
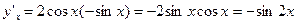
Найденные значения подставим в формулу
Приложение Г
продолжение
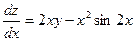 .
.
В полученное выражение 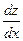 подставим значение
подставим значение 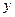
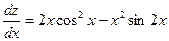 .
.
Замечание.Обратите внимание – результат дифференцирования записывается как функция независимой переменной.
5 Найдите производную сложной функции
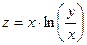 , где
, где 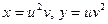
Частные производные функции находятся по формулам:
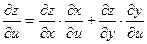 (8.1)
(8.1)
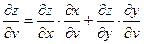 (8.2)
(8.2)
Найдём частные производные: 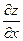 ,
, 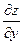
Относительно переменной x данная функция представлена произведением двух функций, воспользуемся правилом дифференцирования произведения ( формула 2)
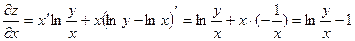
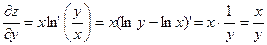
Найдём 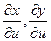
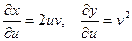
Найдённые значения подставим в формулу (8.1)
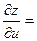
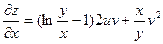
В полученное выражение 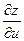 подставим значения
подставим значения 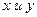
Приложение Г
продолжение
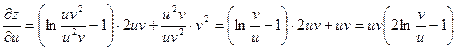
Найдём 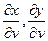
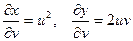
Найдённые значения подставим в формулу (8.2)
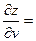
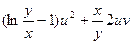
В полученное выражение 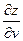 подставим значения
подставим значения