Числовые характеристики ДСВ
Корреляционный момент двумерной СВ 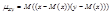
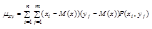
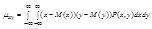
Теорема:корреляционный момент 2-ух независимых СВ xиyравен 0.
Док-во: если независимы x,y, то независимы x-M(x)и y-M(y). По св-ву мат. ожидания 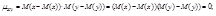 Коэффициент корреляции:
Коэффициент корреляции: 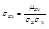 .
.
15.Неравенство Маркова. Неравенство Чебышева.
Пусть СВ X принимает только неотрицательные значения и у неё есть матем. Ожидание M(x), то какова бы ни была положительная величина ξ той же размерности, что и X, всегда выполняется 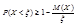 ;
;
Док-во: проведем док-во только для непрерывных СВ. P(X)=0,X<0; P(X)>=0,X>=0;
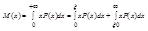 ;
;
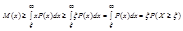 ;
;
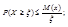
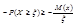 ;
; 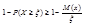 ;
; 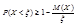 .
.
Неравенство Чебышева.
Какаво бы не было положительное число 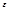 для любой СВ X, дисперсия которой конечна справедливо неравенство
для любой СВ X, дисперсия которой конечна справедливо неравенство 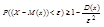 ;
;
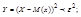
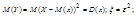
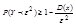 .
.
16. Т.Чебышева. Т.Бернули.
Последовательность чисел 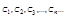 наз. равномерно ограниченной, если сущ. такая константа M ,
наз. равномерно ограниченной, если сущ. такая константа M , 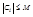 . Если
. Если 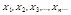 - последовательность попарно независимых СВ, у каждой из которых есть мат. ожидание
- последовательность попарно независимых СВ, у каждой из которых есть мат. ожидание 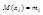 и
и 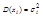 (дисперсии равномерно ограничены), то
(дисперсии равномерно ограничены), то 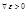 предел
предел 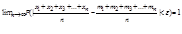 (6) -предел по вероятности.
(6) -предел по вероятности.
Док-во. По условию последовательность дисперсии равномерно ограниченна, т.е. 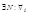 ,
, 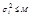 .
.
Рассмотрим вспомогательные СВ 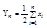 . У нее есть мат. ожидание
. У нее есть мат. ожидание 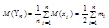
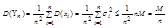
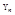 удовл. требованиям неравенства Чебышева. Применяя неравенство (6)
удовл. требованиям неравенства Чебышева. Применяя неравенство (6)
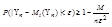 (8)
(8)
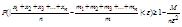 (9)
(9)
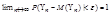
Следствие из теоремы : если 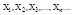 - последов независим. СВ имеющих одно и то же мат. ожидание
- последов независим. СВ имеющих одно и то же мат. ожидание 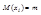 и
и 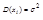 , то неравенство .(9). Примет вид
, то неравенство .(9). Примет вид 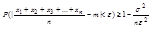 (10)
(10) 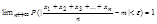
Следствие из теоремы важно на практике, если нужно измерить некоторую величину, истинное значение которой 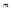 , проводят
, проводят 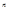 измерений этой величины. Если при измерениях отсутствуют системные ошибки, то
измерений этой величины. Если при измерениях отсутствуют системные ошибки, то 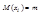 можно считать что дисперсии
можно считать что дисперсии 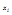 ограничены, тогда среднее арифм. значение рез-ов измерений с ростом n прибл. к истинному значепию измеряемой величины m . Можно положить, что
ограничены, тогда среднее арифм. значение рез-ов измерений с ростом n прибл. к истинному значепию измеряемой величины m . Можно положить, что 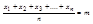 .
.
Т.Бернули
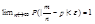 (1)
(1) 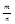 - относительная частота или частность (сходится к вер-ти)
- относительная частота или частность (сходится к вер-ти)
Док-во: Пусть 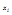 - число появления события A в первом испытании.
- число появления события A в первом испытании.
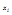 | |||
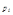 | q | p |
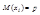 ,
, 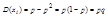
Мы находимся в условиях т.Чебышева
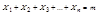 ;
; 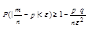
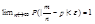
т.Бернули явл. статистическим определением вероятности.
17. Теорема Ляпунова:
Можно доказать что, если 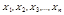 - нормально распределенные случайные величины, то их сумма
- нормально распределенные случайные величины, то их сумма 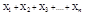 также норм. распред. СВ с мат. ожиданием
также норм. распред. СВ с мат. ожиданием 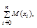
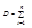 ,
, 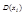
Обобщением явл. т. Ляпунова :
Пусть - независимые СВ, у каждой из которых мат. ожидание 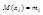
и 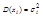 , абсолютный центральный момент третьего порядка
, абсолютный центральный момент третьего порядка 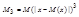 и выполняется
и выполняется 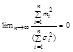 , .(3). то для суммы
, .(3). то для суммы 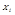 выполняется следующее
выполняется следующее 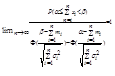 .(4).
.(4).
Следствие: если все 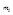 и
и 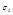 одинаковые, то
одинаковые, то 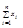 распределена асимптотически по нормальному закону.
распределена асимптотически по нормальному закону.
Физ. смысл условий, при кот. сумма 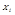 будет распространяться практически по норм закону, сост. в том, что удельный вес каждого слаг.
будет распространяться практически по норм закону, сост. в том, что удельный вес каждого слаг. 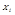 должен
должен 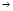 0 при увеличении числа слагаемых.
0 при увеличении числа слагаемых.
