Элементар.исход-соб-тия, кот явл-ся несовм. и единственно возм-ми. Классическое определение вероятности события. Случаи равновероятных исходов

События можно разделить на: достоверные (соб-тие, кот. В дан.испытании обязат-но произойдет), невозможные (соб-тие, кот не м.произойти в дан.исп-нии), случайные (соб-тие, кот. в дан.исп-нии м.произойти, а м. и не пройзойти). В свою очередь случайные делятся на: совместные, несовместные, равновозможные и единственновозмож. события. Два события называются совместными в данном опыте, если появление одного из них не исключает появления другого. Два события называются несовместными в данном опыте, если они не могут произойти вместе при одном и том же испытании. Несколько событий называются несовместными, если они попарно несовместны. Равновозм.-если в результате исп-ния ни одно из соб-тий не явл-ся более возможным, чем другие. Единственновозм.-если в рез-те исп-ния появление хотя бы одного из события будет достоверным.

3. Случайным в теории вероятностей называют событие, которое при данном испытании, в данном опыте может либо произойти, либо не произойти и для которого имеется определенная вероятность его наступления.

Случайные события делятся на: несовместные, равновозможные и единственновозмож. события. Несовместные -если соб-тия не могут произойти вместе при одном и том же испытании. Равновозм.-если в результате исп-ния ни одно из соб-тий не явл-ся более возможным, чем другие. Единственновозм.-если в рез-те исп-ния появление хотя бы одного из события будет достоверным.

Полная группа событий

Множество попарно несовместных событий называют полной группой событий, если при любом исходе случайного эксперимента непременно наступает одно из событий, входящих в это множество.

Вероятность случайного события 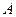, обозначаемая 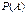– числовая мера степени возможности появления данного события при определенных условиях. При этом всегда .

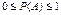Событие называется достоверным, если в результате опыта оно обязательно произойдет. Его вероятность равна единице.

Событие называется невозможным, если в результате опыта оно не может произойти; его вероятность равна нулю.

Суммой нескольких событий называется событие, заключающееся в появлении хотя бы одного из них. Несколько событий 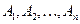называются несовместимыми в данном опыте, если никакие два из них не могут появиться одновременно.

Если в каком-то опыте может произойти либо событие 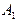, либо событие 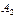, то событие 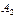называют противоположным событию 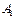, и обозначают 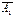, считая что:

.

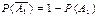Теорема. Сумма вероятностей событий полной группы 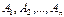равна единице:

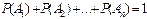
5. Эл-ты комбинаторики: сочетание- наборы, составленные из n разл-х эл-в по m, кот отлич-ся хотя бы 1 эл-м 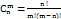Размещение- наборы,сост-е из n различных эл-в по m эл-м,кот отлич.либо составом, либо порядком 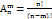Перестановки- наборы,сост-е из одних и тех же n разл-х эл-в, и отлич. только порядком их распред-я. 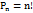, 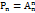Решение большинства комбинаторных задач основано на применении двух основных правил – правила суммы и правила произведения.

Правило суммы: Если элемент А можно выбрать т способами, а элемент В – п
способами (причем, ни один из способов выбора элемента А не совпадает со способом
выбора элемента В), то выбрать А или В можно т + п способами. Правило произведения: Если элемент А можно выбрать т способами и после каждого такого выбора элемент В можно выбрать п, то выбрать упорядоченную пару (А,В) можно тхп способами.

Элементар.исход-соб-тия, кот явл-ся несовм. и единственно возм-ми. Классическое определение вероятности события. Случаи равновероятных исходов

Классическое определение вероятности связано с определением благоприятствующего исхода. Исход называется благоприятствующим данному событию, если его появление влечет за собой наступление этого события. Вероятность события 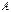равна отношению числа равновозможных благоприятствующих элементарных исходов к общему числу всех равновозможных и единственно возможных элементарных исходов данного испытания:

,

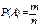где 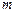– число благоприятствующих событию 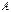исходов;

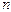– общее число возможных исходов.

Из определения вероятности события 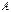следует, что 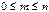, поэтому всегда выполняются неравенства 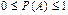, т.е. вероятность любого события есть неотрицательное число, не превышающее единицы.

Если 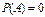, то событие 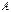невозможное.

Если 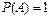, то событие 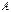достоверное.

Равновозможные элементарные события являются равновероятными, т.е. обладают одной и той же вероятностью.