Свойства двойного интеграла

Задача о вычислении объема цилиндрического тела. Двойной интеграл.

Определенный интеграл 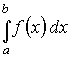функции одной переменной обычно вводится на основе решения задачи о вычислении площади криволинейной трапеции.

Аналогично этому вводится двойной (определенный) интеграл: .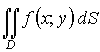

Рассмотрим задачу о приближенном вычислении объема цилиндрического тела (рис. 2.1), ограниченного снизу плоской областью D, расположенной на плоскости Оxy, сверху - поверхностью, заданной уравнением z=f(x;y), (x;y) 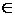D, где функция f(x;y) - непрерывна и положительна на D; а сбоку - цилиндрической поверхностью с образующими, параллельными оси Оz, проходящими через всю границу Г области D.

Объем V этого тела будем находить приближенно, произвольно разбив его вертикальными плоскостями на большее число n мелких вертикальных "частей" (как режут картофель на мелкие длинные кусочки).

Одна из таких частей выделена на рис. 2.1. Ее объем ΔV_i можно приближено посчитать как объем призмы (считая, что ее "крыша" - плоская): ΔV_i≈ΔS_i·h_i, где ΔS_i - площадь основания Δσ_i, h_i - средняя высота, т. е.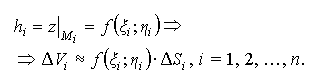

Тогда объем V всего цилиндрического тела: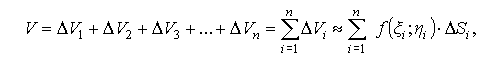

то есть получена интегральная сумма.

Далее: при n 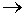∞ и при уменьшении всех площадей ΔS_i до нуля Получим: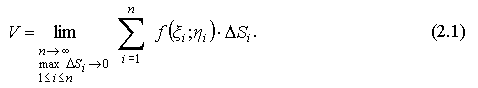

Получен предел (2.1) интегральной суммы, который обозначается через 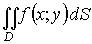и называется двойным интегралом от функции f(x;y) по области D.

Замечание:

в этой задаче предполагалось, что подынтегральная функция положительна и непрерывна на D.

В общем же случае имеем:

Определение

Пусть f(x;y), x 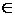D, - произвольная функция на D. Разобьем область D произвольным образом на части Δσ₁, Δσ₂,..., Δσ_n. Их площади обозначим соответственно ΔS₁, ΔS₂,..., ΔS_n. Внутри каждой Δσ_i произвольно выберем точку M_i(ξ_i;η_i) и составим интегральную сумму:

Если существует предел: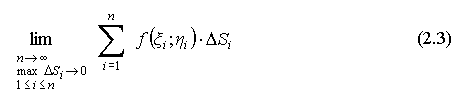

интегральной суммы, причем, этот предел не зависит от способов разбиения D на части Δσ₁, Δσ₂,..., Δσ_n, а также от произвола в выборе точек M_i(ξ_i;η_i),
то этот предел обозначается через 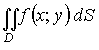и называется двойным интегралом от функции f(x;y) по области D. При этом функция f(x;y) называется интегрируемой по области D.

Теорема

Если f(x;y) непрерывна на D, то она интегрируема по D.

Без доказательства.

Определение

Если подынтегральная функция f(x;y) непрерывна на D, то двойной интеграл 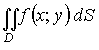называется собственным двойным интегралом, а если внутри D или на ее границе Г есть точки разрыва f(x;y), то двойной интеграл называется несобственным (он может существовать, а может и не существовать, но эта тема в данном пособии не рассматривается).

В дальнейшем полагаем, что все рассматриваемые в этой главе функции интегрируемы по D.

Свойства двойного интеграла

1. Геометрический смысл двойного интеграла.

Если z=f(x;y) - положительна на D, то интеграл равен объему цилиндрического тела, изображенного на (рис.2.1):

2. 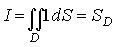- площадь области D.

Доказательство

Здесь 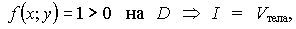, которое ограничено: снизу - областью D на плоскости Оxy, сверху - поверхностью z=f(x;y), но z=1 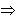это цилиндрическое тело есть прямой цилиндр высоты Н = 1 с основанием D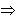 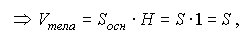что и требовалось доказать.

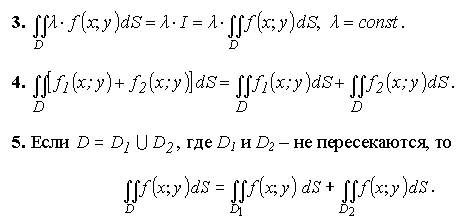
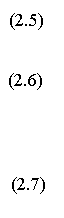
6. Оценка двойного интеграла снизу и сверху: если 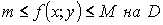, то где S - площадь области D.

Теорема

(О среднем значении для двойного интеграла).

Если f(x;y) - непрерывна на замкнутой области D, то существует 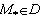- некая "средняя" точка области:

ДоказательствоЕсли f(x;y) непрерывна на D, то существуют наименьшее m и наибольшее М значения функции f(x;y), т.е. 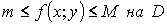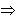по свойству 6 имеем: 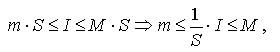то есть число I/S находится между m и М.

Но непрерывная функция f(x;y) принимает все промежуточные от m до М значения 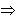существует точка 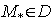: 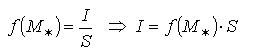,и теорема 2.2 доказана.

******************