Приведем порядок (алгоритм) решения любой задачи (проблемы)
1. Ставится ФПЗ (физическая постановка задачи). Дано – найти. Цель.
2. Проводится обзор работ, патентно-информационный поиск (ПИП). Наброски математической модели.
3. Ставится МПЗ (математическая постановка задачи). Проводится анализ МПЗ.
4. Выбор и обоснование метода решения. АВМ, ЭЦВМ, эксперимент – что есть в наличии.
5. Решение задачи.
6. Анализ полученного решения
7. Выводы и рекомендации.
1.4 Стационарная теплопроводность
1.4.1. Теплопроводность плоской однослойной стенки.
Рассмотрим наиболее простые случаи.
а) физическая постановка задачи. Пусть дана неограниченная плоская однослойная стенка толщиной d (Рис.1).
Рис. 1.4 Теплопроводность в плоской стенке
Пусть коэффициент теплопроводности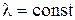 
. Известны температуры на левой поверхности Тп.1, а на правой – Тп.2, которые не изменяются со временем. Внутренние источники теплоты отсутствуют, т.е. qV= 0. Температуры T вдоль осей OY и OZ=const. Тогда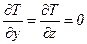 
Задача: Требуется найти распределение температур по сечению T(x) и тепловой поток q через стенку.
б) математическая постановка: для расчета процесса теплопроводности следует использовать уравнение (7) в декартовой системе координат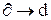 
, т.к. стенка плоская. Учтем, что температуры неизменны во времени, т.е.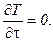 
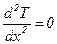; (15)
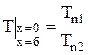; (16), (17)
Решение (15):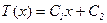 
; (18)
, 
; 
, 
, 
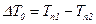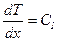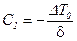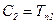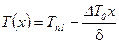, (19)
Анализ полученного решения.
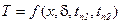. Температура согласно (19) меняется вдоль стенки по линейному закону.
Весьма удобно представить решение в безразмерном виде: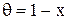 
, где 
, 
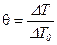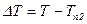, т.е.отсчет ведем от наименьшей температуры.
3) Тепловой поток согласно закону Фурье: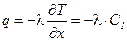 
,
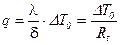, (20)
где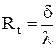 
м2К/Вт – термическое сопротивление плоской стенки.
2а)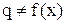 
другой вид (2)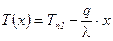 
2б) Полное количество теплоты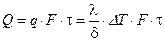 
, Дж
Если учесть зависимость коэффициента теплопроводности, например,
3) по линейному закону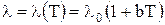 
, то решением будет
, 
,
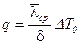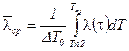Распределение температур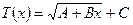 
– уже будет не прямая, а кривая линия.
1.4.2. Теплопроводность плоской многослойной стенки.
Дано: число слоев m, режим стационарный
Известны: Tn1 и Tn(нар) (Рис. 1.5)
Определить: q и Tпов.внутр.
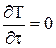, пользуемся случаем, что 
.
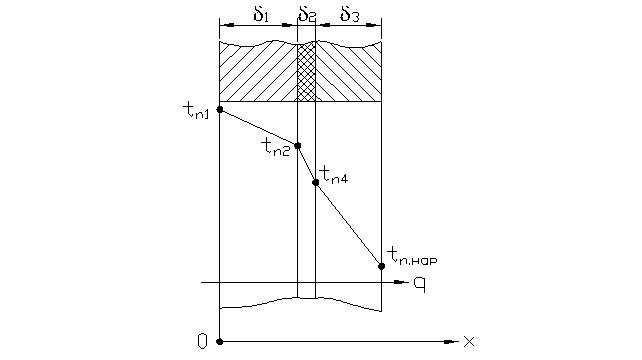
Рис. 1.5. Теплопроводность плоской многослойной стенки
В местах контакта: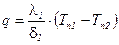 
, 
, 
………………………………………………………….
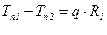
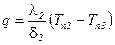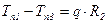
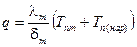
Определив DT – (температурные напоры) и сложив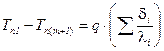 
.
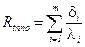– полное термическое сопротивление многослойной стенки равное сумме Rt всех слоев.
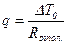, зная q, вернемся к Tni : 
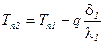и т.д.
.
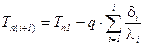1.4.6. Теплопередача через плоскую однослойную стенку
ОПРЕДЕЛЕНИЕ. Передача тепла от одной более горячей среды (жидкости или газа) к другой холодной , через разделяющую их одно или многослойную стенку любой формы называется теплопередачей.
Известны, в отличие от предыдущей задачи, температуры не на поверхности стенки, а температуры окружающей среды Тж.1 слева и Тж.2 – справа и коэффициенты теплоотдачи a1 и a2. Требуется найти поле температур и тепловой поток через стенку.
Рис. 1.6 Теплопередача через плоскую стенку.
, 
, 
,
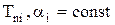
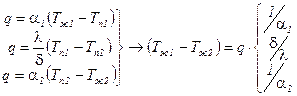
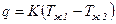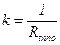К – коэффициент теплопередачи, характеризует интенсивность передачи теплоты от одной жидкости к другой через разделяющую их стенку.
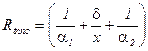- полное термическое сопротивление, м2 К/Вт;
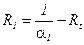горячей среды;
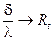, теплопроводности стенки; 
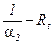- холодной жидкости.
Зная q, найдем температуры: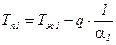 
;
.
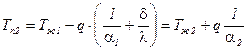1.4.4. Теплопередача через плоскую многослойную стенку
Даны: температуры горячей и холодной сред, толщины, коэффициенты теплопроводности и теплоотдачи (Рис.1.7).
Найти: поле температур и тепловой поток через многослойную стенку.
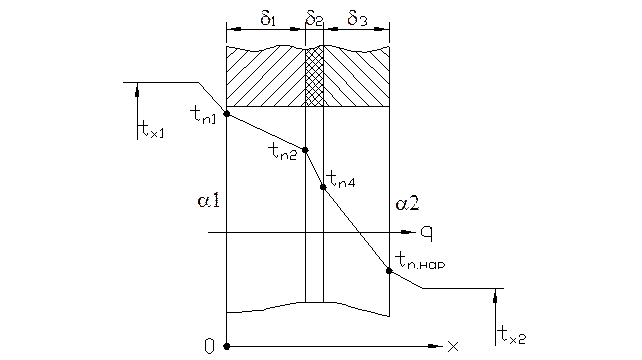
Рис. 1.7 Теплопередача через плоскую многослойную стенку
,
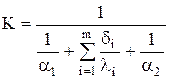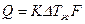– Основное уравнение теплопередачи. 
DT – температурный напор, F – поверхность нагрева; тепло соприкасающаяся поверхность, та поверхность, которую пронизывает тепловой поток.
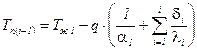
Res.1. Уравнения для случая (а) получаются из (б) как частные случаи при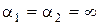 
.
ГУ IIр.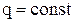 
, и 
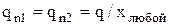, то 
;
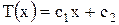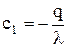, а с2 – любое, т.е. любая прямая удовлетворяет q.
Для нахождения единственного решения, нужно задать дополнительное условие, например Тпояв.
1.4.5. Теплопроводность цилиндрической стенки
а) ГУ Iр.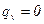 
, 
, 
, 
.
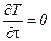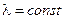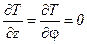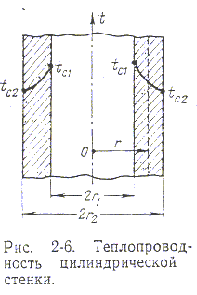
Здесь нужно брать дифференциальное уравнение теплопроводности в цилиндрической системе координат.
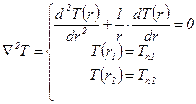
Уравнение теплопроводности решаем путем введения подстановки: u=dT/dr. 
® 
; 
, 
.
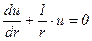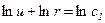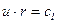
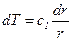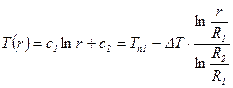Здесь температура вдоль стенки изменяется по логарифмическому закону.
, 
,
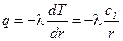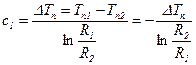Здесь, в отличие от плоской стенки, тепловой поток зависит от радиуса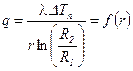 
,
, 
, 
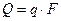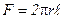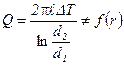
Опять неудобно, нужно сделать чтобы было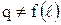 
. Введем понятие линейной плотности теплового потока
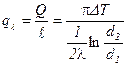, Вт/м.
В знаменателе стоит термическое сопротивление цилиндрической стенки, мК/Вт.
1.4.6. Теплопроводность многослойной цилиндрической стенки
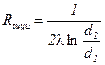, сразу 
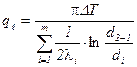, Вт/м.
Рис. 1.9. Теплопроводность цилиндрической многослойной стенки
1.4.7. Теплопередача через цилиндрическую однослойную стенку
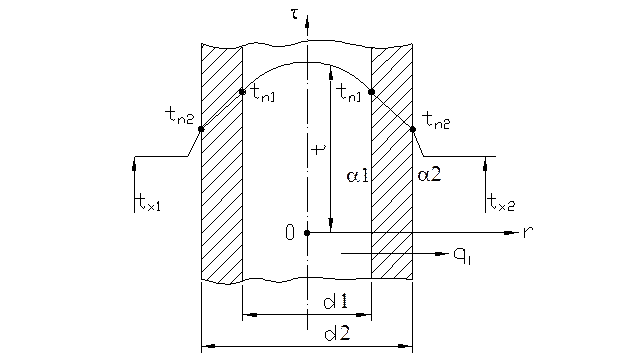
Рис. 1.10. Теплопередача через однослойную цилиндрическую стенку
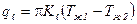, где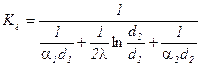 
.
Кi – линейный коэффициент теплопередачи Вт/м×К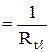 
.
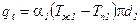
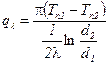
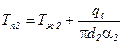
Анализ: в сравнении с плоской стенкой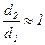 
, или бцил. стен.<< d2 ,
то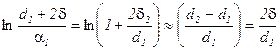 
и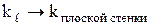 
1.4.8. Теплопередача через многослойную цилиндрическую стенку
Много слойка , m-слоев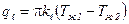 
, 
.
.
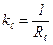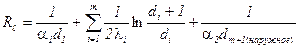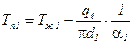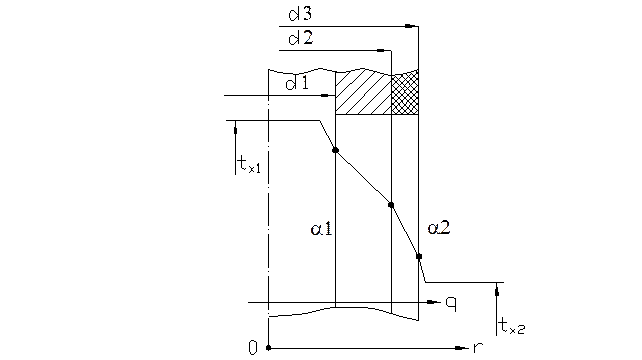
Рис. 1.11 Теплопередача через многослойную цилиндрическую стенку
1.4.9. Критический диаметр тепловой изоляции
ОПРЕДЕЛЕНГИЕ.Тепловая изоляция - это всякое покрытие горячей поверхности, которое способствует снижению потерь теплоты в окружающую среду.
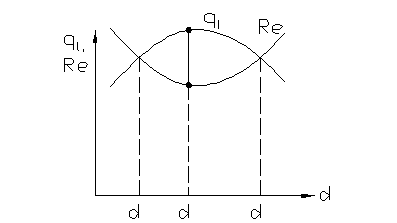
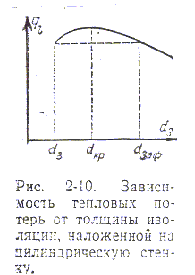
Рис. 1.12. Зависимость тепловых потерь от толщины изоляции, наложенной на цилиндрическую стенку
Термическое сопротивление такой стенки
.
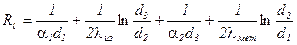Здесь оказалось, что количество не всегда пропорционально качеству.
Исследуем функцию сопротивления на экстремум (Рис. 1.12). Для этого берем производную по диаметру изоляции и приравниваем ее нулю.
Окончательно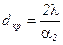 
. 
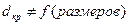
Если будет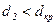 
то изоляция не эффективна. Должно быть: 
,
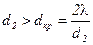Для других стенок, кроме плоской, можно получить аналогичные решения.
( т.к.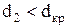 
, то шлаковату применять нельзя. Для нашей задачи
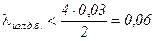Вт/мК.)
1.4.10. Теплопередача через шаровую стенку
Для шара: Поле температур T(r)= C1 - C2 /r . Тепловой поток:
, 
, 
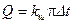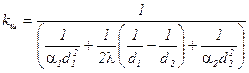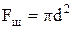
1.4.11. Теплопередача через стенки неправильной формы:
; 
; 
;
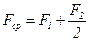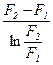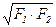F1 – внутренняя, F2 – внешняя
; 
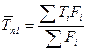–усредненное по поверхности
