Точечное оценивание параметров распределения

Пусть требуется изучить некот кол-ый признак генер-ой сов-ти. Допустим, что из теор-их соображений удалось устан-ть, какое именно распр-ие имеет признак и необ-мо оценить параметры, кот оно опр-ся. Напр, если изуч признак распр-н в генеР-й сов-ти норм, то нужно оценить матема-ое ожидание и среднее квадр-кое откл-ие; если признак имеет распределение Пуассона – то необх оценить параметр l.

Обычно имеются лишь д-ые выборки, напр значения кол-го признака 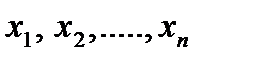, полученные в рез-те n незав-х набл-ий. Рассм-ая 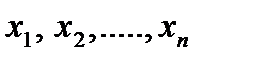как незав-ые случ величины 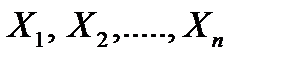можно сказать, что найти стат-ую оценку неизв-го параметра теор-го распред-я – это значит найти ф-цию от наблюд-х случ величин, кот дает прибл-ое значение оц-го параметра. Напр, для оценки матем-го ожид-я норм распред-я роль ф-ции выполняет среднее арифм-ое:

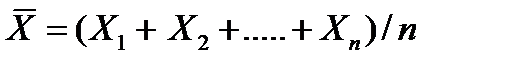
Для того чтобы стат-ие оценки давали корректные приближ-я оцениваемых парам-в, они должны удовл-ть некот треб-м, среди кот важн-ми явл требования несмещенности и состоятельности оценки.

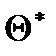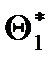Пусть – стат оценка неизвестного параметра теоретического распред-я. Пусть по выборке объема n найдена оценка . Повторим опыт, т.е. извлечем из генер-й сов-ти другую выборку того же объема и по ее д-м получим другую оценку 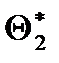. Повторяя опыт многократно, получим различные числа 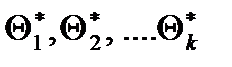. Оценку 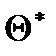можно рассм-ть, как случайную величину, а числа 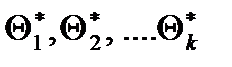– как ее возможные значения.

Несмещенной наз стат-ую оценку 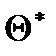, мат-ое ожидание кот равно оцениваемому параметру при любом объеме выборки .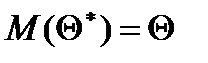

Смещенной наз оценку, не удовлетв-ую этому условию.

Эффективной наз стат оценку, которая, при заданном объеме выборки n, имеет наименьшую возможную дисперсию.

Состоятельной наз стат оценка, кот при n®¥ стремится по вер-ти к оцениваемому параметру.

39. ИНТЕРВАЛЬНОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЯ.

До сих пор мы рассматривали точечные оценки, т.е. такие оценки, которые определяются одним числом. При выборке малого объема точечная оценка может значительно отличаться от оцениваемого параметра, что приводит к грубым ошибкам. В связи с этим при небольшом объеме выборки пользуются интервальными оценками.

Интервальной называют оценку, определяющуюся двумя числами – концами интервала. Пусть найденная по данным выборки статистическая характеристика 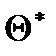служит оценкой неизвестного параметра . Очевидно, 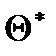тем точнее определяет параметр , чем меньше абсолютная величина разности 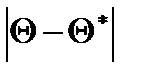. Другими словами, есл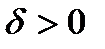и и 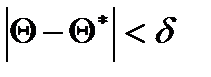, то чем меньше d, тем точнее оценка. Таким образом, положительное число d характеризует точность оценки.