Нагрев тел конечных размеров

Геометрически длинный прямоугольный стержень можно рас­сматривать как тело, образованное пересечением двух, а в случае параллелепипеда – трех взаимно перпендикулярных неограничен­ных пластин с размерами 2d_x × 2d_y × 2d_z.

В [2, 3] доказывается, что общее решение для тел конечных размеров можно представить как произведение безразмерных темпе­ратур, так называемая теорема “О перемножении решений”. Тогда для параллелепипеда с началом координат в центре, получим

q(X, Y, Z, Fо) = q_x × q_y × q_z , (90)

где q_x = (t (x,t) – t_ж)/Dt₀ = F_x(X, Bi_x, Fо_x); q_y = (t (y,t) – t_ж )/Dt₀ =F_y(Y, Bi_y, Fо_y);

q_z = (t (z,t) – t_ж)/Dt₀ = F_z(Z, Bi_z, Fо_z); X = x / d_x; Y = y / d_y; Z = z / d_z;

Bi_x = ad_x / l; Bi_y = ad_y / l; Bi_z = ad_z / l - числа Био для соответст­вующих пластин;

Fо_x = at / d_x²; Fо_y = at / d_y²; Fо_z = at / d_z² – числа Фурье.

Аналогично для средней температуры:

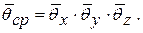
Для длинного прямоугольного стержня (начало координат на оси симметрии и поверхности узкой грани):

q(X, Y, Fо) = q_x × q_y . (91)

Расчет безразмерных температур q_х, q_у, q_z производится по формулам (8… 73), полученным выше.

АНАЛИТИЧЕСКИЕ РАСЧЁТЫ ОГРАНИЧЕНИЙ НА ТЕХНОЛОГИЧЕСКИЕ ПАРАМЕТРЫ ПРИ ФОРСИРОВАННЫХ НАГРЕВАХ СТАЛЬНЫХ ТЕЛ

В работах [75…79] приведены номограммы В.С. Старикова для определения допустимой температуры греющей среды при форсированном нагреве слябов в виде неограниченной пластины, цилиндра или шара. На рис. 1 в качестве примера приведена одна из таких номограмм для шаровых тел [138]. Номограмма многофункцио-нальна т.к. позволяет определить время достижения максимального перепада температур по сечению тела и самое главное, наибольшую температуру печной среды при тепловой обработке тел с учётом допустимых и разрушающих термических напряжений.

Расчёты на ЭВМ процессов нагрева тел затруднены необходимостью использования графиков назначении режимов нагрева. Целью данной работы является аналитическое определение ограничений на технологические параметры.

Изложение материалов исследования.

При выводе расчётных соотношений будем следовать методике, изложенной в работах [10,16]. Сначала подробно покажем ход расчёта нагрева плоских тел.

Неограниченная пластина. В случае конвективного нагрева пластины в печи с постоянной температурой греющей среды t_c относительные температуры определяются соотношениями:

на поверхности

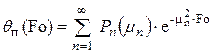,(1)

В центре

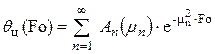,(2)

и среднемассовая

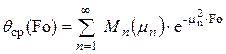,(3)

где 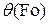=(t(τ)–t_c)/Dt₀; Dt₀= t₀– t_c; t_{0 ­} – начальная температура тела, °С;

Fо= aτ/R₀²;

Вi=αR₀/λ – число Био; 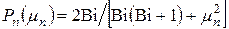– тепловая амплитуда; 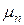– собственные числа, определяемые уравнением:

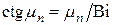. (4)

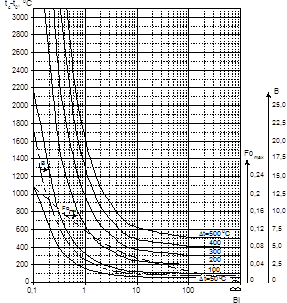
Рисунок 5.1 – Номограмма для определения температуры греющей среды при тепловой обработке стальных тел шарообразной формы с учетом максимальных перепадов температур по сечению

Вычитая из первого уравнения (1) второе, получим относительный перепад температур

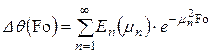, (5)

где .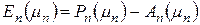

Зависимость перепада температур 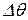от времени носит коло-колообразный характер с максимумом в точкеFо = Fо_mах. Дифференцируя уравнение (5) по времени, приравнивая производную нулю и используя два члена суммы ряда, получим формулу для расчёта максимального времени:

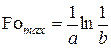, (6)

где ; ; .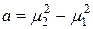

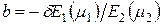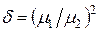Подставляя Fо_mах в уравнение (5), получим максимальный перепад температур с учётом двух членов ряда:

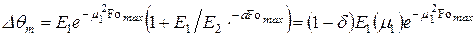. (7)

При выводе (7) было учтено, что согласно уравнению (6): .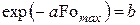

Если из технологических соображений известна допустимая в процессе нагрева разность температур Dt_доп между поверхностью и центром тела, то из уравнения (7) можно найти сначала максимальную начальную разность температур

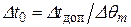, (8)

а затем максимальную допустимую температуру греющей среды

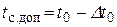. (9)

Наибольшую и основную трудность при практических расчётах по уравнениям (1)…(7) представляет определение по соотношению (4) бесчисленного множества корней. В работе [13] приведена общая формула для расчета первого корня для тел простой формы

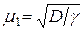, (10)

где 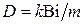; 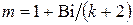_­ – коэффициент термической массивности; ;

;

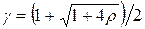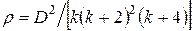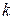– коэффициент геометрической формы, равный 1 _­ – для пластины, 2 _­ – цилиндра и 3 _­ – шара.

Для определения приближенных значений остальных корней следует различать два характерных случая нагрева – при больших и малых числах Био [12].

При малых числах Био (Bi < 3)

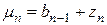(11)

где ; ; ; ;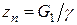

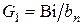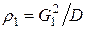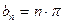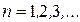
При больших ( )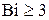

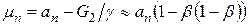, (12)

где 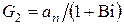; ; 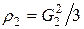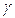– см. уравнение (10); ; .

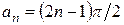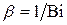При выводе (12) было учтено, что при малых аргументах .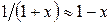

Неограниченный цилиндр. Для расчета температур на поверхно-сти, в центре и среднемассовой используются уравнения (1)…(3), в которых начальные тепловые амплитуды находятся по следующим формулам:

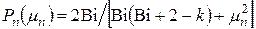, (13)

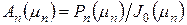, (14)

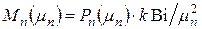. (15)

Вместо (4) характеристическое уравнение станет

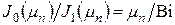, (16)

где 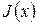– функция Бесселя первого рода.

Первый корень уравнения (16) в случае 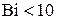рассчитывается по уравнению (10) при коэффициенте формы 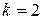. Остальные корни согласно [14] при малых числах Био

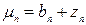, (17)

где 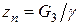; ; 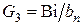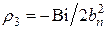: 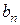– корни уравнения (16) при 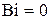, т.е. 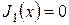, согласно справочным данным 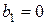; ; 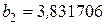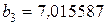и т.д.

При больших числах Био ( ):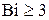

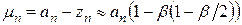, (18)

где ; ; ;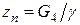

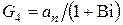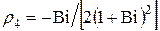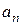– корни уравнения (16) при 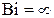, т.е. нули функции ,

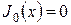а именно: 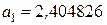; 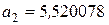и т.д.

Шар. Величины 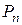, 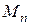вычисляются по уравнениям (13), (15) и первый корень по (10) при коэффициенте формы .

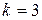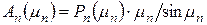(19)

Вместо (4) характеристическое уравнение будет 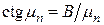, (20)

где .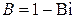

Согласно работе [15] корни уравнения (20) соответственно при малых числах Био по формуле (17) в которой ;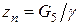

; ; .

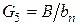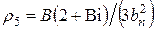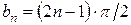При больших числах Био 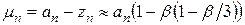, (21)

где 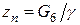; ; ; .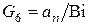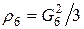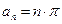