По теме практического занятия
Матрицей размера 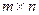 называется прямоугольная таблица чисел, содержащая m строк и n столбцов:
называется прямоугольная таблица чисел, содержащая m строк и n столбцов:
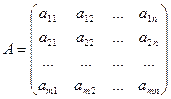 .
.
Если число столбцов матрицы n равно числу её строк m, то матрицу называют квадратной матрицей порядка n: 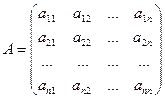
Элементы 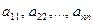 квадратной матрицы порядка n образуют её главную диагональ, а элементы
квадратной матрицы порядка n образуют её главную диагональ, а элементы 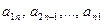 – побочную диагональ.
– побочную диагональ.
Квадратная матрица называется диагональной, если все её элементы, расположенные вне главной диагонали, равны нулю: 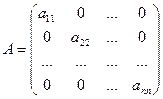 .
.
Диагональная матрица называется единичной, если все её элементы, расположенные на главной диагонали, равны единице: 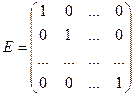 .
.
Матрица 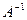 называется обратной для квадратной матрицы А, если
называется обратной для квадратной матрицы А, если 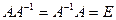 .
.
Квадратная матрица имеет обратную тогда и только тогда, когда её определитель не равен нулю.
Алгоритм составления обратной матрицы:
1. Вычислить определитель матрицы 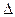 .
.
2. Вычислить алгебраическое дополнение каждого элемента.
3. Найти обратную матрицу по формуле 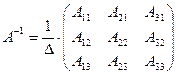 , где
, где 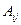 - алгебраическое дополнение элемента
- алгебраическое дополнение элемента 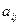 матрицы А.
матрицы А.
Выделим произвольно t-строк и t-столбцов в матрице А размера 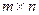 ,
, 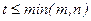 . Определитель порядка t, составленный из элементов стоящих на пересечении выделенных t-строк и t-столбцов называется порожденным матрицей А.
. Определитель порядка t, составленный из элементов стоящих на пересечении выделенных t-строк и t-столбцов называется порожденным матрицей А.
Рангом матрицы называется натуральное число равное наибольшему из порядков определителей, отличных от нуля, среди порожденных данной матрицей.
Если 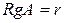 , значит существует определитель порядка
, значит существует определитель порядка 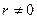 ; все определители порядка больше чем r обращаются в нуль.
; все определители порядка больше чем r обращаются в нуль.
Ранг матрицы А не изменится, если:
- строки заменить столбцами (транспонировать);
- поменять местами два столбца (строки);
- умножить каждый элемент столбца на одно и тоже число, отличное от нуля.
- сложить два столбца (строки).
Перечисленные действия называют элементарными преобразованиями матриц.
Матрицы, полученные одна из другой путём элементарных преобразований, называются эквивалентными (обозначаются 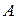 ~ В).
~ В).
Чтобы вычислить ранг матрицы А, путём элементарных преобразований сводим её к ступенчатому виду (в частности, к треугольному).
Для отыскания ранга матрицы надо:
1) элементарными преобразованиями превратить матрицу в трапецеидальную;
2) подсчитать число ненулевых строк в трапецеидальной матрице.
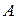 ~
~ 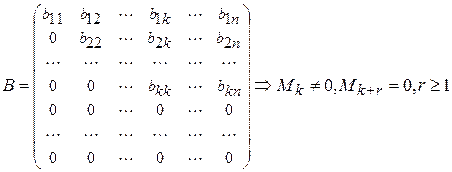 ,
,
rang A = rang B = k.
Вопросы для закрепления теоретического материала к практическому занятию:
1. Что такое матрица?
2. Какие матрицы называются равными?
3. Какая матрица называется квадратной?
4. Что называется главной диагональю?
5. Что называется побочной диагональю?
6. Какая матрица называется диагональной?
7. Какая матрица называется единичной?
8. Как найти определитель 2-го, 3-го порядка?
9. Как найти обратную матрицу?
10. Что называется рангом матрицы?
11. Как вычислить ранг матрицы?
