Экспоненциальное распределение

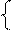f(x)= 0, x<0

le^-l, x³0

l>0, l - const.

Экспоненциальное распределение описывает различные поведения процессов.

x

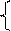F(x) = ò f(t)dt = 0, x<0

-¥ 1 - e^-lx, x³0 M[x] = D[x] = 1\l

Распределение Хи – квадрат.

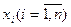
Система независимых случайных величин, которые распределены по нормальному закону распределения.

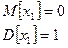
Если получаем случайную величину 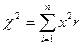, то говорят, что случайная величина - распределена по закону Хи – квадрат с n степенями свободы.

В случае если на заданную систему случайных величин наложено r связи, тогда число степеней свободы будет равна k = n – r.

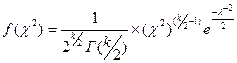
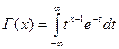
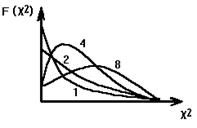
k = ¥, f(c²) – нормальное.

k Þ 20 ¸ 25

Статистическое оценивание последовательности чисел.

Первичная проверка генератора случайных (псевдослучайных) чисел.

Пример:

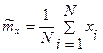
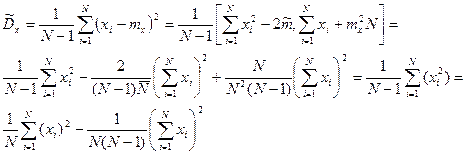
Проверка качества последовательностей псевдослучайных чисел.

Качество последовательности случайных чисел – это соответствие последовательности требуемых законов, то есть функция распределения на основе опытов должна соответствовать функции теоретической, или гистограмма.

1) соответствие F*(x)~F(x)

f*(x)~f(x)

2) независимость элементов последовательности друг от друга

3) случайность последовательности

4) отсутствие периода

N

N≤0.1 T_max

Каждый из четырех критерий проверяется по своей методике:

1)Соответствие F*(x),F(x)

1.1тест по критерию согласия

• Критерий Хи – квадрат
• Критерий Колмогорова

1.2 Точечные характеристики

Использование доверительных интервалов соответствующих заданной последовательности теории равномерных чисел

1.3 проверка /*распределение по равномерному закону */

1.3.1. тест пар

1.3.2. тест колебаний

1.3.3. тест многомерной равномерности (многомерности)

1.3.4. тест “наибольшее из t”

2)критерий качества - независимость элементов последовательности

k_t – на основе теста автокорреляции

3)Случайность

3.1. тест серий

3.2. тест монотонности

4) отсутствие периода

Тест апериодичности.

Рассмотрим тесты

1. соответствие заданному закону распределения

T¹. F*(x), f (x)

Эмпирически (на практике) F*(x),f*(x)

Алгоритм построения гистограммы

1 шаг – последовательность чисел

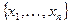на 1 шаге max, min значения из данной последовательности

2 шаг ранжирование либо по возрастанию, либо по убыванию (обычно по возрастанию)

3 шаг разбиение интервала, на котором распределены значения (x₁,…,x_n) на равные интервалы

4 шаг подсчет числа попаданий S_i элементов последовательности в каждый из интервалов.

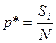
Указанные данные могут быть выведены либо табличным способом, либо гистограммой.

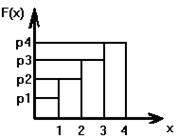Посчитаем на каждом шаге суммарную вероятность положительных элементов на каждом из интервалов.