Случайные погрешности прямых измерений
Прямые измерения одной и той же величины дают после многократных повторений процесса измерения совокупность случайных величин, состоящую из конечного число элементов (n → ∞) а1, а2, ......, an.
Истинное значение измеряемой величины никогда неизвестно. Обозначим его через а(без индекса). Тогда истинная абсолютная погрешность любого i - того измерения равна
| Δаi = |аср - ai|. | (1) |
Для серии n измерений получим
| Δа1 = |аср – a1|, Δа2 = |аср – a2|, ………………. Δаn = |аср – an|. | (2) |
cовокупность абсолютных погрешностей Δаi, содержащая n - ное число элементов (n не ∞). Величины Δаi могут быть положительными, отрицательными и равными нулю.
Следует отметить, что для совокупности абсолютных погрешностей выполняются два утверждения:
1) при большем числе измерений случайные погрешности одинакового значения, но разного знака встречаются одинаково часто.
2) большие (по абсолютной величине) погрешности встречаются реже, чем малые, то есть вероятность появления погрешности уменьшается с ростом значения погрешности.
Очевидно, что обе совокупности - результаты серии прямых измерений величины аi и совокупность абсолютных погрешностей Δаi описываются нормальным распределением Гаусса для конечного, но достаточно большого числа n измерений. Для совокупности n случайных измерений аi величины а, среднее равно истинному значению величины а. Для распределения абсолютных погрешностей это среднее равно нулю. Покажем это:
| a1 = а - Δa1 а2 = а - Δа2 …………………. аn = а - Δаn. | (3) |
Суммируя левую и правую части равенств, получим
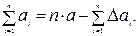 | (4) |
Если обозначить среднеарифметическую величину 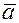
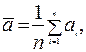 то то 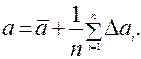 | (5) |
При n достаточно большом
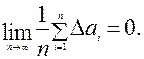 | (6) |
При ограниченном числе измерений теория вероятностей даёт вместо теоретических, величии Δаi и σ конкретные «измеренные» величины абсолютной ошибки Δа серии измерений при заданной надежности α и дисперсии σ.
Обычно в эксперименте производится небольшое число измерений (n ≤ 20) и распределение Гаусса становится несправедливым. Для оценки границ доверительного интервала в этом случае вводится новый коэффициент tα,n. Этот коэффициент был предложен в 1908 году английским математиком B.C. Госсетом, публиковавшим свои работы под псевдонимом "Стьюдент" - студент. Задавая надежность α по таблицам Стьюдента, определим коэффициент tα,n, который необходим для вычисления абсолютной погрешности Δа серии измерений. Коэффициенты Стьюдента tα больше единицы, это значит, что доверительный интервал увеличивается в несколько раз, чтобы при малом числе измерений получить требуемую надёжность результата. Распределение Стьюдента переходит в распределение Гаусса и tα → 1 при n → ∞.
В теории погрешностей в качестве единицы ширины доверительного интервала выбрана так называемая средняя квадратичная погрешность результата измерений:
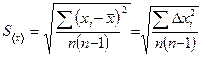 | (7) |
Было предложено в случае небольшого числа измерений (именно так обстоит дело в учебных лабораториях) вычислять полуширину доверительного интервала по формуле:
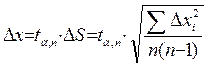 | (8) |
где ta,n - некоторое, зависящее от a и n число, называемое коэффициентом Стьюдента. Зависимость ta,n от n понятна: чем больше n, тем меньше 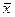 отличается от истинного значения, и тем меньше будет доверительный интервал, точнее результат измерения, а значит меньше ta,n.
отличается от истинного значения, и тем меньше будет доверительный интервал, точнее результат измерения, а значит меньше ta,n.
