Инструкция по выполнению практического занятия №3
1. Прочитайте краткие теоретические и учебно-методические материалы по теме практического занятия.
2. Устно ответьте на вопросы для закрепления теоретического материала к практическому занятию.
3. Выберите свой вариант (задания для практического занятия) и выполните задание.
4. Внимательно прочитайте условие задачи. Определите, какое правило для вычисления данного предела необходимо использовать.
5. При выполнении первого задания используйте правило вычисления предела многочлена.
6. Для выполнения второго задания нужно использовать правило нахождения предела дробно-рациональной функции в точке, принадлежащей области определения функции.
7. При выполнении третьего задания используйте связь между бесконечно малыми и бесконечно большими величинами (если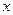 
- величина бесконечно большая, то обратная ей величина 
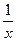является бесконечно малой) и определение предела бесконечно малой величины (предел бесконечно малой величины равен нулю).
8. Для выполнения четвертого, пятого и шестого заданий воспользуйтесь правилом раскрытия неопределенностей вида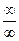 
(необходимо числитель и знаменатель разделить на самую высокую входящую в знаменатель степень 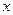) и связью между бесконечно малыми и бесконечно большими величинами.
9. В заданиях семь, восемь и девять функции представляют собой дробь, пределы числителя и знаменателя которых равны нулю. Чтобы раскрыть неопределенность вида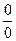 
, необходимо числитель (а в восьмом примере и знаменатель) разложить на множители.
10. Чтобы раскрыть неопределенность вида 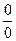в десятом задании, следует избавиться от иррациональности в числителе или знаменателе. Для этого умножьте и числитель, и знаменатель на сопряженное выражение (например, для 
сопряженным будет выражение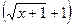 
. Затем преобразуйте выражение и перейдите к пределу.
11. В задании одиннадцать имеем неопределенность вида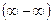 
. Необходимо привести дроби к общему знаменателю, произвести заданное действие и сократить на общий множитель числитель и знаменатель. Вычислить предел преобразованного выражения.
12. При выполнении двенадцатого задания неопределенность вида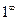 
раскрывается с использованием второго замечательного предела.
13. В задании тринадцать преобразуйте функцию, предел которой необходимо вычислить, и приведите ее к виду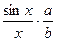 
. Затем перейдите к пределу, используя первый замечательный предел и теоремы о пределах.
14. Проверьте правильность решения заданий.
15. Убедившись, что задания решены правильно на черновике, аккуратно спишите их в чистовик.