Анализ сетей массового обслуживания с блокировками. Метод вероятностных графов Ли

Рассмотренный выше марковский подход к анализу сетей массового обслуживания позволяет рассчитать вероятности состояний для сетей, состоящих из узлов, каждый из которых есть СМО типа M/M/m. При этом предполагается, что каждый узел содержит бесконечный накопитель и все заявки будут обслужены через некоторое время. Другой постановкой задачи является анализ сети с узлами, в которых может быть СМО с блокировкой заявок. Часто такими СМО выступают коммутационные схемы, имеющие конечные пучки соединительных линий. Другой моделью являются сети с множественным доступом к фиксированному числу каналов. Рассмотрим в качестве примера (рис.2) подключение сельского абонента С через абонентскую линию с блокиратором к сельской АТС в пункте В, которая в свою очередь имеет два канала связи с АТС в пункте А. Требуется определить вероятность блокировки звонка абоненту С из пункта А. Поставим в соответствие рассматриваемой сети так называемый вероятностный граф (граф Ли), с вершинами А, В и С и ребрами a,b,c соответствующими потокам заявок. Будем называть их далее звеньями, и параметризовать значениями некоторых вероятностей их занятия.

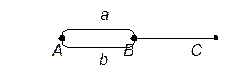
Рис. 2 Подключение абонента С с абонентом А через АТС в пункте В.

Метод Ли состоит в том, что вероятность блокировки пути между любыми вершинами графа может быть рассчитана как вероятность совместного занятия всех соединяющих эти вершины звеньев в предположении, что вероятности занятия каждого из звеньев независимы.

Вероятность совместного занятия может быть рассчитана с помощью известных теорем теории вероятностей для сложных событий.

Обозначим вероятности занятия звеньев a,b,c соответственно .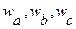

Вероятности того, что звено свободно можно найти как

.

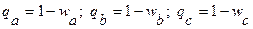Вероятность блокировки пути АВ будет определяться как совместная вероятность занятости a и b: .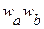

Вероятность свободности этого пути: .

Общая вероятность свободности пути АС будет

.

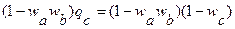Тогда вероятность блокировки пути АС будет

.

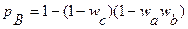Граф, рассмотренный здесь, относится к классу параллельно-последовательных. Для расчета вероятностей таких графов в общем случае применяются простые правила, сведенные ниже в таблицу:

Вероятность занятости (блокировки)	wi=1-qi
Вероятность свободности (неблокированности)	qi=1-wi
Параллельное включение звеньев	w=w1w2w i…wn
Последовательное включение звеньев	q=q1q2qi…qn

Бывают случаи, когда граф сети не сводится к параллельно-последовательным схемам. Например, мостиковый граф (рис. 3)

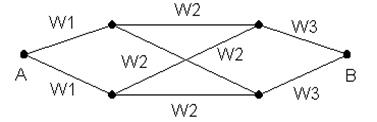
Рис. 3 Мостиковый граф.

Для такого графа можно получить вероятность блокировки пути АВ в виде

.

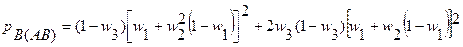Графы типа приведенных выше часто встречаются при анализе многозвенных коммутационных схем. Там они имеют более сложный вид, например как на рис. 4 и 5.

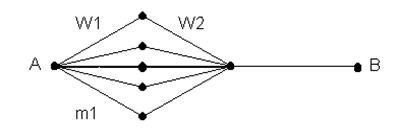
Рис. 4 Пример параллельно – последовательного графа.

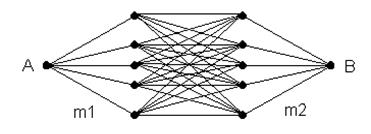
Рис. 5 Пример параллельно – последовательного графа.

Для этих графов можно получить явные выражения для вероятности блокировки пути АВ

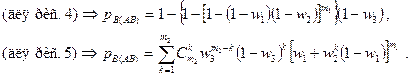
В том случае, если граф получается слишком сложным, можно пользоваться методом оценочных графов. Строится граф оценки сверху путем разделения вершин и отбрасывания ребер для упрощения расчета и граф оценки снизу путем объединения части вершин. Рассчитываются вероятности блокировки для оценочных графов, которые и будут служить соответственно верхней и нижней границей, между которыми и будет лежать значение вероятности блокировки для исходного графа.