Математическая модель транспортной задачи

Одной из характерных задач ЛП является так называемая транспортная задача. Она возникает при разработке наиболее рациональных способов и путей транспортирования товаров, устранение встречных, повторных и слишком дальних перевозок. А это сокращает время продвижения товаров и уменьшает затраты предприятий, осуществляющих процессы снабжения сырьём, топливом, оборудованием и т.д. Различают два вида транспортных задач: по критерию стоимости и по критерию времени.

Первая задача является частным случаем задачи ЛП и может быть решена симплексным методом, однако наличие большого числа переменных и ограничений делает вычисление громоздким. Поэтому для решения этих задач разработан специальный метод, позволяющий быстрее и проще находить оптимальный план решения задачи.

Сформулируем транспортную задачу.

Определить оптимальный план перевозок некоторого однородного груза от m поставщиков A₁, A₂, …A_m к n потребителям B₁, B₂, …B_n, причём стоимость перевозки 1 ед. груза (тариф) из пункта A_i, в пункт B_j равна c_ij.

Введём обозначения:

a_i – запасы грузы в пункте отправления A_i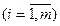

b_j – величина заказа на этот груз в пункте назначения B_j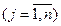

c_ij – тарифы перевозок из A_i в B_j

x_ij – количество груза, доставленного из A_i в B_j.

В зависимости от соотношения между суммарными запасами груза и суммарными потребностями в нём транспортные задачи могут быть закрытыми и открытыми.

Определение. Транспортная задача называется закрытой, если 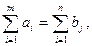в противном случае задача называется открытой.

Условия транспортной задачи обычно задаются распределительной таблицей.

Математическая модель закрытой задачи имеет вид:

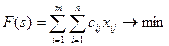
при ограничениях

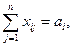т.е. от каждого поставщика будет вывезен весь груз в объёме данного ресурса,

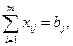т.е. каждому потребителю будет доставлен весь груз в объеме его потребности,

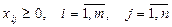
и условии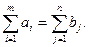

Оптимальным решением этой задачи является матрица 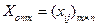, удовлетворяющая системе ограничений и доставляющая минимум целевой функции.

Всякую открытую транспортную задачу можно привести к закрытой с помощью добавления фиктивного поставщика или фиктивного потребителя, принимая тарифы по этим направлениям равными 0.

Основные этапы решения транспортной задачи:

а) нахождение исходного опорного решения,

b) проверка этого решения на оптимальность,

c) переход от одного опорного решения к другому.

5.2 Нахождение исходного опорного плана.

Существует несколько способов нахождения исходного опорного плана: метод северо-западного угла, метод минимальной стоимости.

Опишем применение этих методов на примере транспортной закрытой задачи, заданной распределительной таблицей:

Табл.13

bj ai

По методу северо-западного угла вначале получают значение перевозки x₁₁, которая расположена в северо-западной клетке матрицы перевозок. Причём x₁₁ присваивается максимально возможное значение, 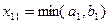. После этого вычеркивают соответствующий столбец (строку), так как остальные перевозки из этого столбца (строки) должны быть равны 0. Если a₁=b₁, должны быть вычеркнуты и первый столбец, и первая строка. Затем корректируют запасы (потребности) невычеркнутой строки (столбца), и все повторяется для северо-западной клетки оставшейся матрицы. Исходное опорное решение представляется таблицей:

Табл. 14

bj ai
	34	–3	–2
	13	45	–4
	–1	22	103

Значение целевой функции

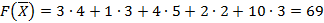
По методу минимальной стоимости вначале заполняется перевозка x_ij с минимальной стоимостью c_ij. Если минимальных стоимостей несколько, выбирается произвольная переменная. Выбранной перевозке присваивается максимально возможное значение, x_ij=min(a_i,b_j). Затем вычеркивается соответствующий столбец (строка), корректируется потребность (запас) не вычеркнутого столбца( строки) и всё повторяется сначала. Тогда исходное решение представляется таблицей:

Табл. 15

bj ai
	–4	–3	32
	–3	–5	54
	41	62	23

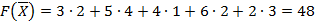
Очевидно, что полученные затраты на перевозки по плану, составленному методом наименьшей стоимости, ниже затрат по плану, составленному методом северо-западного угла.

Следовательно, второй план перевозок ближе к оптимальному.